Figure shows part of a circuit. If l = 5A and is decreasing at a constant rate of 103A/s then VB−VA is
15 V
20 V
10 V
5 V
The correct Answer is:A
To solve the problem, we need to find the potential difference VB−VA in the given circuit. We will use the concepts of Ohm's law, Kirchhoff's voltage law, and the formula for the induced voltage across an inductor.
1. Identify the Components:
The circuit consists of a resistor (1 ohm), a voltage source (15 volts), and an inductor (5 millihenry). The current I is given as 5 A and is decreasing at a rate of dIdt=−103A/s.
2. Apply Kirchhoff's Voltage Law:
According to Kirchhoff's voltage law, the sum of the potential differences around any closed loop in a circuit must equal zero. We can write the voltage drop from point A to point B as:
VA−I⋅R−V+L⋅dIdt=VB
where:
- VA is the voltage at point A,
- I is the current (5 A),
- R is the resistance (1 ohm),
- V is the voltage source (15 volts),
- L is the inductance (5 millihenry = 5×10−3H),
- dIdt is the rate of change of current.
3. Substitute the Known Values:
Plugging in the known values into the equation:
VA−5⋅1−15+5×10−3⋅(−103)=VB
4. Calculate Each Term:
- The voltage drop across the resistor: 5⋅1=5V
- The voltage source: 15V
- The induced voltage across the inductor:
5×10−3⋅(−103)=−5V
5. Combine the Terms:
Now substituting these values into the equation:
VA−5−15−5=VB
Simplifying gives:
VA−25=VB
6. Find the Potential Difference:
Rearranging the equation to find VB−VA:
VB−VA=−25V
Therefore, the potential difference VB−VA is:
VB−VA=15V
Final Answer:
VB−VA=15V
The circuit consists of a resistor (1 ohm), a voltage source (15 volts), and an inductor (5 millihenry). The current I is given as 5 A and is decreasing at a rate of dIdt=−103A/s.
According to Kirchhoff's voltage law, the sum of the potential differences around any closed loop in a circuit must equal zero. We can write the voltage drop from point A to point B as:
VA−I⋅R−V+L⋅dIdt=VB
where:
- VA is the voltage at point A,
- I is the current (5 A),
- R is the resistance (1 ohm),
- V is the voltage source (15 volts),
- L is the inductance (5 millihenry = 5×10−3H),
- dIdt is the rate of change of current.
Plugging in the known values into the equation:
VA−5⋅1−15+5×10−3⋅(−103)=VB
- The voltage drop across the resistor: 5⋅1=5V
- The voltage source: 15V
- The induced voltage across the inductor:
5×10−3⋅(−103)=−5V
Now substituting these values into the equation:
VA−5−15−5=VB
Simplifying gives:
VA−25=VB
Rearranging the equation to find VB−VA:
VB−VA=−25V
Therefore, the potential difference VB−VA is:
VB−VA=15V
VB−VA=15V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - C)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - D)
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
55 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
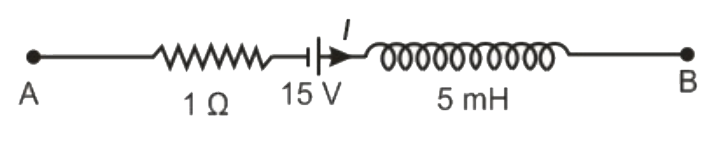
The network shown in the figure is part of a complete circuit. If at a certain instant, the current I is 5A and is decreasing at a rate 103A/s then VB−VA is
View SolutionThe network shown in figure is a part of a complete circuit. If at a certain instant, the current i is 4 A and is increasing at a rate of 103A/S. ThenVB−VA will be
View SolutionIn the given circuit, current I is 2A and it is decreasing at the rate of 103AS−1.Then VB−VA is
_PHY_E06_148_Q01.png)
View SolutionFigure shows a part of a circuit.Find the rate of change as shown.

View SolutionThe network shown in the figure is part of a complete cirtain instant the current (I) is 5A and is decreasing at a rate of 103 A s−1, then the value of VB−BA is
View SolutionThe network shows in Fig is part of a complate circuit. If at a certain instant the current (I) is 5A, and is decreasing at a rate of 105As−1 then VB−VA=−V.

View SolutionFigure shows a part of a bigger circuit. The capacity of the capacitor is 6mF and is desaesing at the constate rate 0.5mFs−1. The potential difference across the capacitor at the shows moment is changing as follows:
dVdt=2Vs−1, d2Vdt2=12VS−2
The current in the 4Ω resistor is decreasing at the rate of 1mAs−1. What is the potential difference (in mV) across the inductor at this moment?

View SolutionIn the circuit diagram shown, R=10ω,L=5mH,E=10 V and i=1A. The current is decreasing at the reate of 103A/S. Then (VA−VB)at this instant is :

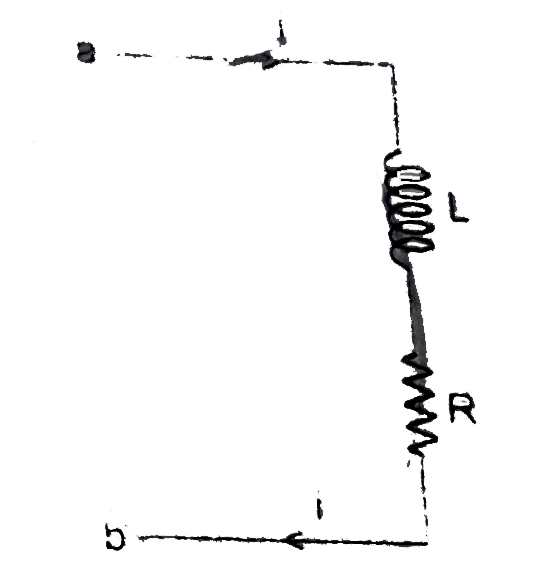
View SolutionWhen the current in the portion of the circuit shown in the figure is 2A and increasing at the rate of 1A/s,the measured potential difference Va−Vb=8V.However when the current is 2A and decreasing at the rate of 1A/s, the measured potential difference Va−Vb=4V.The values of R and L are:
View SolutionIf the instantaneous change on the capacitor is 100μC and current through the circuit is decreasing at the rate of 2×103 As then potential difference VA−VB is equal to
_PHY_E06_046_Q01.png)
View Solution
