Define angular velocity(u). Derive v=rω.
Text Solution
Angular velocity (ω) :
The rate of change of angular displacement of a body is called angular velocity. i.e., ω=dθdt
Derivation of v=rω
Consider a rigid body be moving with unform speed (v)along the circumberence of a circle of radius r. Let the body be displaced from A to B in a small interval of time Δt making an angle Δθ at the centre. Let the linear displacement be Δx from A to B.
From the property, length of arc = radius × angle
Δx=rΔθ
This equation is divided by Δt, and taking
Limit Δt→0 on both sides. We get LtΔt→0ΔxΔt=rLtΔt→0ΔθΔt
But LtΔt→0ΔxΔt=vandLtΔt→0ΔθΔt=ω∴v=rω.
|
Similar Questions
Knowledge Check
In the figure shown the end A of the rod of length L is being pushed down parallel to the inclined surface with a velocity =v let the velocity of end B=u and the angular velocity of the rod = ω then
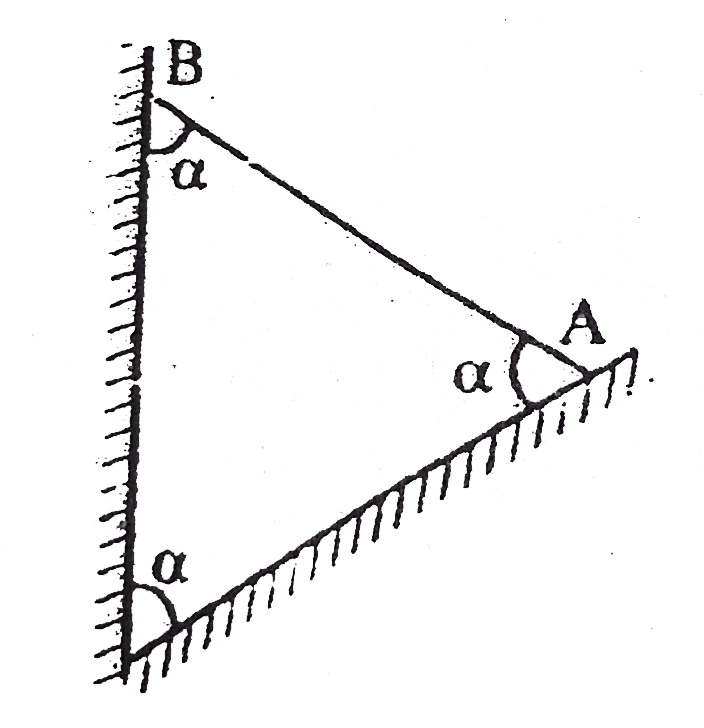 Au=vcosα (upward)Bu=v (downwards)Cω=vsinα/LDω=2vsinα/L
Au=vcosα (upward)Bu=v (downwards)Cω=vsinα/LDω=2vsinα/LRelation between Linear velocity (v) and Angular velocity (ω)
Av=rωBω=vωCr=vωDv=ωr
Define angular velocity and angular acceleration.
View SolutionIn a uniforme circular motion, the linear velocity of a particle
View Solution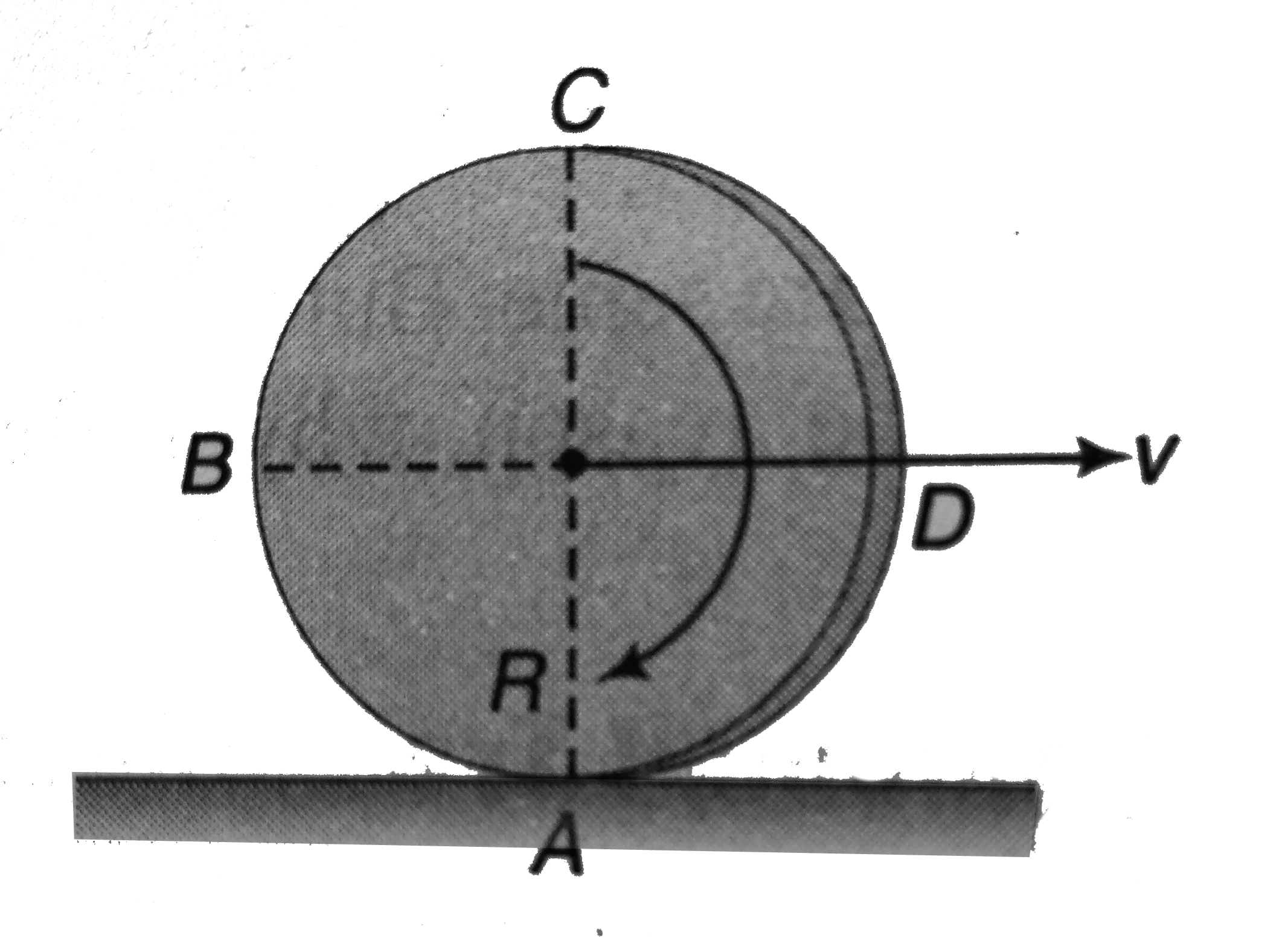
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View Solution
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View SolutionEstablish a relation between angular momentum and moment of inertia of a rigid body.
View SolutionDefine angular momentum, write its unit and obtain relation for angular momentum in terms of moment of inertia and angular velocity.
View Solution
