Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill upto a particular comon height. Is the force exerted by the water on the base of the vessel the same in the two cases ? If so, why do the vessels filled with water to that same height given different readings on a weighing scale ?

Since the pressure depends upon the height of water column and the height of the water column in the two vessels of different shapes is the same, hence there will be same pressure due to water on the base of each vessel. As the base area of each vessel is same, hence there will be equal force acting on the two base areas due to water pressure. The water exerts force on the walls os the vessel also. In case, the walls of the vessel are not perpendicular to base, the force exerted by water on the walls has a net non-zero vertical component which is more in first vessel than that of second vessel. That is why, the two vessels filled with water to same vertical height show different readings on a weighing machine.
Similar Questions
Two vessels have the same base area but differnent shapes. The first vessel takes twice the vloume of water that the second vessel requires to fill up to a paricular common height . Is the force exerted by water on the base of the vessel the same in the two case? If so, why do the vessels filled with water to that same height give different reading on a weighting scale ?
View SolutionTwo vessels have the same base area but differnent shapes. The first vessel takes twice the vloume of water that the second vessel requires to fill up to a paricular common height . Is the force exerted by water on the base of the vessel the same in the two case? If so, why do the vessels filled with water to that same height give different reading on a weighting scale ?
View Solution
Knowledge Check
The height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is
 A13ρbh2gcosθB12bh2ρgC12ρbh2gsecθDZero
A13ρbh2gcosθB12bh2ρgC12ρbh2gsecθDZeroA vessel consists of two plane mirrors at angles (as shown in figure). The vessel is filled with water. The total deviation in incident ray is
 A0∘B90∘C180∘DNone of these
A0∘B90∘C180∘DNone of theseTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
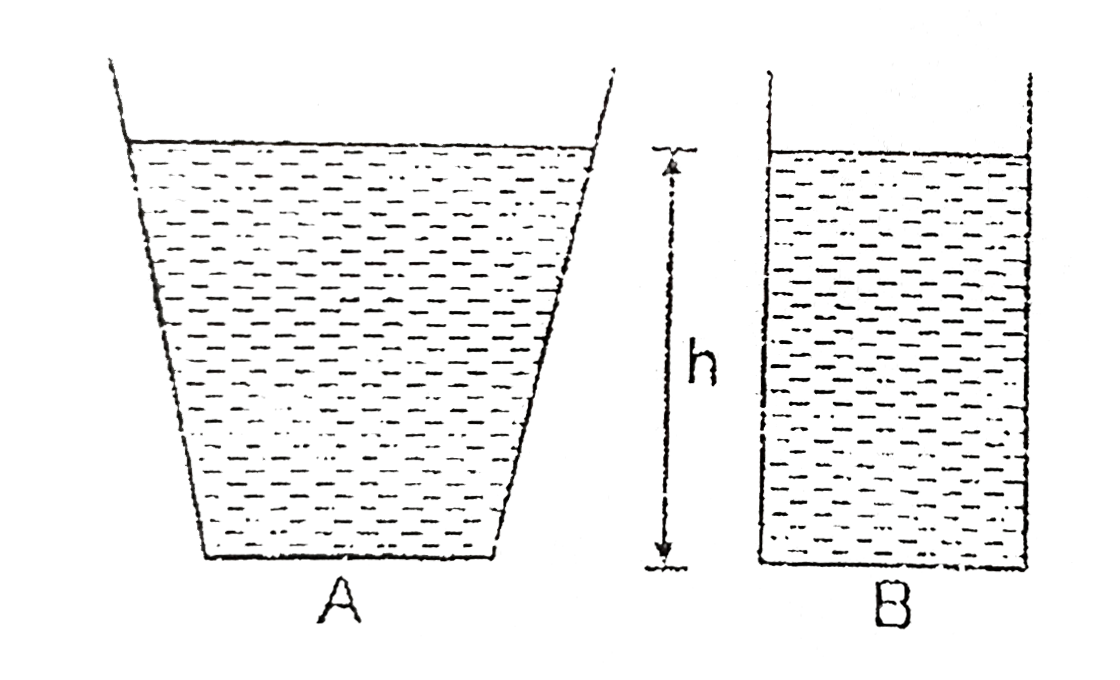 AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WB
AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WB
Two identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same ?
View SolutionTwo identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same .
View SolutionThe height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is

View SolutionTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then

View SolutionTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then

View Solution
