The filament of a bulb takes a current 100 mA when potential difference across it is 0-2 V. When the potential difference across it becomes 1.0 V, the current becomes 400 mA. Calculate the resistance of the filament in each case and account for the difference.
To solve the problem, we will calculate the resistance of the filament in two different cases using Ohm's Law, which states that R=VI.
Step 1: Calculate Resistance for Case 1
- Given:
- Current I1=100mA=100×10−3A=0.1A
- Voltage V1=0.2V
- Using Ohm's Law:
R1=V1I1=0.2V0.1A=2Ω
Step 2: Calculate Resistance for Case 2
- Given:
- Current I2=400mA=400×10−3A=0.4A
- Voltage V2=1.0V
- Using Ohm's Law:
R2=V2I2=1.0V0.4A=2.5Ω
Step 3: Compare the Resistances
- We have calculated:
- R1=2Ω
- R2=2.5Ω
Step 4: Account for the Difference
- The resistance R2 is greater than R1. This difference can be attributed to the temperature effect on the filament:
- As the current increases, the filament heats up, which increases its resistance. This is a common behavior in materials, particularly in metals, where resistance increases with temperature.
Final Answer
- The resistance of the filament at 0.2 V is 2Ω and at 1.0 V is 2.5Ω. The increase in resistance is due to the increase in temperature of the filament when a higher current flows through it.
---
- Given:
- Current I1=100mA=100×10−3A=0.1A
- Voltage V1=0.2V
R1=V1I1=0.2V0.1A=2Ω
- Given:
- Current I2=400mA=400×10−3A=0.4A
- Voltage V2=1.0V
R2=V2I2=1.0V0.4A=2.5Ω
- We have calculated:
- R1=2Ω
- R2=2.5Ω
- The resistance R2 is greater than R1. This difference can be attributed to the temperature effect on the filament:
- As the current increases, the filament heats up, which increases its resistance. This is a common behavior in materials, particularly in metals, where resistance increases with temperature.
- The resistance of the filament at 0.2 V is 2Ω and at 1.0 V is 2.5Ω. The increase in resistance is due to the increase in temperature of the filament when a higher current flows through it.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B)
15 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (MULTIPLE CHOICE TYPE)
3 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(A) ( MULTIPLE CHOICE TYPE)
2 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
Similar Questions
Knowledge Check
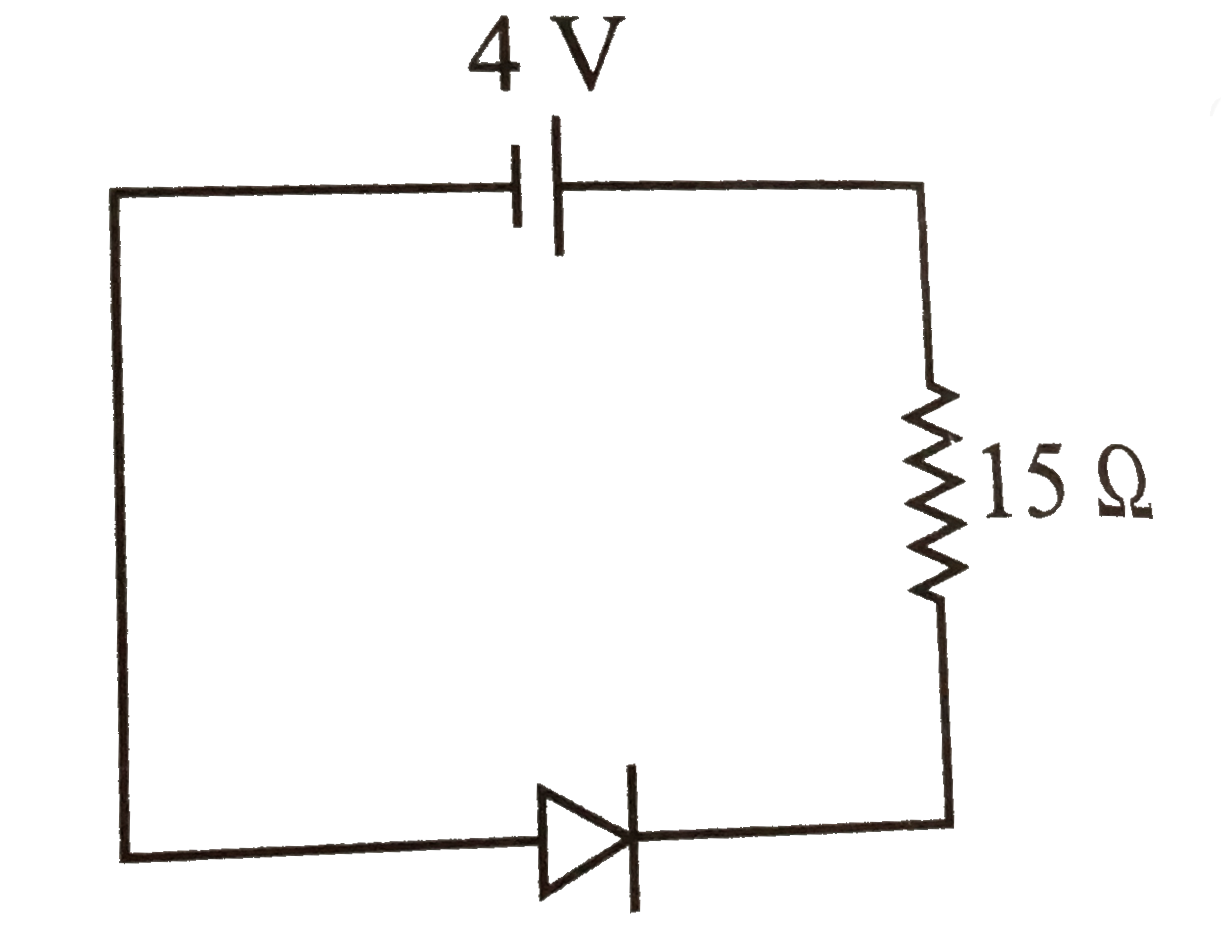
In the circuit shown if current for the diode is 20μA, the potential difference across the diode isA2 VB4.5VC4 VD2.5 V
If the potential difference across the ends of a conductor is doubled, the energy loss becomes-
View SolutionWhen a potential difference is applied across, the current passing through
View SolutionPotential difference across AB , i.e., VA−VB is

View SolutionThe displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
View SolutionThe displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
View SolutionGive, potential difference V = (8 + 0.5) V and current I = (2 + 0.2) A. The value of resistance R is
View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is
View Solution

