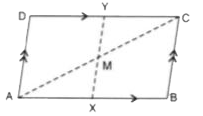
In the parallelogram ABCD ,M is mid-point of AC and X,Y are points on AB and DC respectively such that AX = CY.
Prove that :
(i) Triangle AXM is congruent to triangle
(ii) XMY is a straight line.
Step by step video solution for In the parallelogram ABCD ,M is mid-point of AC and X,Y are points on AB and DC respectively such that AX = CY. Prove that : (i) Triangle AXM is congruent to triangle (ii) XMY is a straight line. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - CONSTRUCTIONS OF POLYGONS
19 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - STATISTICS
2 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - MID-POINT THEOREM
12 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
Similar Questions
In the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:

O is mid-point of AP.
View SolutionA parallelogram ABCD has P the mid-point of DC and Q a point of AC such that CQ=14AC.PQ produced meets BC at R. Prove that:
PR=12DB.
View SolutionIn parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that:
(i) AX=YC.
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
View SolutionABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such that AB = BE and AD = DF. Prove that : ΔBEC≅ΔDCF.
View SolutionIn triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP=PMandCQ=QN. Prove that :
A is the mid-point of MN.
View SolutionIn triangle ABC, the sides AB and AC are equal. If P is a point on AB and Q is a point on AC such that AP = AQ, prove that :
(i) triangle APC and AQB are congruent.
(ii) triangle BPC and CQB are congruent.

View SolutionA parallelogram ABCD has P the mid-point of DC and Q a midpoint of AC such that CQ=14AC.PQ produced meets BC at R. Prove that:
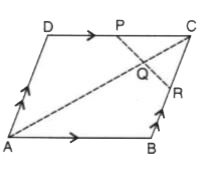
R is the mid-point of BC
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

BC= BE
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View Solution
