A line PQ is drawn parallel to the base BC of ΔABC which meets sides AB and AC at points P and Q respectively. If AP=13PB, find the value of :
Area of ΔABCArea of ΔAPQ
The correct Answer is:16:1
To find the ratio of the area of triangle ABC to the area of triangle APQ, we can follow these steps:
Step 1: Understand the Given Information
We have triangle ABC with a line PQ drawn parallel to the base BC. The line intersects sides AB and AC at points P and Q, respectively. We know that AP=13PB.
Step 2: Express AB in Terms of AP
Since AP=13PB, we can express PB in terms of AP:
- Let AP=x.
- Then PB=3x (because AP is one-third of PB).
- Therefore, the total length of AB is:
AB=AP+PB=x+3x=4x
Step 3: Use the Properties of Similar Triangles
Since line PQ is parallel to BC, triangles APQ and ABC are similar by the AA (Angle-Angle) criterion. The corresponding sides of similar triangles are in proportion.
Step 4: Set Up the Ratio of the Sides
The ratio of the sides of triangle ABC to triangle APQ can be expressed as:
ABAP=4xx=4
Step 5: Find the Ratio of the Areas
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore:
Area of △ABCArea of △APQ=(ABAP)2=42=16
Final Answer
Thus, the value of Area of △ABCArea of △APQ is:
16
---
We have triangle ABC with a line PQ drawn parallel to the base BC. The line intersects sides AB and AC at points P and Q, respectively. We know that AP=13PB.
Since AP=13PB, we can express PB in terms of AP:
- Let AP=x.
- Then PB=3x (because AP is one-third of PB).
- Therefore, the total length of AB is:
AB=AP+PB=x+3x=4x
Since line PQ is parallel to BC, triangles APQ and ABC are similar by the AA (Angle-Angle) criterion. The corresponding sides of similar triangles are in proportion.
The ratio of the sides of triangle ABC to triangle APQ can be expressed as:
ABAP=4xx=4
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore:
Area of △ABCArea of △APQ=(ABAP)2=42=16
Thus, the value of Area of △ABCArea of △APQ is:
16
Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(D)
18 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(B)
17 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
A line PQ is drawn parallel to the base BC of ΔABC which meets sides AB and AC at points P and Q respectively. If AP=13PB, find the value of :
Area of ΔAPQArea of trapeziumPBCQ
View SolutionA line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 90 cm, CA = 60 cm and AQ = 4.2 cm, find the length of AP.
View SolutionIn a ΔABC,PandQ are the mid-points of ABandAC respectively. If O is the circumcentre of the ΔABC, then the value of (Area of ΔABCArea of ΔOPQ)cotBcotC equal to
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionIn a ΔABC,D,EandF are the mid-point of sides BC, CA and AB respectively. If area of ΔABC=16cm2, find the area of trapezium FBCE
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
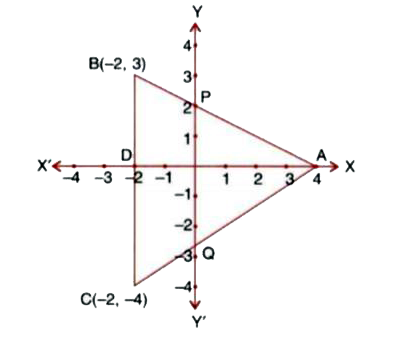
Find the length of AB and AC.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC

View SolutionIn ΔABC,∠B=90∘,AB=12cmandAC=15cm. D and E are points on AB and AC respectively such that ∠AED=90∘ and DE = 3 cm. Calculate the area of ΔABC and then the area of ΔADE.
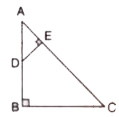
View SolutionA circle is touching the side BC of a △ABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter of △ABC).
View Solution
