ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQI/ BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP: AB.
The correct Answer is:(√2−1):√2
To solve the problem, we need to find the ratio BPAB given that line segment PQ is parallel to BC and divides triangle ABC into two parts of equal area.
1. Understanding the Given Information:
- Triangle ABC is given.
- Line segment PQ intersects AB at P and AC at Q.
- PQ∥BC and divides triangle ABC into two equal areas.
2. Using the Area Property:
- Since PQ∥BC, triangles APQ and ABC are similar by the Basic Proportionality Theorem (also known as Thales' theorem).
- The area of triangle APQ is equal to half the area of triangle ABC.
3. Setting Up the Area Ratio:
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- Let AP=x and PB=y. Therefore, AB=x+y.
- The area of triangle APQ can be expressed as:
Area of APQ=12Area of ABC
- Since the areas are in the ratio APQABC=(APAB)2, we have:
12Area of ABCArea of ABC=(APAB)2
- This simplifies to:
12=(xx+y)2
4. Solving for the Ratio:
- Taking the square root of both sides gives:
1√2=xx+y
- Rearranging this gives:
x=1√2(x+y)
- Expanding and rearranging:
x=x√2+y√2
x−x√2=y√2
- Factoring out x:
x(1−1√2)=y√2
- Thus, we have:
yx=√2(1−1√2)
5. Finding BPAB:
- Since BP=y and AB=x+y, we can express the ratio:
BPAB=yx+y
- Substituting y=√2x−x:
BPAB=√2x−xx+(√2x−x)=(√2−1)x√2x
- This simplifies to:
BPAB=√2−1√2
Final Answer:
The value of the ratio BPAB is √2−1√2.
- Triangle ABC is given.
- Line segment PQ intersects AB at P and AC at Q.
- PQ∥BC and divides triangle ABC into two equal areas.
- Since PQ∥BC, triangles APQ and ABC are similar by the Basic Proportionality Theorem (also known as Thales' theorem).
- The area of triangle APQ is equal to half the area of triangle ABC.
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- Let AP=x and PB=y. Therefore, AB=x+y.
- The area of triangle APQ can be expressed as:
Area of APQ=12Area of ABC
- Since the areas are in the ratio APQABC=(APAB)2, we have:
12Area of ABCArea of ABC=(APAB)2
- This simplifies to:
12=(xx+y)2
- Taking the square root of both sides gives:
1√2=xx+y
- Rearranging this gives:
x=1√2(x+y)
- Expanding and rearranging:
x=x√2+y√2
x−x√2=y√2
- Factoring out x:
x(1−1√2)=y√2
- Thus, we have:
yx=√2(1−1√2)
- Since BP=y and AB=x+y, we can express the ratio:
BPAB=yx+y
- Substituting y=√2x−x:
BPAB=√2x−xx+(√2x−x)=(√2−1)x√2x
- This simplifies to:
BPAB=√2−1√2
The value of the ratio BPAB is √2−1√2.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(D)18videos
SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)
- BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)61videos
SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)
- BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(B)17videos
SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)
- BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)10videos
SIMILARITY
- BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )18videos
SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)
Similar Questions
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
View SolutionABC is a triangle right angled at C. If AB=25cmandAC=7cm, find BC.
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionD is a point in side BC of triangle ABC. If AD>AC, show that AB>AC.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.View SolutionM and N divide the side AB of a triangle ABC into three equal parts . Through M and N, lines are drawn parallel to BC and intersecting AC at points P and Q respectively. Prove that P and Q divide AC into three equal parts.
View SolutionGiven a triangle ABC with AB=2 and AC=1. Internal bisector of ∠BAC intersects BC at D. If AD = BD and Δ is the area of triangle ABC, then find the value of 12Δ2.
View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.
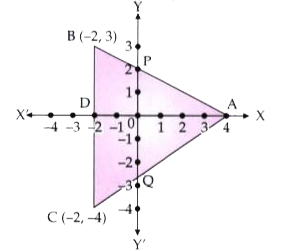
(iv) Find the equation of the line AC.View Solution

