A line PQ is drawn parallel to the base BC of ΔABC which meets sides AB and AC at points P and Q respectively. If AP=13PB, find the value of :
Area of ΔAPQArea of trapeziumPBCQ
The correct Answer is:1:15
To solve the problem, we need to find the ratio of the area of triangle APQ to the area of trapezium PBCQ. Given that AP = 1/3 PB, we can follow these steps:
Step 1: Understand the relationship between AP and PB
Given that AP=13PB, we can express PB in terms of AP:
PB=3⋅AP
Step 2: Express the lengths in terms of a single variable
Let AP=x. Then:
PB=3x
The total length of AB can be expressed as:
AB=AP+PB=x+3x=4x
Step 3: Use the properties of similar triangles
Since line PQ is parallel to the base BC of triangle ABC, triangles APQ and ABC are similar by the AA (Angle-Angle) similarity criterion. Therefore, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
Step 4: Find the ratio of the sides
The ratio of the sides of triangle APQ to triangle ABC is:
APAB=x4x=14
Step 5: Find the ratio of the areas
Using the property of similar triangles, the ratio of the areas is:
Area of △APQArea of △ABC=(APAB)2=(14)2=116
Step 6: Express the area of trapezium PBCQ
The area of trapezium PBCQ can be found by subtracting the area of triangle APQ from the area of triangle ABC:
Area of trapezium PBCQ=Area of △ABC−Area of △APQ
Let the area of triangle ABC be A. Then:
Area of △APQ=116A
Thus, the area of trapezium PBCQ is:
Area of trapezium PBCQ=A−116A=1616A−116A=1516A
Step 7: Find the ratio of the areas
Now we can find the required ratio:
Area of △APQArea of trapezium PBCQ=116A1516A=115
Final Answer
The value of Area of △APQArea of trapezium PBCQ is:
115
Given that AP=13PB, we can express PB in terms of AP:
PB=3⋅AP
Let AP=x. Then:
PB=3x
The total length of AB can be expressed as:
AB=AP+PB=x+3x=4x
Since line PQ is parallel to the base BC of triangle ABC, triangles APQ and ABC are similar by the AA (Angle-Angle) similarity criterion. Therefore, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
The ratio of the sides of triangle APQ to triangle ABC is:
APAB=x4x=14
Using the property of similar triangles, the ratio of the areas is:
Area of △APQArea of △ABC=(APAB)2=(14)2=116
The area of trapezium PBCQ can be found by subtracting the area of triangle APQ from the area of triangle ABC:
Area of trapezium PBCQ=Area of △ABC−Area of △APQ
Area of △APQ=116A
Thus, the area of trapezium PBCQ is:
Area of trapezium PBCQ=A−116A=1616A−116A=1516A
Now we can find the required ratio:
Area of △APQArea of trapezium PBCQ=116A1516A=115
The value of Area of △APQArea of trapezium PBCQ is:
115
Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(D)
18 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(B)
17 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
A line PQ is drawn parallel to the base BC of ΔABC which meets sides AB and AC at points P and Q respectively. If AP=13PB, find the value of :
Area of ΔABCArea of ΔAPQ
View SolutionA line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 90 cm, CA = 60 cm and AQ = 4.2 cm, find the length of AP.
View SolutionIn a ΔABC,PandQ are the mid-points of ABandAC respectively. If O is the circumcentre of the ΔABC, then the value of (Area of ΔABCArea of ΔOPQ)cotBcotC equal to
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionIn a ΔABC,D,EandF are the mid-point of sides BC, CA and AB respectively. If area of ΔABC=16cm2, find the area of trapezium FBCE
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
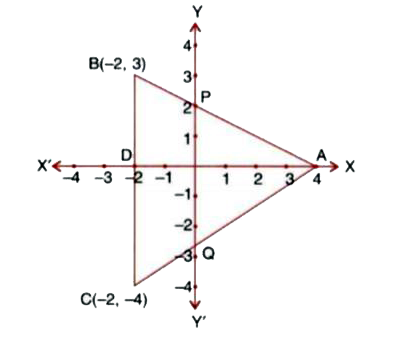
Find the length of AB and AC.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.
View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.
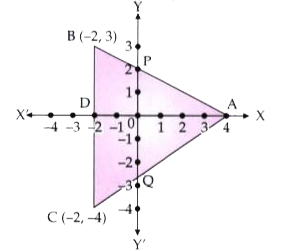
(iv) Find the equation of the line AC.
View SolutionIn triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and Glines are drawn parallel to AB which meet side BC at points M and N respectively.
Prove that : BM = MN = NC.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
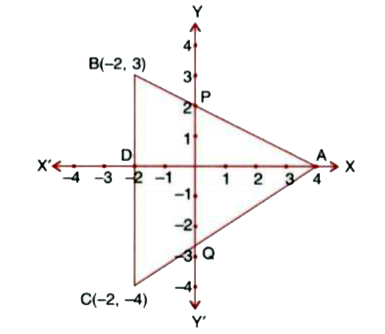
Write the co-ordinates of A.
View Solution
