In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
To solve the problem, we need to find the ratio AXAB given that the line segment XY is parallel to side AC of triangle ABC and divides the triangle into two parts of equal areas.
1. Understanding the Given Information:
- We have triangle ABC.
- Line segment XY is parallel to side AC.
- The area of triangle XYB is equal to the area of triangle XYC.
2. Setting Up the Area Relationship:
- Since XY divides triangle ABC into two equal areas, we can express this as:
Area of XYB+Area of XYC=Area of ABC
- Let AXYB=AXYC=A. Thus, we have:
A+A=AABC⟹AABC=2A
3. Using Similar Triangles:
- Since XY is parallel to AC, triangles AXY and ABC are similar by the Angle-Angle (AA) similarity criterion.
- Therefore, we can write the ratio of their areas:
AABCAXYB=(ABXY)2
4. Substituting the Areas:
- We know AABC=2A and AXYB=A:
2AA=(ABXY)2⟹2=(ABXY)2
5. Taking the Square Root:
- Taking the square root of both sides gives:
ABXY=√2
6. Finding the Ratio AXAB:
- Let AX=x and XB=AB−x.
- From the similarity of triangles, we have:
AXAB=XYAC
- Since XY is parallel to AC, we can express this as:
AXAB=1√2
7. Final Result:
- Therefore, the ratio AXAB is:
AXAB=√2−1
- We have triangle ABC.
- Line segment XY is parallel to side AC.
- The area of triangle XYB is equal to the area of triangle XYC.
- Since XY divides triangle ABC into two equal areas, we can express this as:
Area of XYB+Area of XYC=Area of ABC
- Let AXYB=AXYC=A. Thus, we have:
A+A=AABC⟹AABC=2A
- Since XY is parallel to AC, triangles AXY and ABC are similar by the Angle-Angle (AA) similarity criterion.
- Therefore, we can write the ratio of their areas:
AABCAXYB=(ABXY)2
- We know AABC=2A and AXYB=A:
2AA=(ABXY)2⟹2=(ABXY)2
- Taking the square root of both sides gives:
ABXY=√2
- Let AX=x and XB=AB−x.
- From the similarity of triangles, we have:
AXAB=XYAC
- Since XY is parallel to AC, we can express this as:
AXAB=1√2
- Therefore, the ratio AXAB is:
AXAB=√2−1
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.4
9 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.1
3 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.2
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.3
9 Videos
Similar Questions
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQI/ BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP: AB.
View SolutionIn ABC , PQ is a line segment intersecting AB at P and AC at Q such that PQBC and PQ divides ABC into two parts equal in area. Find BPAB .
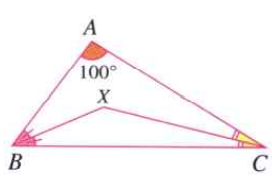
View SolutionIn ΔABC,∠=100∘. Line segment BX divides ∠B into two equal parts and CX divides ∠C into two equal parts. Find ∠BXC.
View SolutionX and Y are points on the sides AB and BC respectively of △ABC such that XY||AC and XY divides △ABC into two parts in area , find AXAB
View SolutionIn Figure, if line segment AB is parallel to the line segment CD, what is the value of y? (a)12 (b) 15 (c) 18 (d) 20
View SolutionD and E are points on the sides AB and AC respectively of a ABC such that DEBC and divides ABC into two parts, equal in area, find BDAB .
View SolutionIn each of the figures [4.222 (i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segments are marked. Find the value of x in each of the following: (FIGURE)
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: O is also the mid-point of BD
View SolutionThe line segment joining the mid-points of any two sides of a triangle in parallel to the third side and equal to half of it.
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: AOB≅ DOC.
View Solution
