In the figure given below O is the centre of the circumcircle of triangle XYZ.
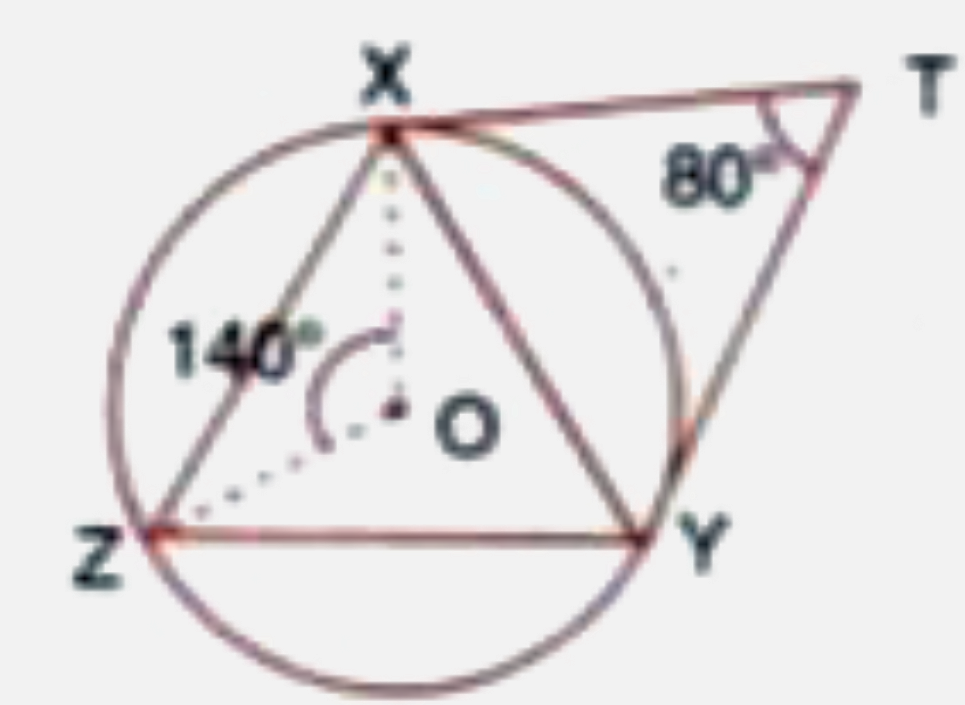
Tangents at X and Y intersect at point T. Given ∠XTY=80∘ and ∠XOZ=140∘, calculate the value of ∠ZXY.
The correct Answer is:60∘
Step by step video & image solution for In the figure given below O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given /_XTY=80^(@) and /_XOZ=140^(@), calculate the value of /_ZXY. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
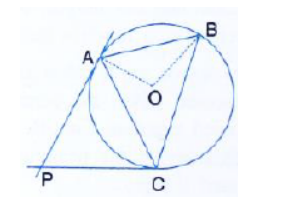
In the given figure, O is the centre of the circumcircle of △ABC. Tangents at A and C intersect at P. Given angle AOB=140∘ and angle APC=80∘ find the angle BAC.
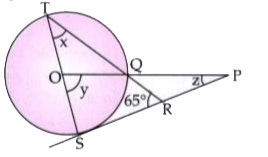
View SolutionIn the figure given below, O is the centre of the cirlce and SP is a tangent. If ∠SRT=65∘, find the value of x, y and z.
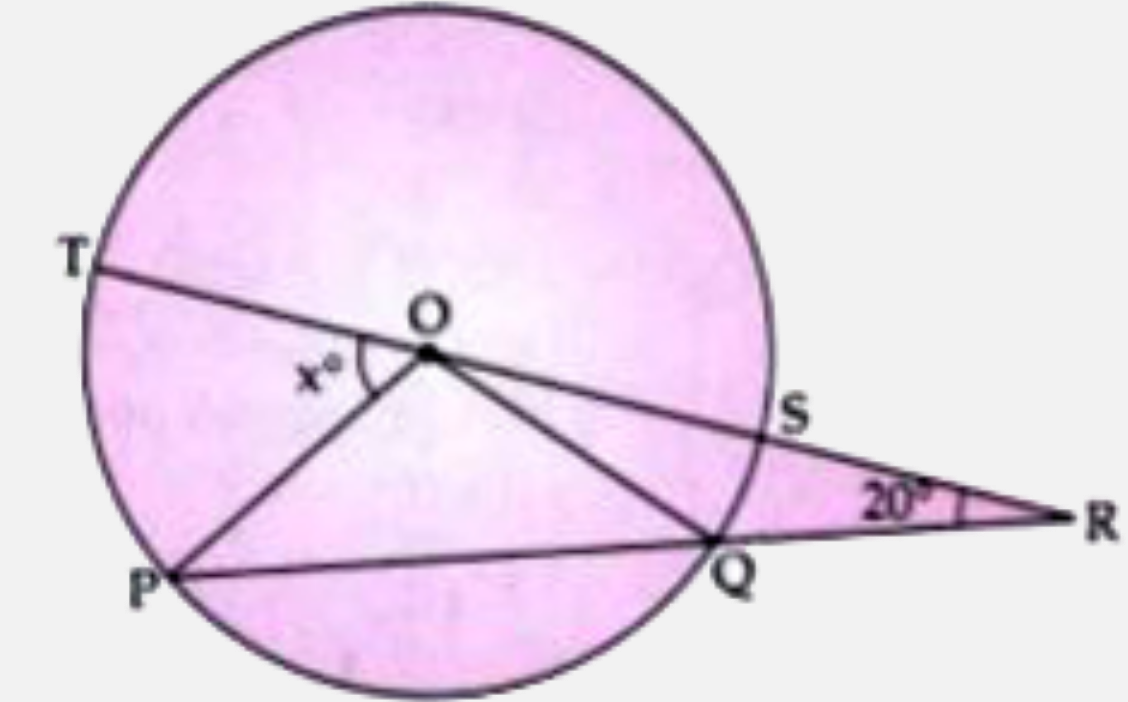
View SolutionIn the figure given below 'O' is the centre of the circle. If QR = OP and ∠ORP=20∘. Find the value of 'x'
View SolutionIn the given figure O is the centre of the circle. Tangents at A and B meets at C.
If ∠ACO=30∘, find
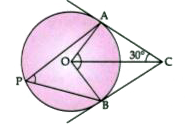
∠BCO
View SolutionIn the given figure O is the centre of the circle. Tangents at A and B meets at C.
If ∠ACO=30∘, find
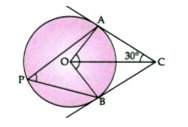
∠AOB
View SolutionIn the given figure O is the centre of the circle. Tangents at A and B meets at C.
If ∠ACO=30∘, find

∠APB
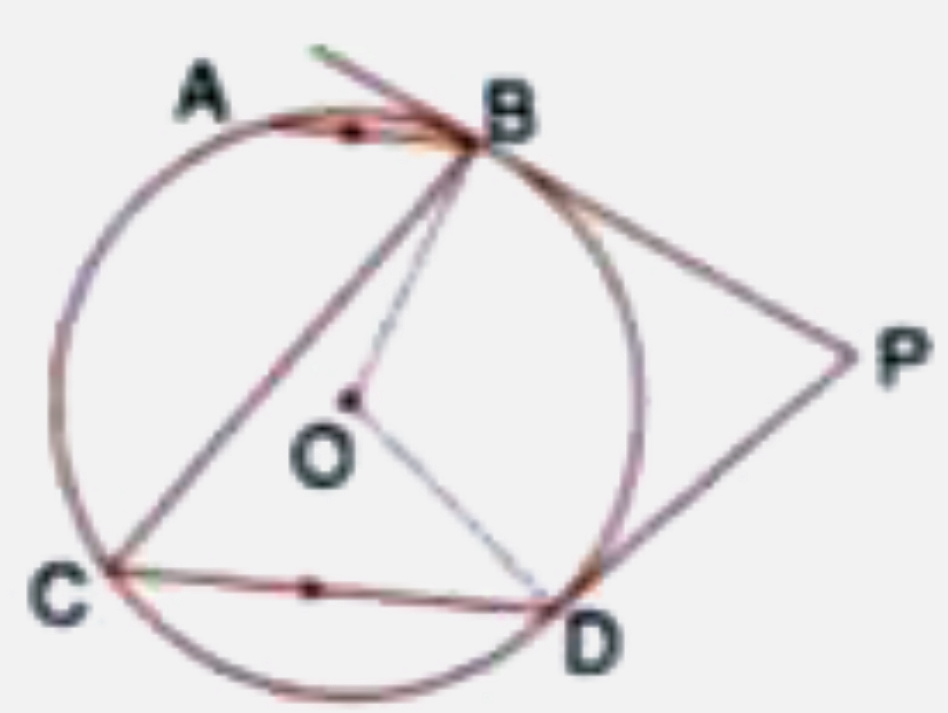
View SolutionIn the given figure O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC=55∘, find :
(i) ∠BOD (ii) ∠BPD
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:
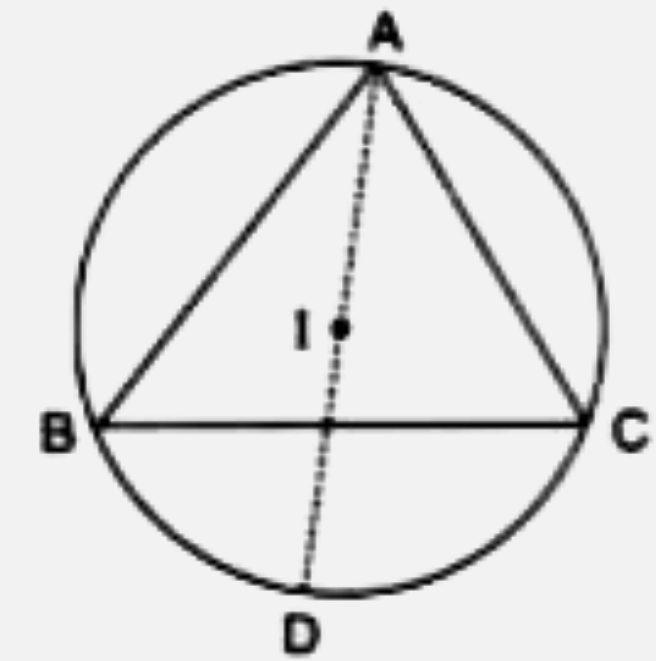
∠DCI
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:

∠BCD
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:

∠CBD
View Solution
