In the given figure PAT is tangent to the circle with centre O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segment show that
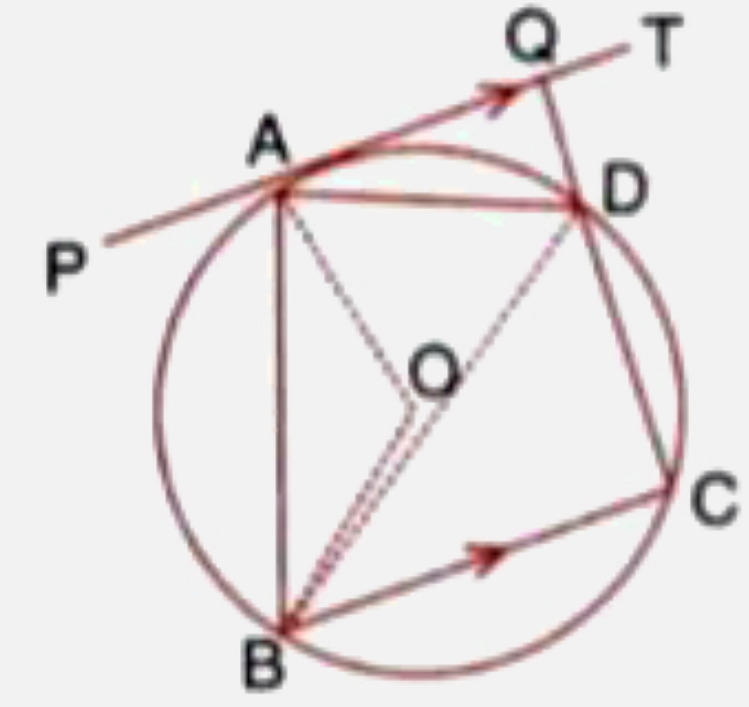
(i) ∠BAP=∠ADQ
(ii) ∠AOB=2∠ADQ
(iii) ∠ADQ=∠ADB
Step by step video & image solution for In the given figure PAT is tangent to the circle with centre O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segment show that (i) /_BAP=/_ADQ (ii) /_AOB=2/_ADQ (iii) /_ADQ=/_ADB by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
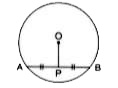
The given figure shows a circle with centre O. P is mid-point of chord AB.
Show that OP is perpendicular to AB.
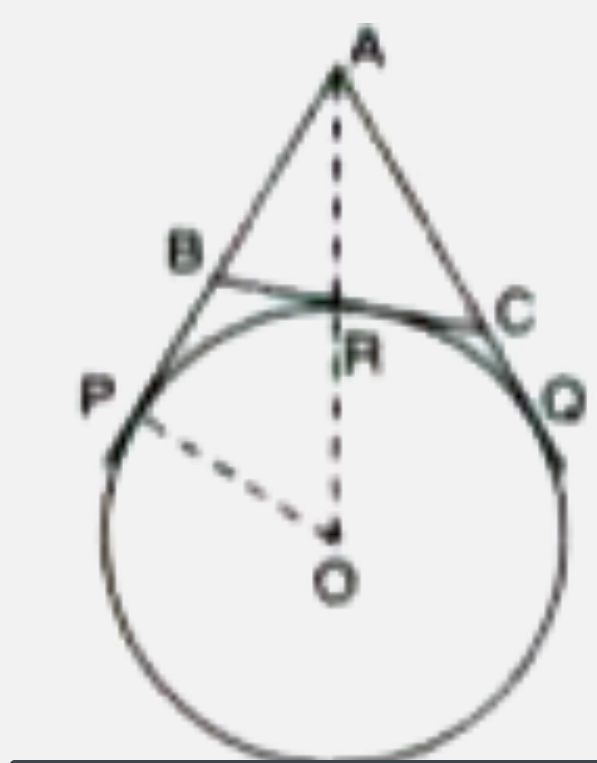
View SolutionIn the given figure AP and AQ are tangents to the circle with centre O. BC is tangent at point R on it.
If OA=17 cm and radius of the circle =8cm, find the perimeter of the triangle ABC.
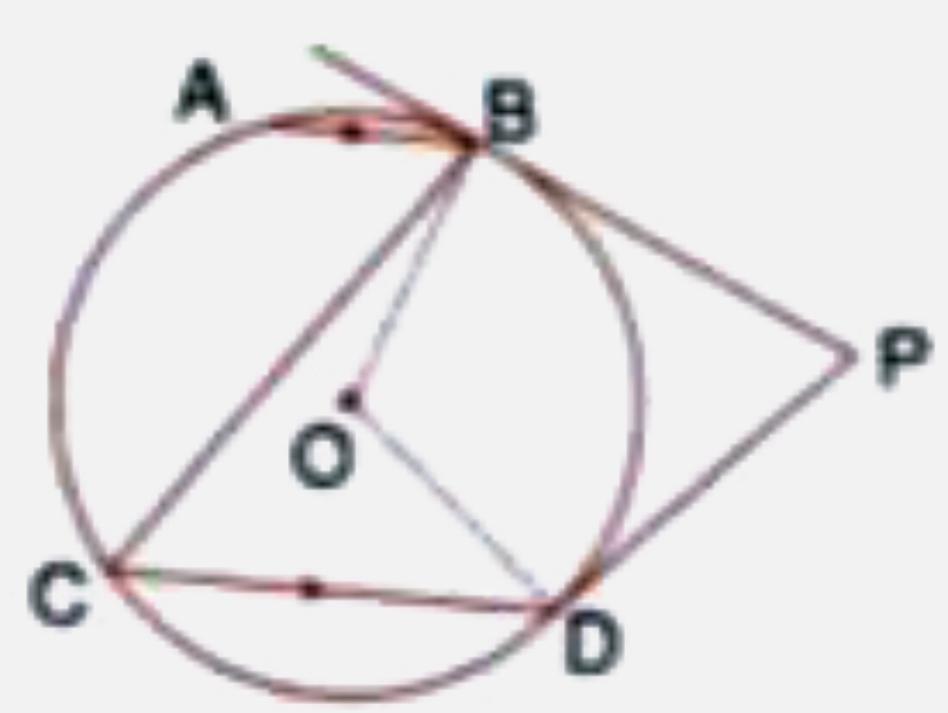
View SolutionIn the given figure O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC=55∘, find :
(i) ∠BOD (ii) ∠BPD
View SolutionIn the figure AB is the chord of a circle with centre O and DOC is a line segment such that BC=DO. If ∠C=20∘, find angle AOD.
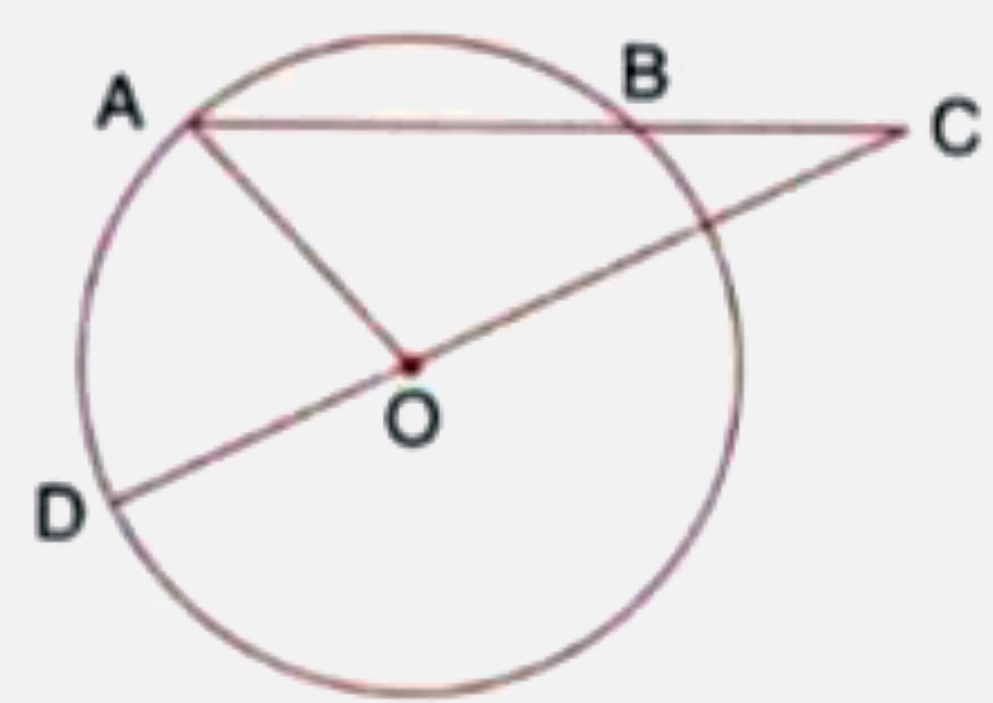
View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre O from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionIn the following figure PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB=30∘ and ∠CBD=60∘. Calculate :

(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB
View SolutionIn the given figure , AD is a diameter O is the centre of the circle AD is parallel to BC and ∠CBD=32∘
(i) ∠OBD
(ii )∠AOB
(iii) ∠BED

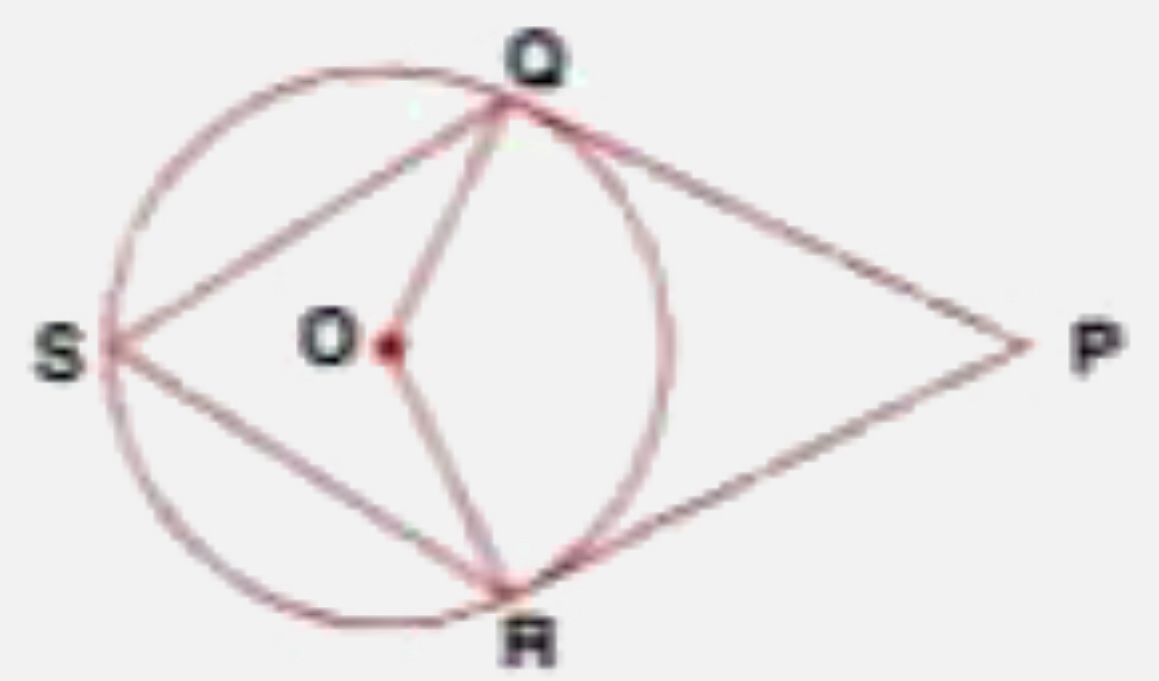
View SolutionIn the following figure PQ and PR are tangents to the circle with the centre O. If ∠QPR=60∘ calculate
(i)∠QOR
(ii) ∠OQR
(iii) ∠QSR
View SolutionIn the given figure O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO=30∘ find
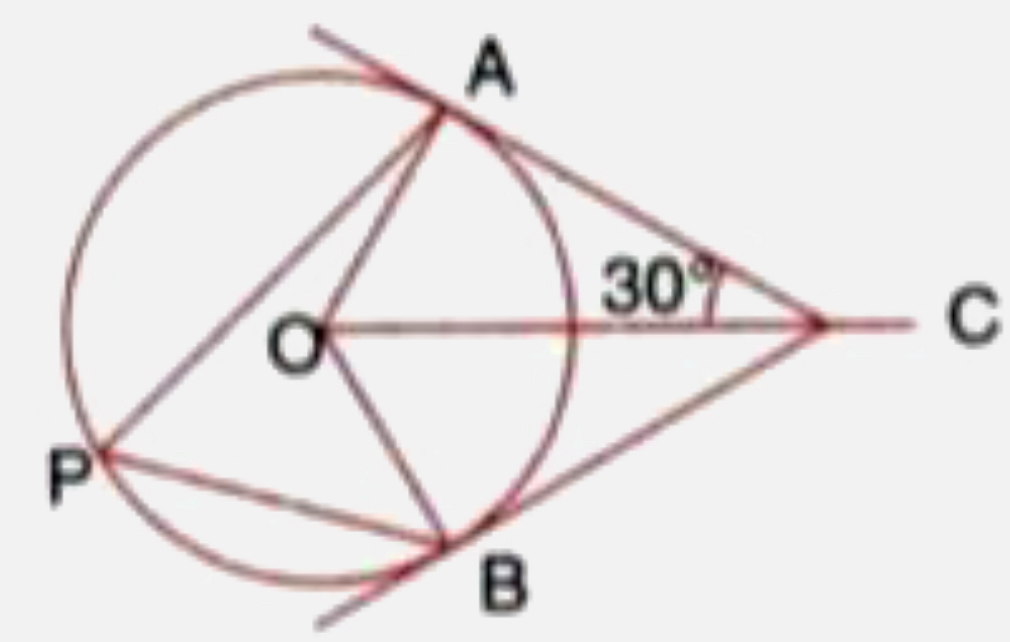
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB
View Solution
