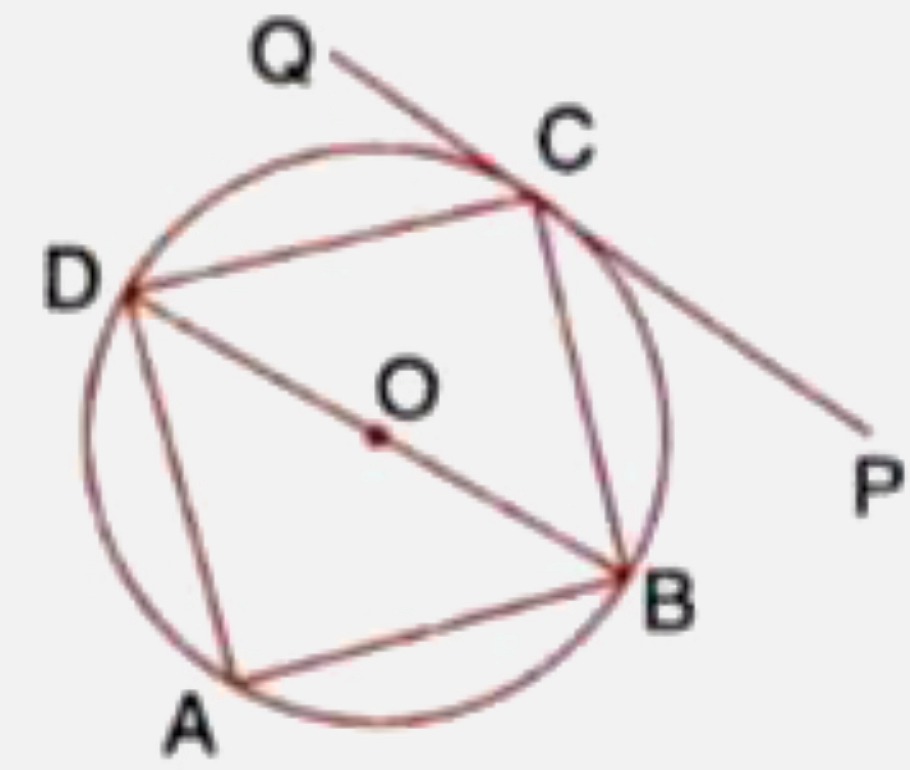
In the given figure QAP is the tangent at point A and PBD is a straight line.
If ∠ACB=36∘ and ∠APB=42∘, find
(i) ∠BAP (ii) ∠ABD
(iii) ∠QAD (iv) ∠BCD
The correct Answer is:(i) 36∘ (ii) 78∘ (iii) 78∘ (iv) 114∘
Step by step video & image solution for In the given figure QAP is the tangent at point A and PBD is a straight line. If /_ACB=36^(@) and /_APB=42^(@), find (i) /_BAP (ii) /_ABD (iii) /_QAD (iv) /_BCD by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)18videos
TANGENTS AND INTERSECTING CHORDS
- BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C12videos
SPECIMEN QUESTION PAPER (MATHEMATICS)
- BOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS22videos
TRIGONOMETRICAL IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure AOB is a straight line Find
(i) ∠AOC
A35∘B40∘C75∘D25∘
In the given figure O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO=30∘ find
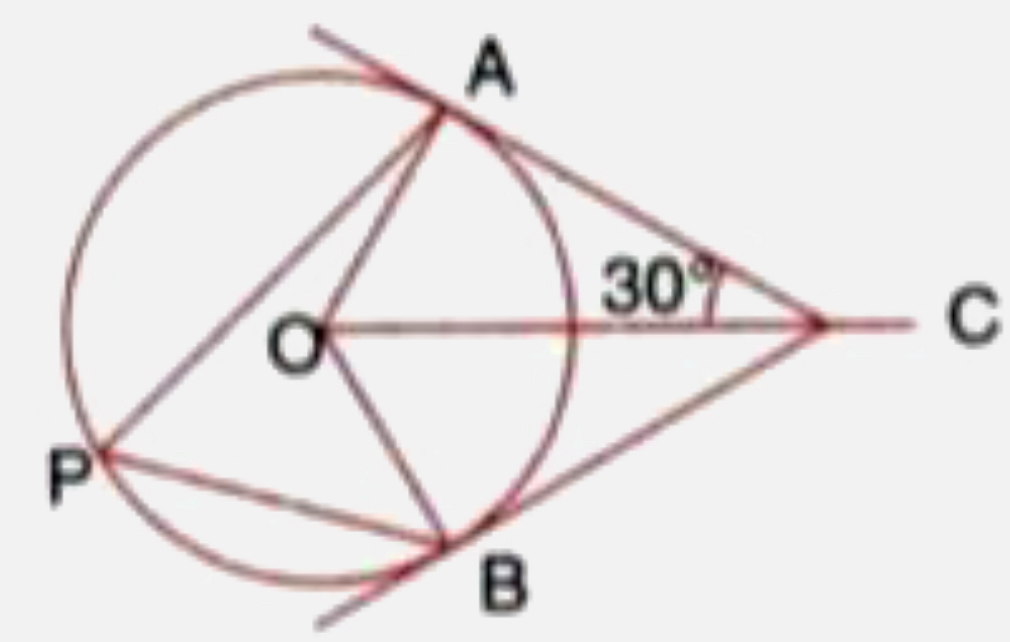
(i) ∠BCO
(ii) ∠AOB
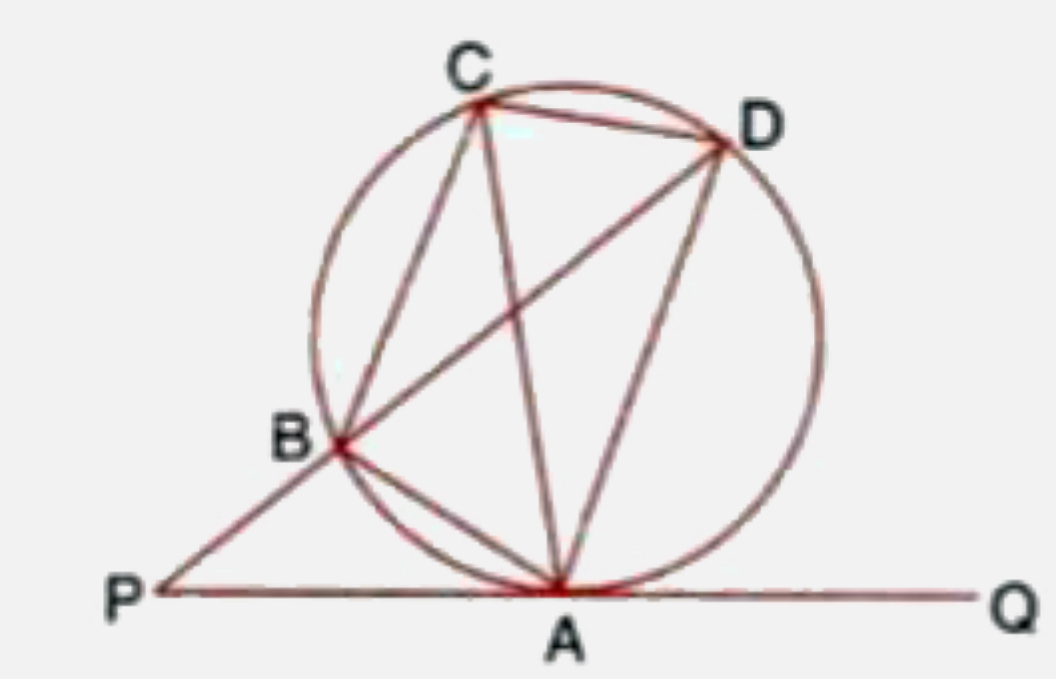
(iii) ∠APBView SolutionIn the given figure AB is the diameter. The tangent at C meets AB produced at Q.
If ∠CAB=34∘ find
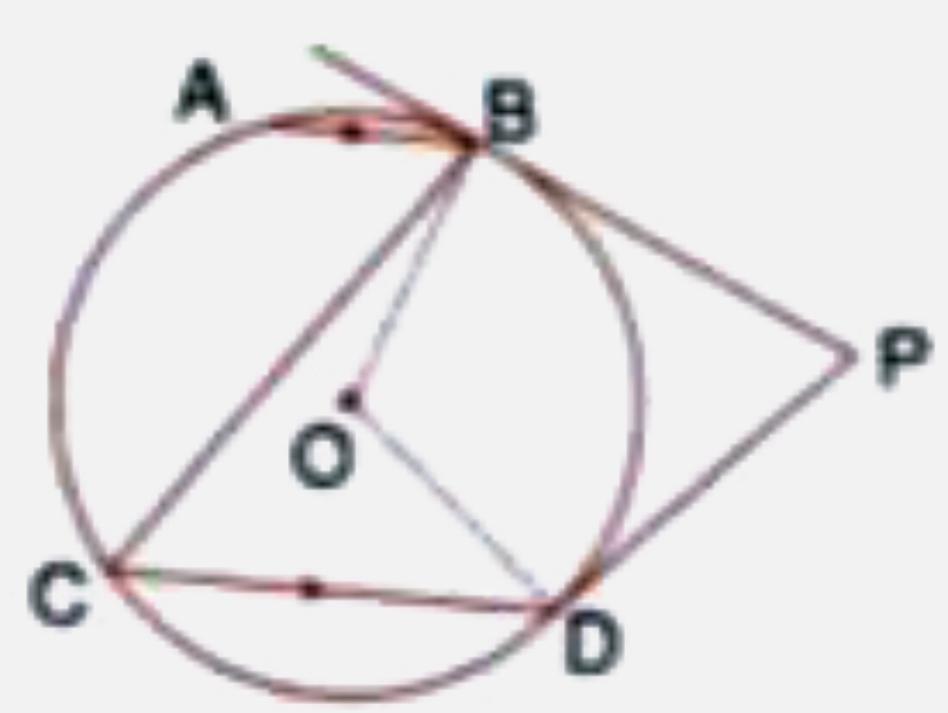
(i) ∠CBA (ii)∠CQBView SolutionIn the given figure O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC=55∘, find :
(i) ∠BOD (ii) ∠BPD
View SolutionIn the figure given below, O is the centre of the circle and Ab is a diameter.
If AC = BC and ∠AOC=72∘. Find:
(i) ∠ABC
(ii) ∠BAD
(iii) ∠ABD
View SolutionIn the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (-4, 2) and AP : PB = 1 : 2. Find the co-ordinates A and B .
View SolutionIn the given figure PAT is tangent to the circle with centre O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segment show that
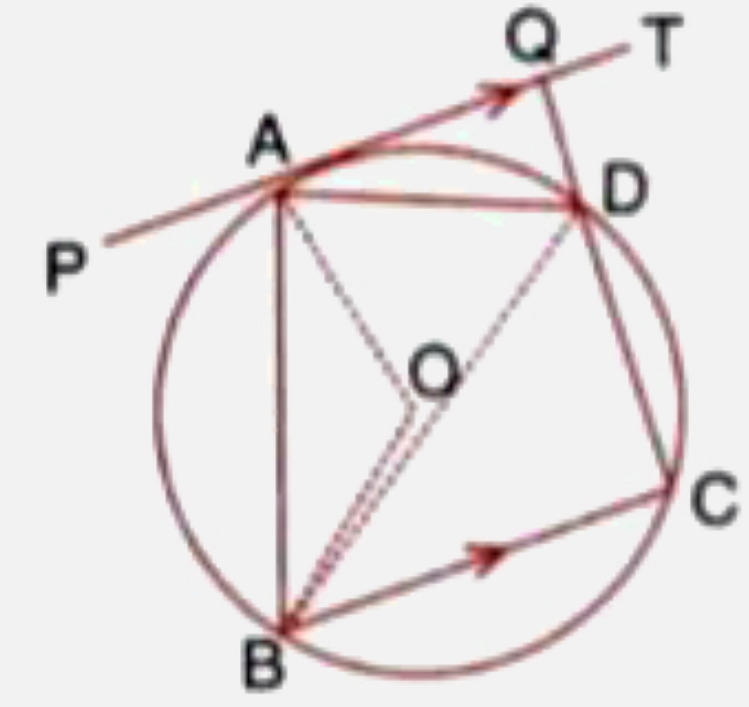
(i) ∠BAP=∠ADQ
(ii) ∠AOB=2∠ADQ
(iii) ∠ADQ=∠ADBView SolutionIn the adjoining figure, POQ is a straight line. Find the m and n when
(i) m−n=60∘
(ii) m:n=7.5
View Solution