At distance 'r' from a point charge, the ratio UV2 (where 'U' is energy density and 'V' is potential) is best respresented by :


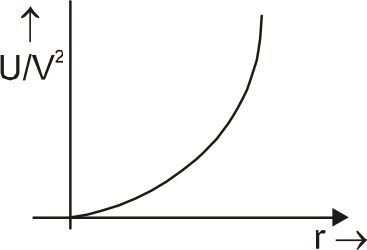
To solve the problem, we need to find the ratio UV2 where U is the energy density and V is the electric potential at a distance r from a point charge Q.
1. Understand the Definitions:
- The electric potential V at a distance r from a point charge Q is given by:
V=kQr
where k is Coulomb's constant.
2. Calculate the Electric Field E:
- The electric field E at a distance r from a point charge Q is given by:
E=kQr2
3. Calculate the Energy Density U:
- The energy density U in an electric field is given by:
U=12ϵ0E2
- Substituting the expression for E:
U=12ϵ0(kQr2)2
- Simplifying this gives:
U=12ϵ0k2Q2r4
4. Calculate V2:
- Now, we find V2:
V2=(kQr)2=k2Q2r2
5. Find the Ratio UV2:
- Now we can find the ratio:
UV2=12ϵ0k2Q2r4k2Q2r2
- Simplifying this ratio:
UV2=12ϵ0k2Q2r4⋅r2k2Q2=12ϵ01r2
6. Conclusion:
- The final expression for the ratio UV2 is:
UV2=12ϵ0r2
- This shows that UV2 is inversely proportional to r2.
Answer:
The ratio UV2 is best represented by a hyperbolic relationship as r varies, confirming that it is inversely proportional to r2.
- The electric potential V at a distance r from a point charge Q is given by:
V=kQr
where k is Coulomb's constant.
- The electric field E at a distance r from a point charge Q is given by:
E=kQr2
- The energy density U in an electric field is given by:
U=12ϵ0E2
- Substituting the expression for E:
U=12ϵ0(kQr2)2
- Simplifying this gives:
U=12ϵ0k2Q2r4
- Now, we find V2:
V2=(kQr)2=k2Q2r2
- Now we can find the ratio:
UV2=12ϵ0k2Q2r4k2Q2r2
- Simplifying this ratio:
UV2=12ϵ0k2Q2r4⋅r2k2Q2=12ϵ01r2
- The final expression for the ratio UV2 is:
UV2=12ϵ0r2
- This shows that UV2 is inversely proportional to r2.
The ratio UV2 is best represented by a hyperbolic relationship as r varies, confirming that it is inversely proportional to r2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges are placed at (n−1) corners. At the centre, the intensity is E and the potential is V. The ratio V/E has magnitude
ArnBr(n−1)C(n−1)/rDr(n−1)/n
At a certain distance from a point charge, the field intensity is 500V/m and the potential is −3000V. The distance to the charge and the magnitude of the charge respectively are
View SolutionAt a certain distance from a point charge, the field intensity is 500V/m and the potentil is −3000V. The distance to the charge and the magnitude of the charge respectively are
View SolutionA point moves in a straight line under the retardation av2, where 'a' is a positive constant and v is speed. If the initial speed is u, the distance covered in 't' seconds is :
View SolutionIn a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges are placed at (n−1) corners. At the centre, the intensity is E and the potential is V. The ratio V/E has magnitude
View SolutionPlot a graph comparing the variation of potential ‘V’ and electric field ‘E’ due to a point charge ‘Q’ as a function of distance r from point charge
(ii) Find the ratio of the potential differences that must be applied across the parallel and the series combination of two identical capacitors so that the energy stored, in the two cases, becomes the same.
View SolutionThe quantity 2UfkT represents (where U= internal energy of gas)
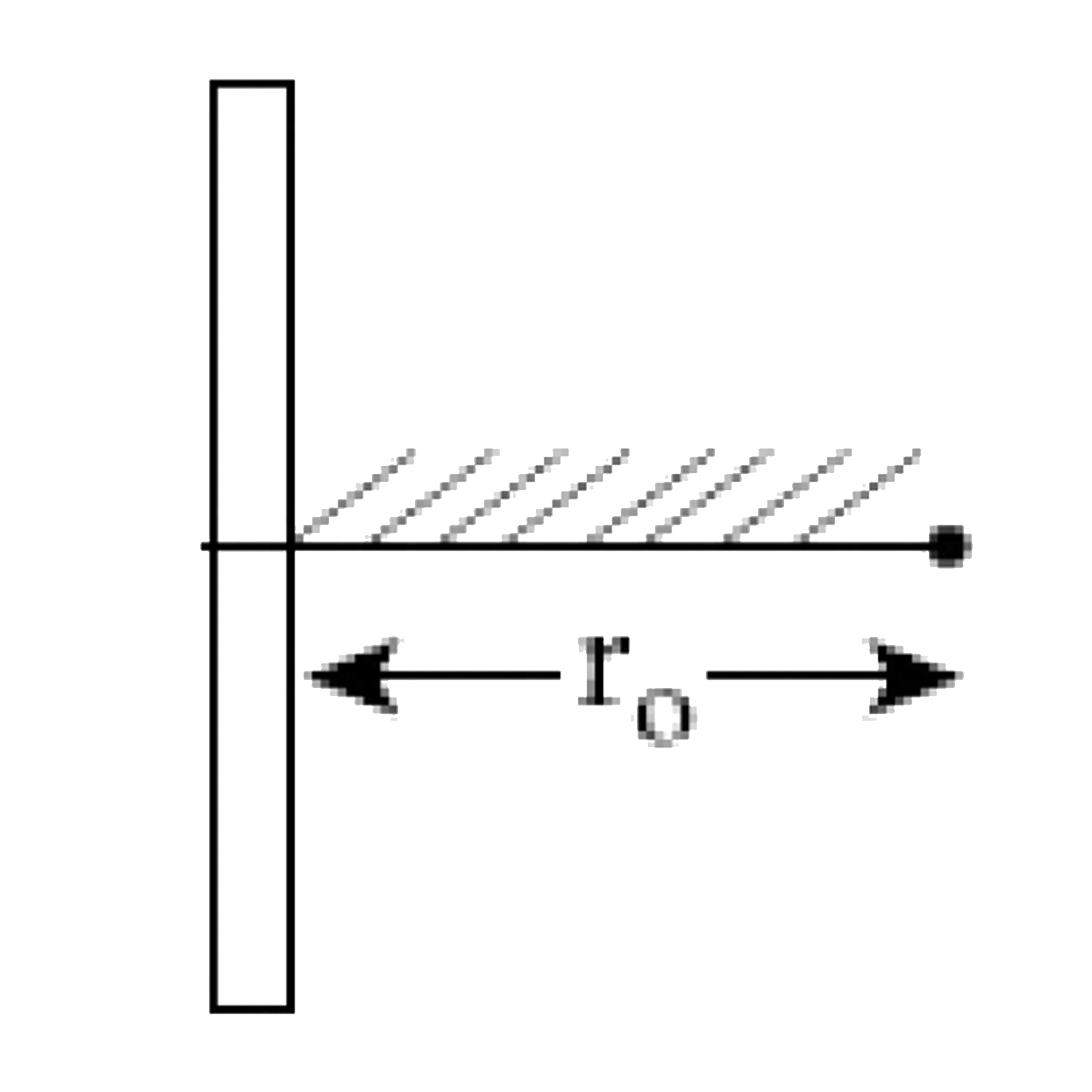
View SolutionA positive charge is released from rest at a distance r0 from a positive line charge with uniform density . The speed (v) of the point charge , as a function of instantaneous distance r from line charge, is proportional to:
View Solution
