A hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.
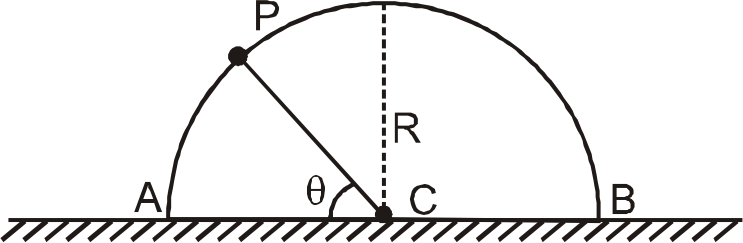
When the insect reaches point ‘P’ of the hemisphere the displacement of hemisphere w.r.t. ground is :
Zero
(mM+m)v2Rcosθ horizontally towards left
(MM+m)v2Rsinθ horizontally towards right
(mM+m)v2Rcosθ horizontally towards right
Momentum of system in horizontal will remain conserved, so
MV=m(vsinθ−V)
⇒V=mvM+msinθ
dVdt=mvM+mcosθ(dθdt)
(dVdt)=(mM+m)v2Rcosθ
Topper's Solved these Questions
Similar Questions
A hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.
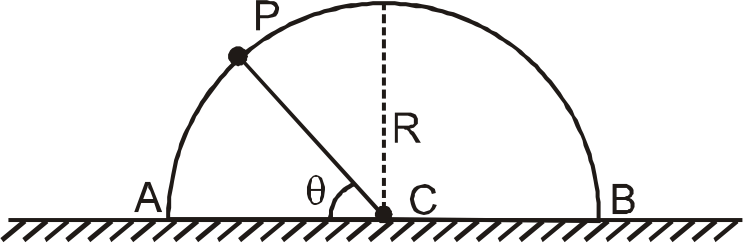
When insect at point ‘P’ on the bowl the displacement of centre of mass of the system (bowl + insect) is :
View SolutionA strip of wood of mass M and length l is placed on a smooth horizontal surface. An insect of mass m starts at one end of the strip and walks to the other end in time t, moving with a constant speed. The speed of the insect as seen from the ground is
View SolutionA hemispherical bowl is made of steel 0.5 cm thick. The inside radius of the bowl is 4cm.
View SolutionA hemispherical bowl has a radius of 3.5 cm. What would be the volume of water it would contain?
View SolutionA hemispherical bowl has inner diameter 11.2cm. Find the volume of milk it can hold.
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View SolutionA small solid sphere of mass m and radius r starting from rest from the rim of a fixed hemispherical bowl of radius R(>>r) rolls inside it without sliding. The normal reaction exerted by the sphere on the hemisphere when it reaches the bottom of hemisphere is

View SolutionWhen a magnet is dipped in a bowl of iron filings, the poles of the magnet attract
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View Solution
