A rigid bent light rod of total length 2l can slide on fixed wire frame with the help of frictionless sliders. There is thin liquid film (surface tension T) between bent rod and wire frame. In equilibrium the elongation in spring is given by (4Tlα5K). then find the value of α.
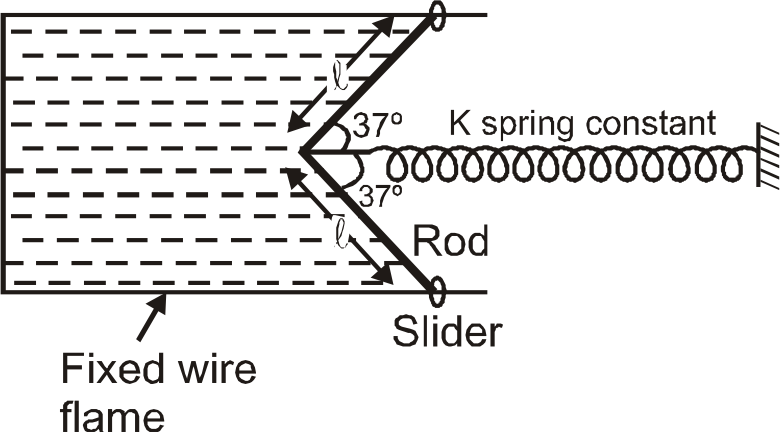
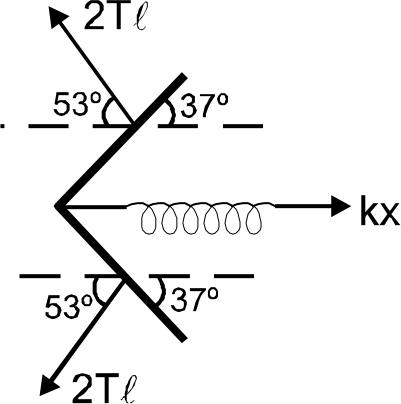
2(2Tl)cos53∘=Kx
4Tl35K=x
Topper's Solved these Questions
Similar Questions
The surface tension of a thin liquid film formed between a U shaped wire and a light slider of length 30 cm supporing a weight of 1.5×10−2N is
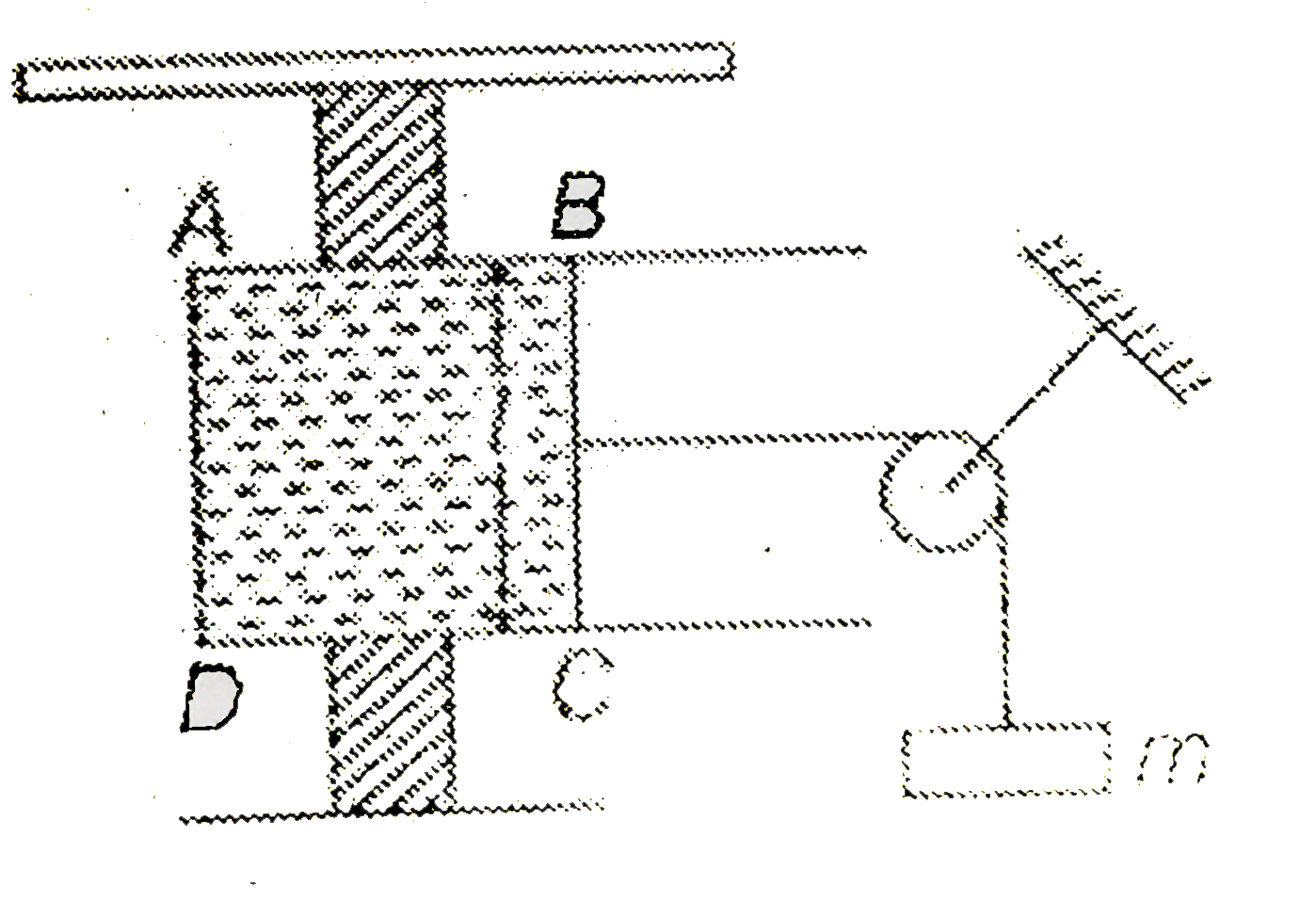
View SolutionA wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
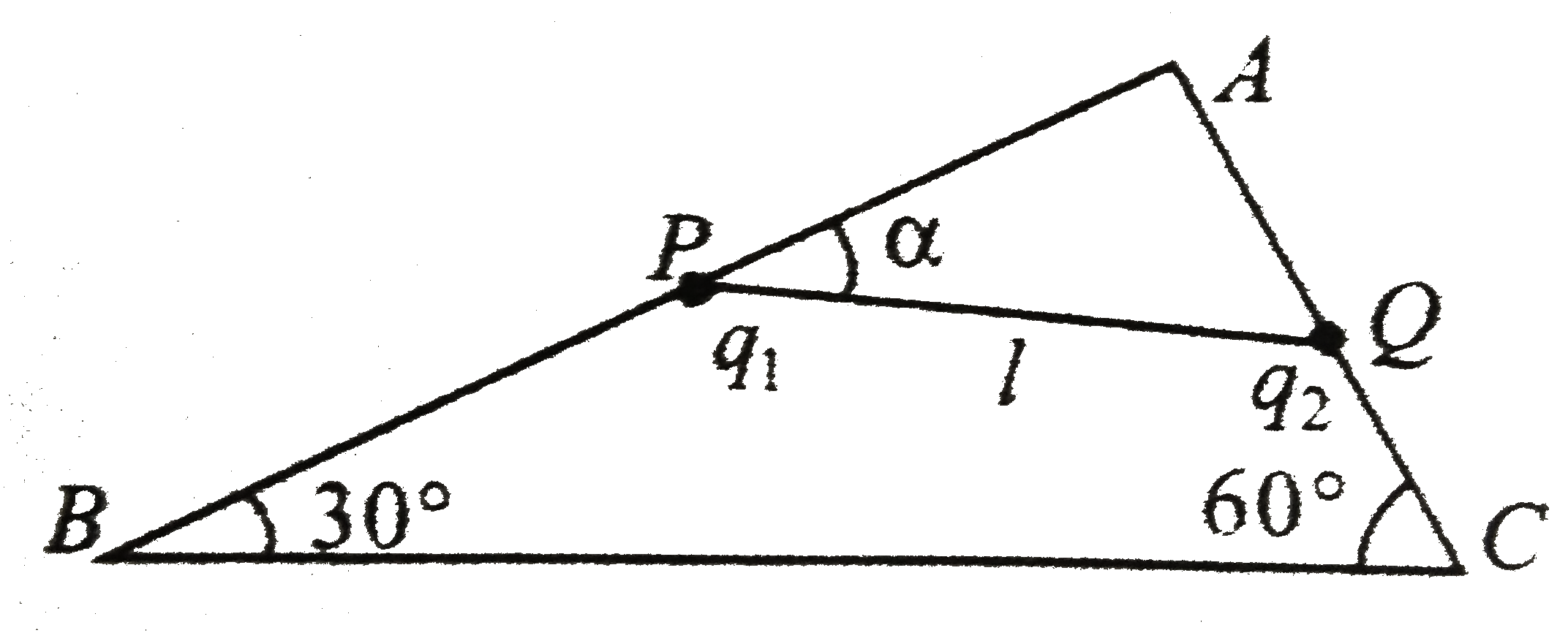
View SolutionA rigid insulated wire frame in the form of a right-angled triangle ABC is set in a vertical plane as shown in fig. two beads of equal masses m each and carrying charges q1 and q2 are connected by a cord of length l and can slide without friction on the wires.
Cinsidering the case when the beads are stationary, determine
(i) the angel α
(ii) the tension in the cord, and
(iii) The normal recation on teh beads.
If the cord is now cut, what are the value of the charges for which the beads continue to remain stationary?
View Solution
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View Solution
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View SolutionA light wire AB of length 10 cm can slide on a vertical frame as shown in figure. There is a film of soap solution trapped between the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soat solution =25 dyne cm−1. Take g=10ms−2

View SolutionA thin and light thread of sufficient length L is attached to a wire frame. The frame (along with the thread) is dipped into soap solution. When the frame is taken out of the solution, the thread takes the form of a semicircle with a soap film extending between the frame and the thread as shown in the figure (a). Now the thread is deformed into two semicircles by applying a force of F at the middle of the thread, as a result the film gets strectched as shown in the figure. (b). Calculate the surface tension of the soap solution.

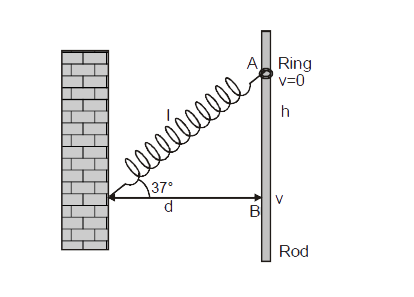
View SolutionOne end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
View SolutionOn end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal. as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. (sin37∘=35).

View SolutionA block A of mass M kept on a rough horizontal surface is connected to a dielectric slab of mass M/6 and dielectric constant k by means of a light and inextensible string passing over a fixed pulley as shown in the figure. The dielectric can completely fill the space between the parallel plate capacitor of plate area l×l and separation between the plates d kept in vertical position. Initially switch S is open and length of the dielectric inside the capacitor is b. The coefficient of friction between the block A and the surface is μ=1/4. Igonore any other friction. (Given Mgdε0l(k−1)=24.)
Find the minimum value of the emf =V of the battery so that after closing the switch the block A will move.

View Solution
