A sphere of density falls vertically downward through a fluid of density . At a certain instant its velocity is u. The terminal velocity of the sphere is . Assuming that stokes’s law for viscous drag is applicable, the instantaneous acceleration of the sphere is found to be . here is in an integer. find .
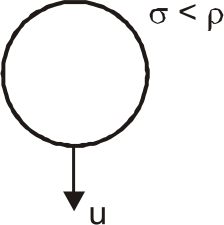
Topper's Solved these Questions
Similar Questions
A solid ball of density ρ1 and radius r falls vertically through a liquid of density ρ2. Assume that the viscous force acting on the ball is F=krv, where k is a constant and v its velocity. What is the terminal velocity of the ball ?
View SolutionA sperical object of mass 1kg and radius 1 m is falling vertically downward inside a viscous liquid in a gravity free space. At a certain instant the velocity of the sphere is 2 m/s. if the coefficient of viscosity of the liquid is 118πN−S/m2 then velocity of ball will become 0.5 m/s after a tie
View SolutionA sphere of mass m and radius r is projected in a gravity free space with speed v. If the coefficient of viscosity of the medium in which it moves is 1/6π Pa s, the distance travelled by the body before it stops is :
View SolutionAn iron ball of radius 0.3 cm falls through a column of oil of density 0.94gcm−3 .It is found to attain a terminal velocity of 0.5cms−1. Determine the viscosity of the oil. Given that the density of iron is 7.8gcm−3
View SolutionA particle performs linear S.H.M. At a particular instant, velocity of the particle is u and acceleration is α while at another instant, velocity is v and acceleration β (0<α<β). The distance between the two position is
View SolutionA sphere is dropped into a viscous liquid of viscosity η from some height if the density of material and liquid are ρ and σ respectively (ρ>σ) then which of the following is/are incorrect.
(a). The acceleration of the sphere just after entering the liquid is g(ρ−σρ)
(b). Time taken to attain terminal speed t∝ρ0
(C)AT TERMINAL SPEED VISCOUS FORCE IS MAXIMUM (d). At terminal speed, the net force acting on the sphere is zero.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
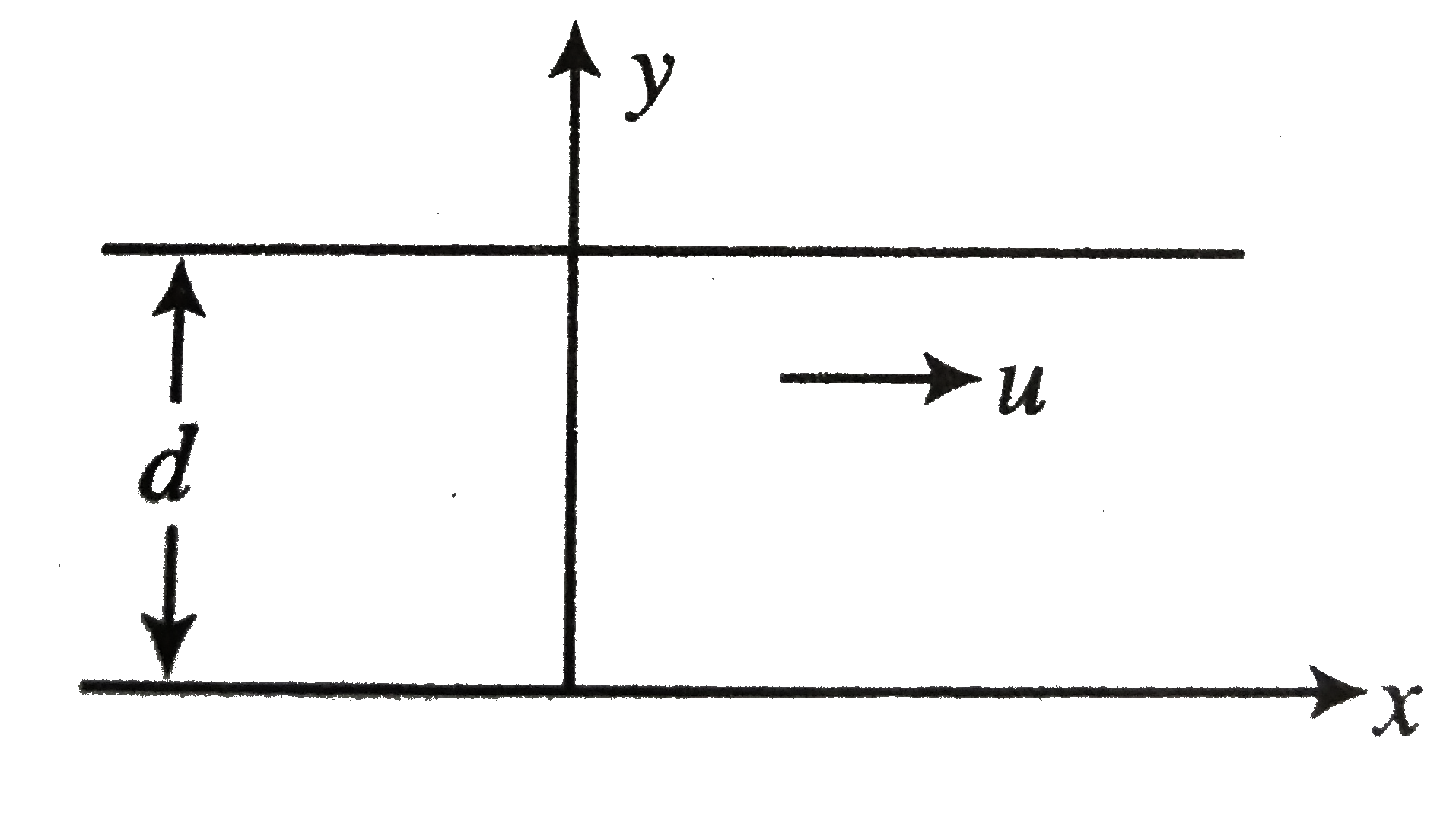
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. Find time taken by him to across the river.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
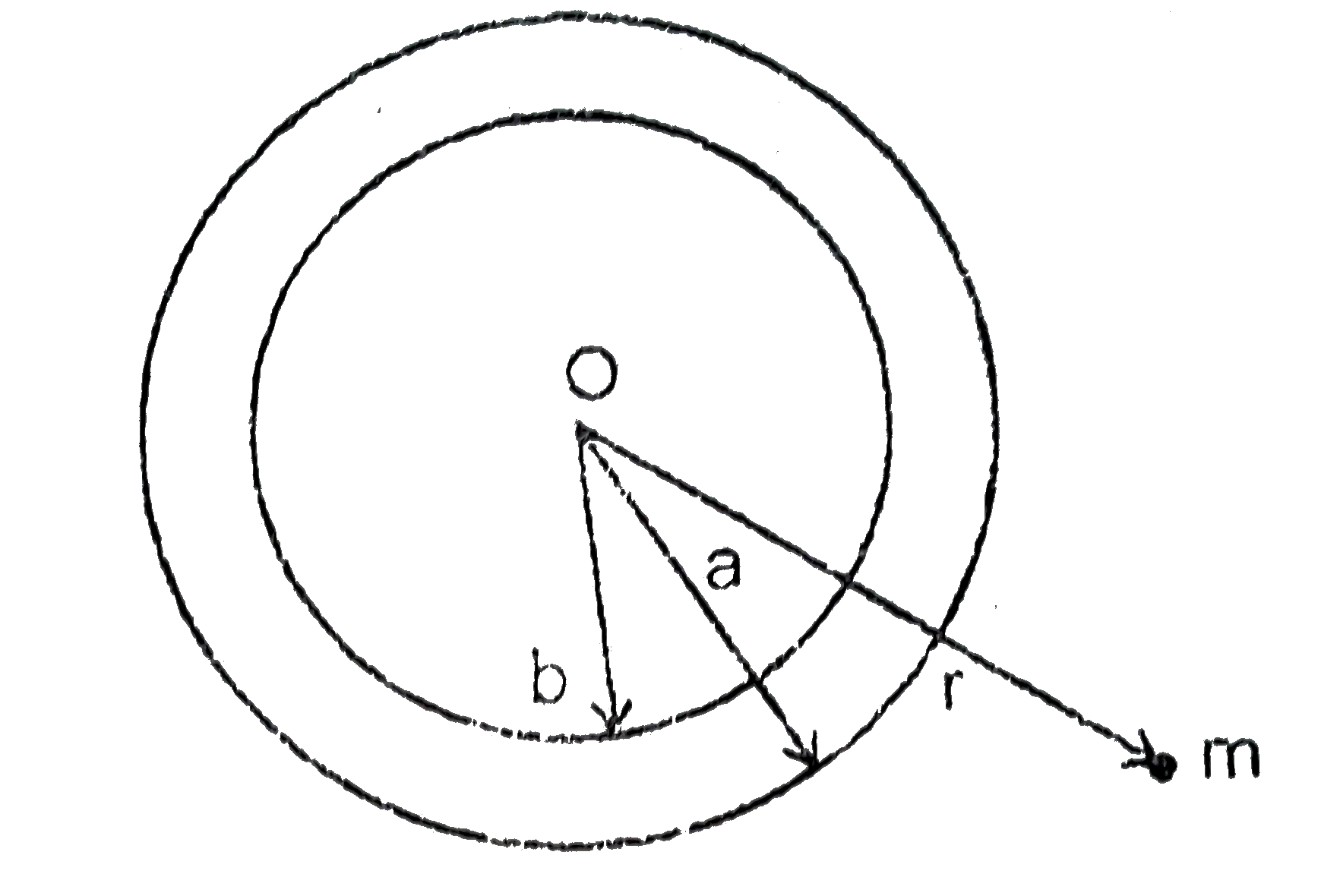
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionA sphere of density ρ and radius a has a concentric of radius b as shown in the
(a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range 0≤r≤∞
(b) Sketch the corresponding curve for the potential energy u (r) of the system
 ,View Solution
,View Solution

