There is a step of height h on an incline plane. The step prevents a ball of radius R from rolling down. If the inclination (θ) to the incline is increased gradualluy, at some value of θ the ball will just manage to climb the step then value of θ is.
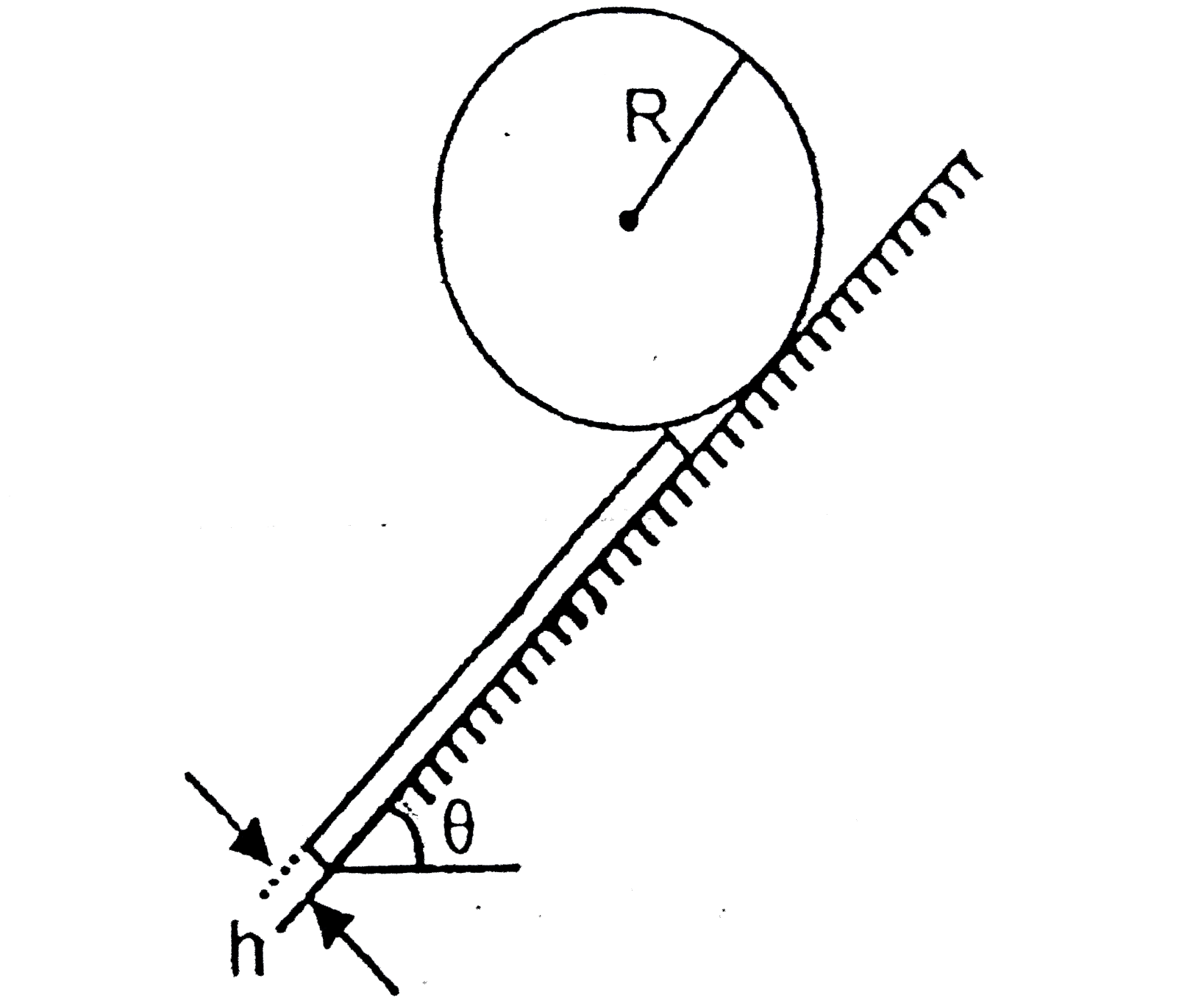
cosθ=RR+h
cosθ=R−hR
cosθ=R−2hR
sinθ=R−hR
The correct Answer is:B
(a) The ball begin to climb the step if the line of action of its weight (Mg) passes to the left to point A. This will cause an unbalanced torque about A.
In critical case (see figure) cosθ=R−hR
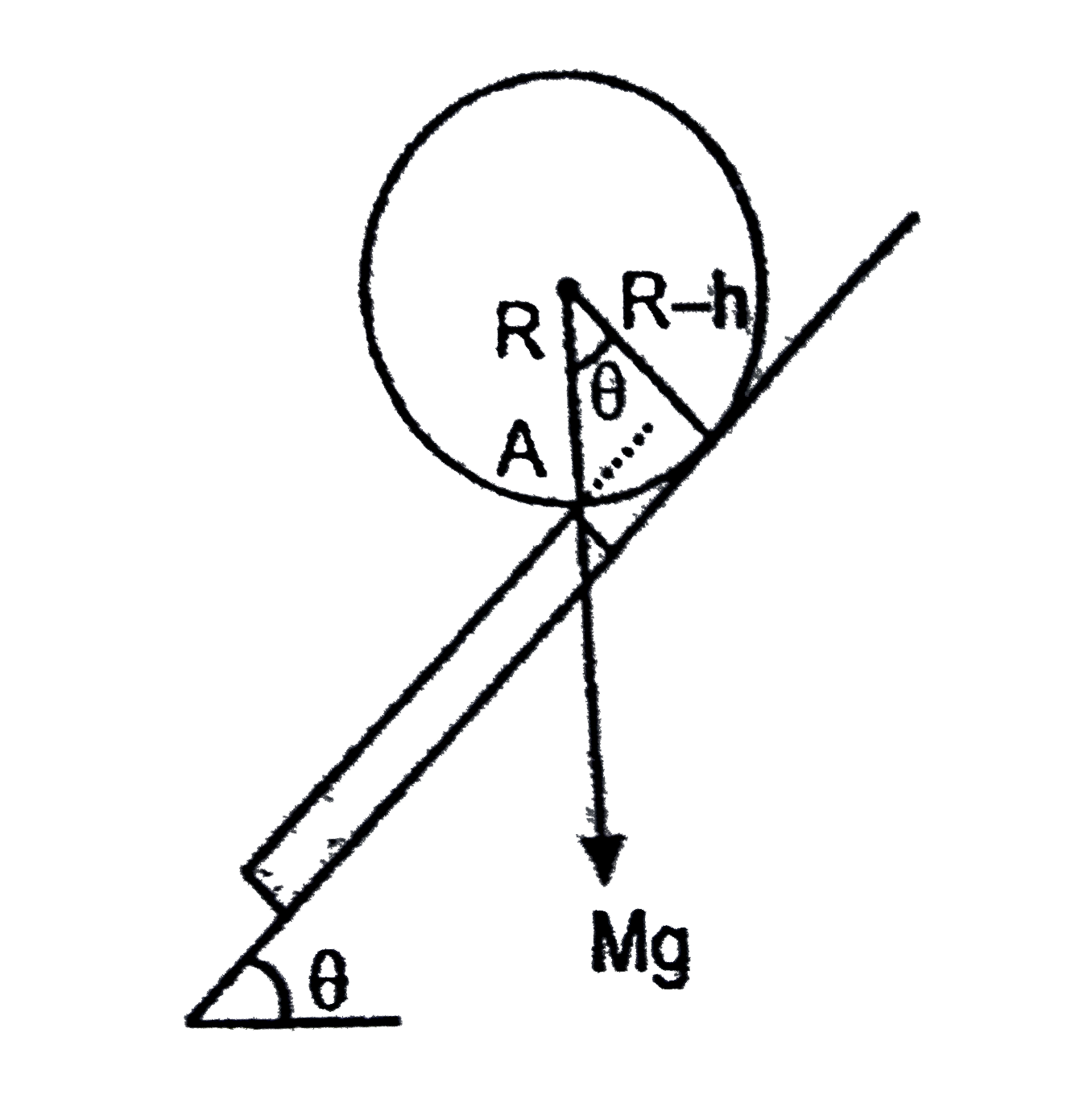
(b) In the position shown, the COM of the ball is vertically above point A at a distance R. As the ball climbs, its centre of mass will lover from this position. (Otherwise why will the ball come down?) In the position shown the centre of mass is at highest position.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A spherical shell of radius R is rolling down an incline of inclination θ without slipping. Find minimum value of coefficient of friction.

View SolutionA disc of radius R is rolling down an inclined plane whose angle of inclination is θ Its acceleration would be
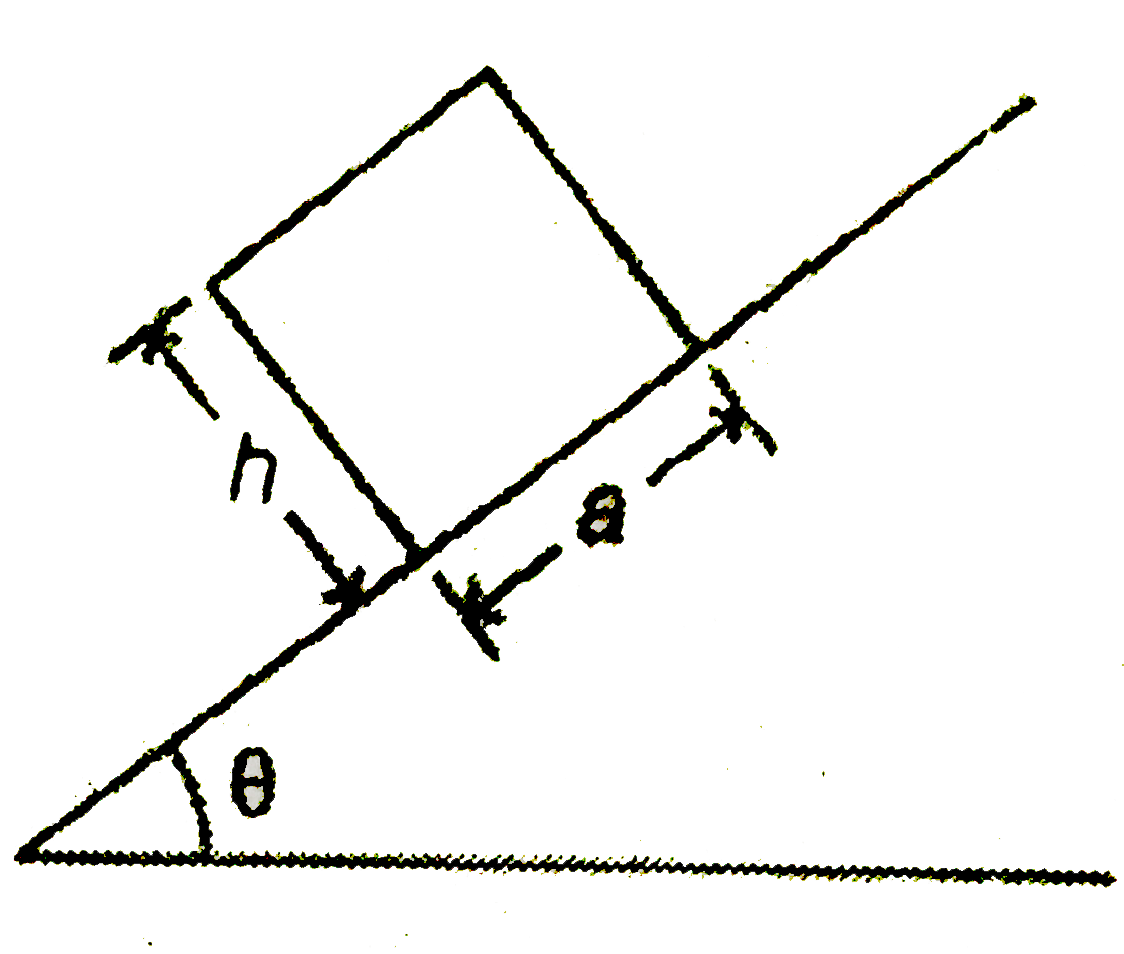
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
View SolutionA sphere is rolling down a plane of inclination θ to the horizontal. The acceleration of its centre down the plane is
View SolutionA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
View SolutionA sphere starts rolling down can incline of inclination theta. Find the speed of its centre when it has covered a distance l.
View SolutionThe velocity of a sphere rolling down an inclined plane of height h at an inclination θ with the horizontal, will be :
View SolutionA solid cylinder of radius r rolls down an inclined plane of height h and inclination θ. Calculate its speed at the bottom of the plane using energy method. Also calculate the time taken to reach of the bottom.
View SolutionA cube of side a is placed on an inclined plane of inclination θ. What is the maximum value of θ for which the cube will not topple?

View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View Solution
