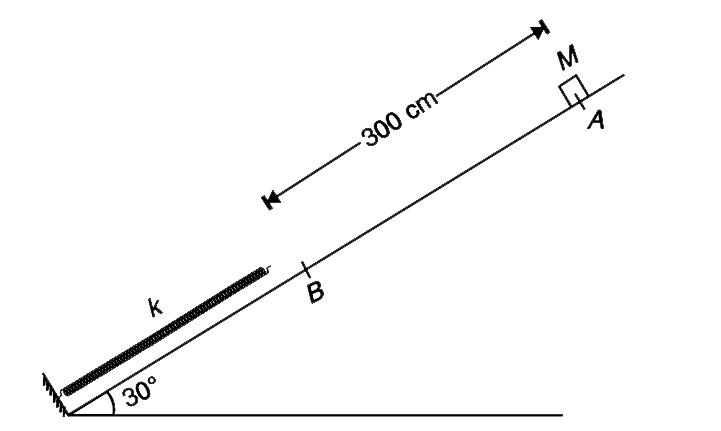
A block of mass M = 40 kg is released on a smooth incline from point A. After travelling through a length of 30 cm it strikes an ideal spring of force constant K=1000N/m . It compresses the spring and then gets pushed back. How much time after its release, the block will be back to point A?
4sec.
2.5sec.
1.54sec.
3.26sec.
The correct Answer is:C
Time to travel from A to B(t1) is given by -
x=ut+12at2,[∴a=gsinθ=5m/s2]
0.3=12×5×t21⇒t1=0.35s
Speed of the block when it hits the spring is given by -
V2=02+2ax=2×5×0.3
V=√3m/s
The motion of the block in contact with the spring can be regarded as a part of SHM. In equilibrium, compression in the spring is given by
kx0=mgsinθ
x0=40×10×121000=0.2m
Let the block compress the spring by a length x1.
Energy conservation gives -
12kx21=12MV2+Mgx1sinθ
12×1000.x21=12×40×(√3)2×(40×10×12)x1
5x21−2x1−0.6m
Solving x1=0.5m
Hence, amplitude of SHM is A=x1−x0=0.4m
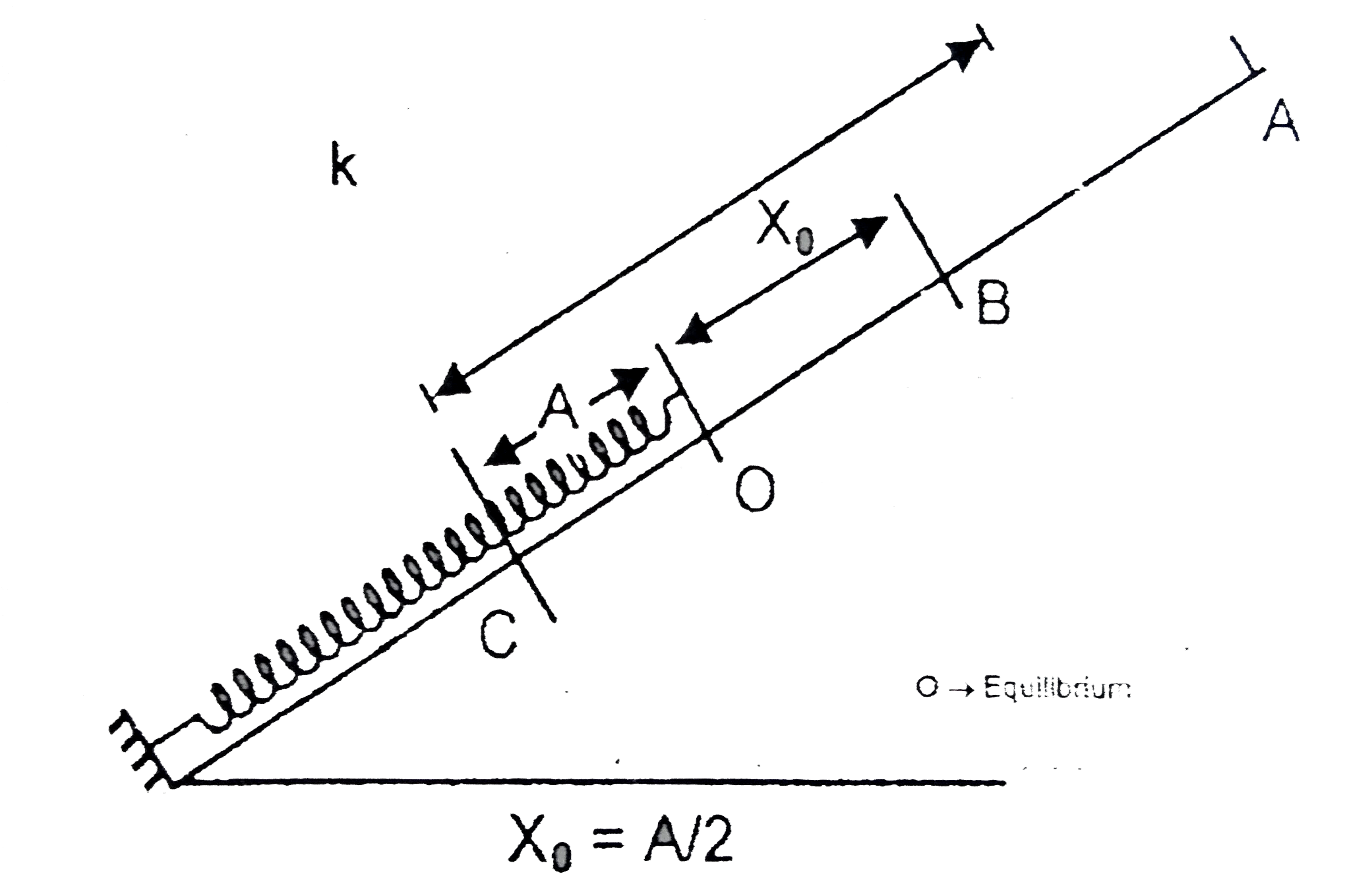
The motion from B to C and back to B can be regarded as motion of a particle performing SHM [from x=+A2 to negative extrem e and back to x=+A2]
Time for this motion can be obtained from fig given below.

Particle on circle moves from P1 to C to P2. Time required
for completing this two third circle =2T3
Hence, desired time t2=2T3=232π√mk
=4π3√401000l=8π30s=0.84s
∴ Time required for the block to come back to A is t=2t1+t0
=2×0.35+0.84=1.54s
Topper's Solved these Questions
Similar Questions
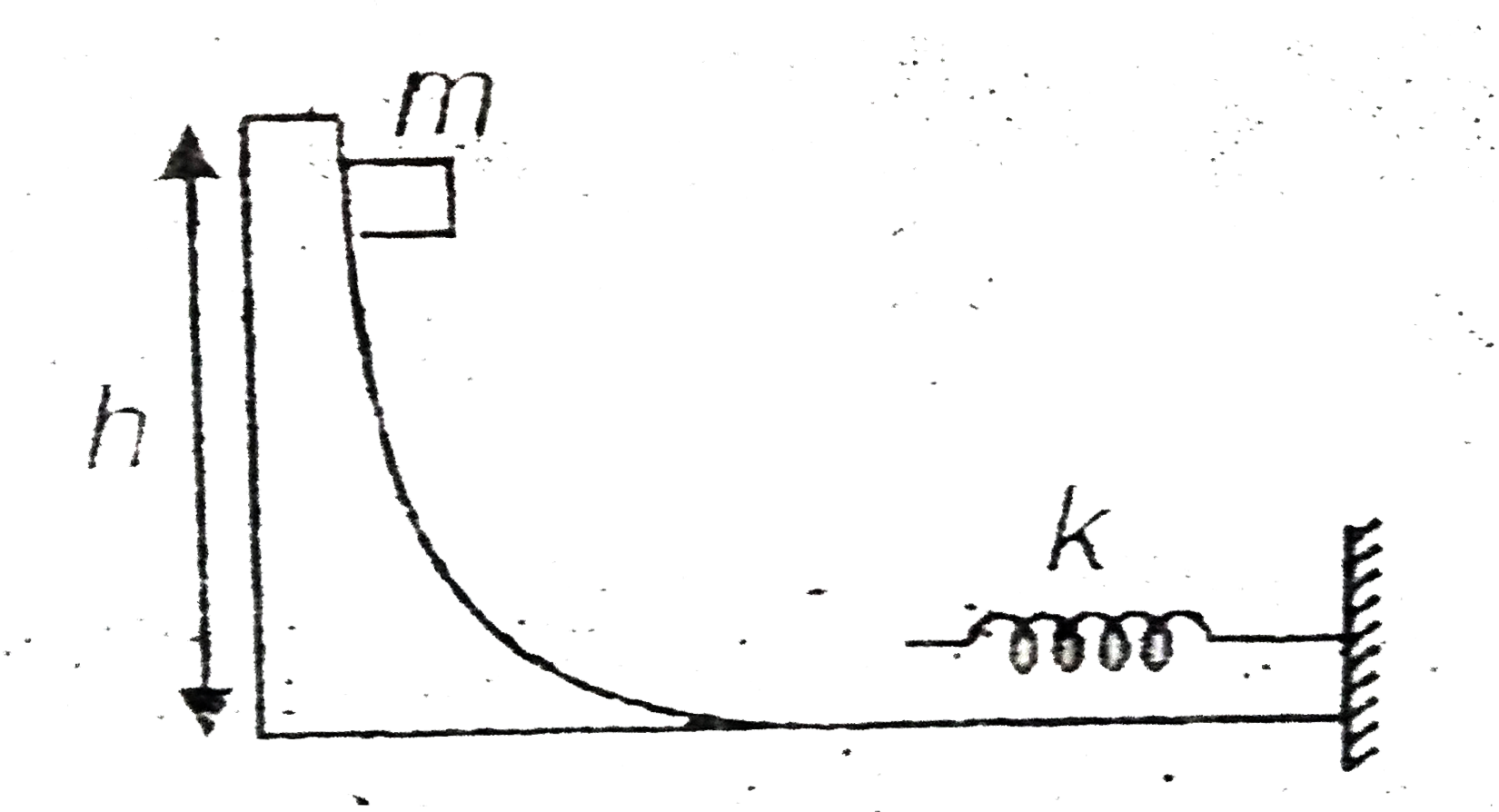
A block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
 View Solution
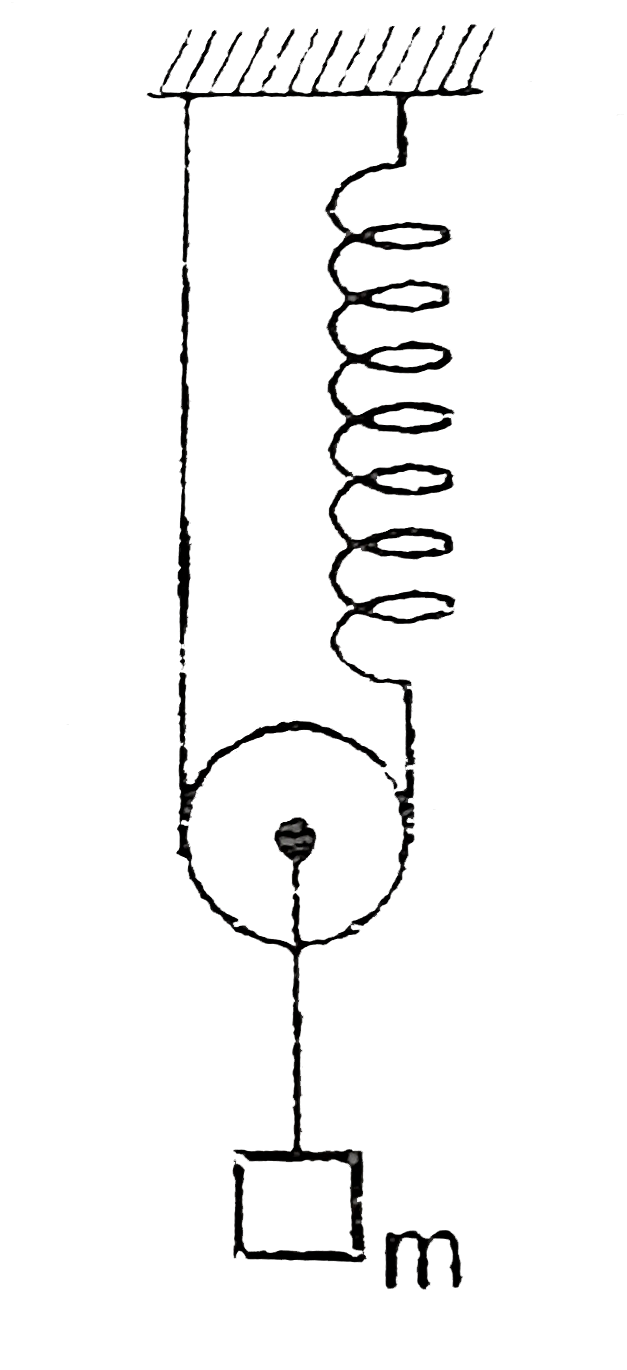
View SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
 View Solution
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is
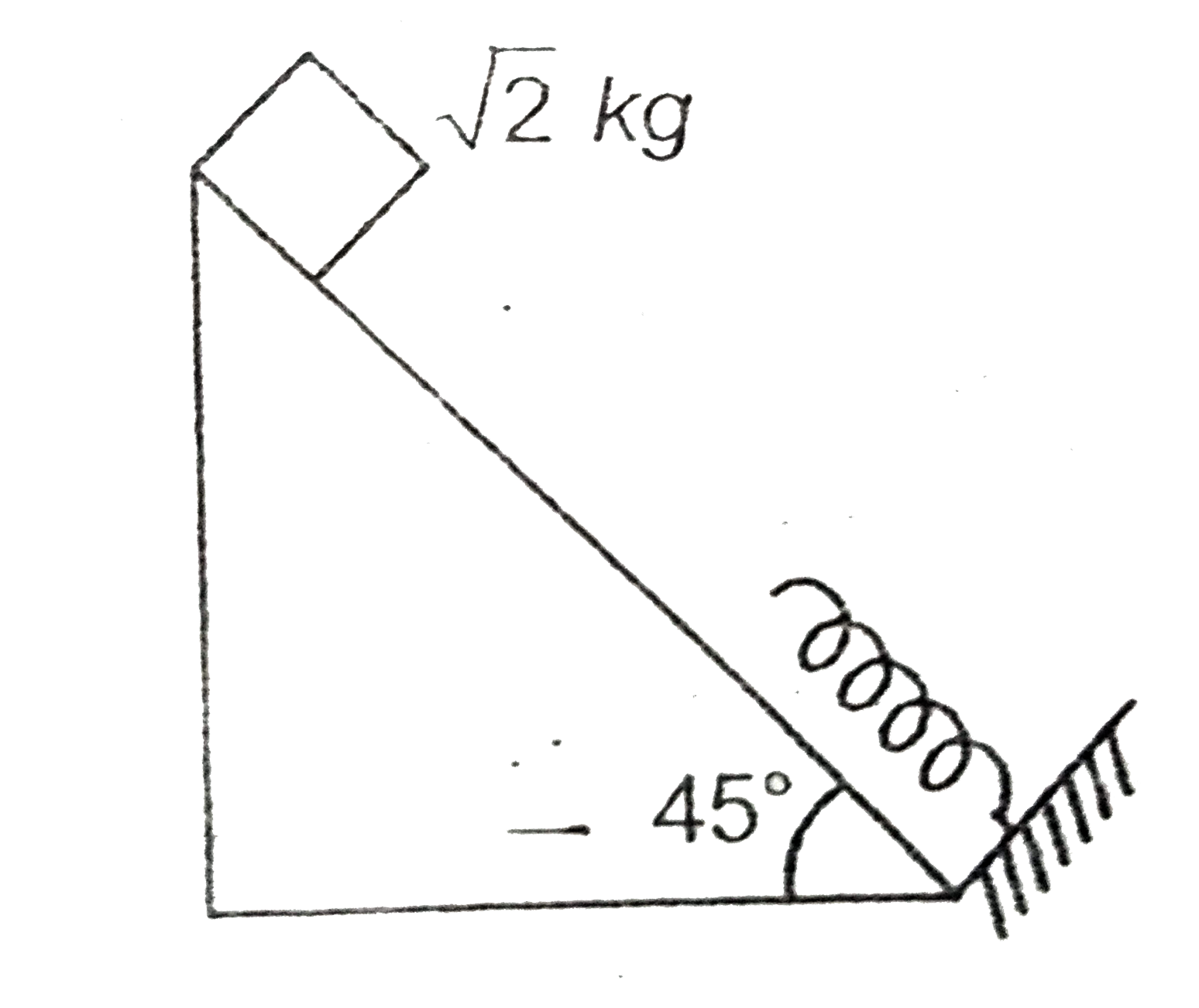 View Solution
View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is
 View Solution
View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100N/m and block comes to rest after compressing spring by 1 m, find the distance travelled by the block before it comes t o rest.
 View Solution
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest
 View Solution
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest
 View Solution
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionA block of mass m is relesed from rest from a height h onto a smooth surface of mass M fitted with an ideal spring of stiffness k. find the maximum compression in the spring.
 View Solution
View Solution

