Represent equation of an adiabatic process in terms of (i) T and V (ii) P and T.
The correct Answer is:(i) TVγ−1= constant (ii) Pγ−1Tγ= constant
To represent the equation of an adiabatic process in terms of (i) Temperature (T) and Volume (V) and (ii) Pressure (P) and Temperature (T), we can follow these steps:
Step 1: Understand the Adiabatic Process
In an adiabatic process, there is no heat transfer to or from the system, which means ΔQ=0. According to the first law of thermodynamics:
ΔQ=dU+dW
This implies that:
dU=−dW
Step 2: Use the Ideal Gas Law
For an ideal gas, the equation of state is given by:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the universal gas constant, and T is the temperature.
Step 3: Derive the Relation Between P and V
For an adiabatic process, the relation between pressure and volume is given by:
PVγ=constant
where γ=CpCv is the heat capacity ratio.
Step 4: Derive the Relation Between T and V
From the ideal gas law, we can express P in terms of T and V:
P=nRTV
Substituting this into the adiabatic equation:
(nRTV)Vγ=k
This simplifies to:
nRTVγ−1=k
Rearranging gives:
TVγ−1=knR
Thus, the relation between T and V for an adiabatic process is:
TVγ−1=constant
Step 5: Derive the Relation Between P and T
Now, we want to express the adiabatic condition in terms of P and T. From the ideal gas law, we can express V as:
V=nRTP
Substituting this into the adiabatic equation:
P(nRTP)γ=k
This simplifies to:
P(nRT)γPγ=k
Rearranging gives:
P1−γTγ=constant
Thus, the relation between P and T for an adiabatic process is:
PTγγ−1=constant
Final Relations:
1. In terms of T and V:
TVγ−1=constant
2. In terms of P and T:
PTγγ−1=constant
In an adiabatic process, there is no heat transfer to or from the system, which means ΔQ=0. According to the first law of thermodynamics:
ΔQ=dU+dW
This implies that:
dU=−dW
For an ideal gas, the equation of state is given by:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the universal gas constant, and T is the temperature.
For an adiabatic process, the relation between pressure and volume is given by:
PVγ=constant
where γ=CpCv is the heat capacity ratio.
From the ideal gas law, we can express P in terms of T and V:
P=nRTV
Substituting this into the adiabatic equation:
(nRTV)Vγ=k
This simplifies to:
nRTVγ−1=k
Rearranging gives:
TVγ−1=knR
Thus, the relation between T and V for an adiabatic process is:
TVγ−1=constant
Now, we want to express the adiabatic condition in terms of P and T. From the ideal gas law, we can express V as:
V=nRTP
Substituting this into the adiabatic equation:
P(nRTP)γ=k
This simplifies to:
P(nRT)γPγ=k
Rearranging gives:
P1−γTγ=constant
Thus, the relation between P and T for an adiabatic process is:
PTγγ−1=constant
1. In terms of T and V:
TVγ−1=constant
2. In terms of P and T:
PTγγ−1=constant
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Exercise-2
1 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -I
15 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -II
17 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
64 Videos
Similar Questions
Knowledge Check
The ideal gas equation for an adiabatic process is
APVγ=constantBTVγ+1=constantCPγ−1=constantDPγ+1T=constantTwo different adiabatic parts for the same gas intersect two isothermals at T1andT_2 as shown in P-V diagram . Then the ratio of VaVb will be
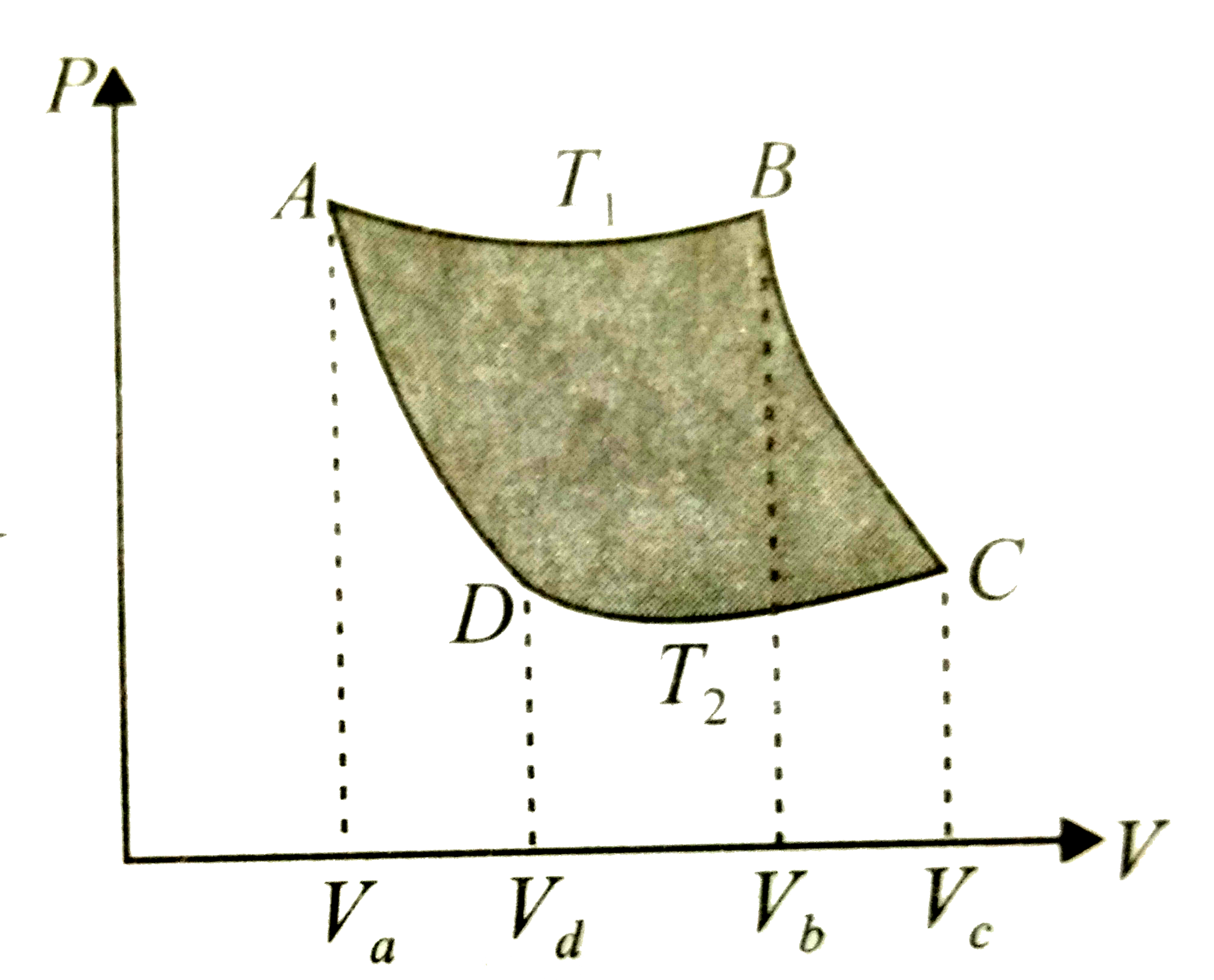 Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
Which equation is correct for adiabatic process ?
View SolutionAn ideal gas of adiabatic exponent γ is expanded so that the amount of heat transferred to the gas is equal to the decrease of its internal energy. Then, the equation of the process in terms of the variables T and V is
View SolutionDuring adiabatic process, pressure P and density equation is:
View SolutionDuring adiabatic process pressure (p) versus density (ρ) equation is
View SolutionShow that the slope of p−V diagram is greater for an adiabatic process as compared to an isothermal process.
View SolutionDefine an adiabatic process and state essential conditions for such a process to take place. Write its process equations in terms of , and . Show analytically that work done by one mole of an ideal gas during adiabatic expansion from temperature T1 to T2 is given by =R(T1−t2)1−λ.
View Solution
