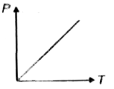
If ideal diatomic gas follows the process, as shown in graph, where $T$ is temperature in kelvin and $V$ is volume $(m^{3})$ , then molar heat capacity for this process will be [in terms of gas constant $R]$ :

A

$\frac{7 R}{2}$

B

$5 R$

C

$\frac{19 R}{6}$

D

$\frac{11 R}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$C = C v + \frac{R}{1 - η} \dots \dots . . (i)$
$T^{2} V^{- 3} =$ constant $, P V = n R T$
$P^{2} V^{2} V^{- 3} =$ constat $, P^{2} V^{- 1} =$ constant
$P V^{- 1 / 2} =$ constant
$N = - 1 / 2$
$C = \frac{5 R}{2} + \frac{2 R}{3} = \frac{19 R}{6}$

|

Updated on:21/07/2023

Class 11 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-KTG & THERMODYNAMICS-PART -I

Home
Ask Doubt
Profile