An ideal gas can be expanded form an initial state to a certain volume through two different processes PV2= constant and (ii) P=KV2 where K is a positive constant. Then
Final temperature in (i) will be greater than in (ii)
Final temperature in (ii) will be greater than (i)
Total heat given to the gas in (i) case is greater than in (ii)
Total heat given to the gas in (ii) case is greater than in (i)
The correct Answer is:B, D
To solve the problem step by step, we will analyze the two processes given for the expansion of an ideal gas and determine the relationship between the final temperatures and the total heat given to the gas in each case.
Step 1: Analyze the first process PV2=constant
1. Start with the equation for the first process:
PV2=K(where K is a constant)
2. From the ideal gas equation, we know:
PV=nRT
Rearranging gives:
P=nRTV
3. Substitute P into the first process equation:
(nRTV)V2=K
Simplifying this, we get:
nRTV=K
4. Rearranging gives:
TV=KnR(constant)
This implies:
T∝1V(Temperature is inversely proportional to Volume)
5. Since the gas is expanding (volume is increasing), the temperature T will decrease.
Step 2: Analyze the second process P=KV2
1. Start with the equation for the second process:
P=KV2
2. Again, using the ideal gas equation:
PV=nRT⇒P=nRTV
3. Substitute P into the second process equation:
nRTV=KV2
Rearranging gives:
nRT=KV3
4. Rearranging gives:
T=KV3nR(Temperature is directly proportional to the cube of Volume)
5. Since the gas is expanding (volume is increasing), the temperature T will increase.
Step 3: Compare the final temperatures
From the analysis:
- In the first process, as the volume increases, the temperature decreases.
- In the second process, as the volume increases, the temperature increases.
Thus, we conclude:
T2>T1(Final temperature in the second process is greater than in the first)
Step 4: Total heat given to the gas
1. The total heat Q given to the gas can be related to the change in temperature and the specific heat capacity.
2. Since the temperature in the second process is higher than in the first, it can be inferred that the total heat given to the gas in the second process is greater than in the first process.
Final Conclusion
- The final temperature in the second process is greater than in the first process.
- The total heat given to the gas in the second process is greater than in the first process.
PV2=K(where K is a constant)
2. From the ideal gas equation, we know:
PV=nRT
Rearranging gives:
P=nRTV
(nRTV)V2=K
Simplifying this, we get:
nRTV=K
TV=KnR(constant)
This implies:
T∝1V(Temperature is inversely proportional to Volume)
P=KV2
PV=nRT⇒P=nRTV
nRTV=KV2
Rearranging gives:
nRT=KV3
T=KV3nR(Temperature is directly proportional to the cube of Volume)
- In the first process, as the volume increases, the temperature decreases.
- In the second process, as the volume increases, the temperature increases.
T2>T1(Final temperature in the second process is greater than in the first)
2. Since the temperature in the second process is higher than in the first, it can be inferred that the total heat given to the gas in the second process is greater than in the first process.
- The total heat given to the gas in the second process is greater than in the first process.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -IV9videos
KTG & THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Exercise-31videos
KTG & THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -I15videos
KTG & THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise64videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise64videos
MAGNETIC FIELD AND FORCES
Similar Questions
An ideal gas can be taken form initial state 1 to final state 2 by two different process. Let ΔQ and W represent the heat given and work done by the system. Then which quantities is/are same in both process (where ΔU= internal energy of gas)
View SolutionAn ideal gas expands in such a way that PV2=constant throughout the process.
View SolutionAn ideal gas expands according to the law PV3/2=constant We conclude that
View Solution0.5 litre of an ideal gas at a pressure of 20 atm expands to a final volume of 0.5m3. The process obeys the equation PV = a constant, (i) Find the value of this constant (ii) What is the final pressure ? And (iii) Find, the work done by the gas,
View SolutionAn ideal gas expands in such a manner that its pressure and volume can be related by equation PV2= constant. During this process, the gas is
View SolutionIn the process pV2= constant, if temperature of gas is increased, then
View SolutionTemperature of an ideal gas is 300 K . The final temperature of the gas when its volume changes from V to 2V in the process p=αV (here α is a positive constant) is
View SolutionTemperature of an ideal gas is 300 K. The change in temperature of the gas when its volume changes from V to 2V in the process p = aV (Here, a is a positive constant) is
View SolutionP-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
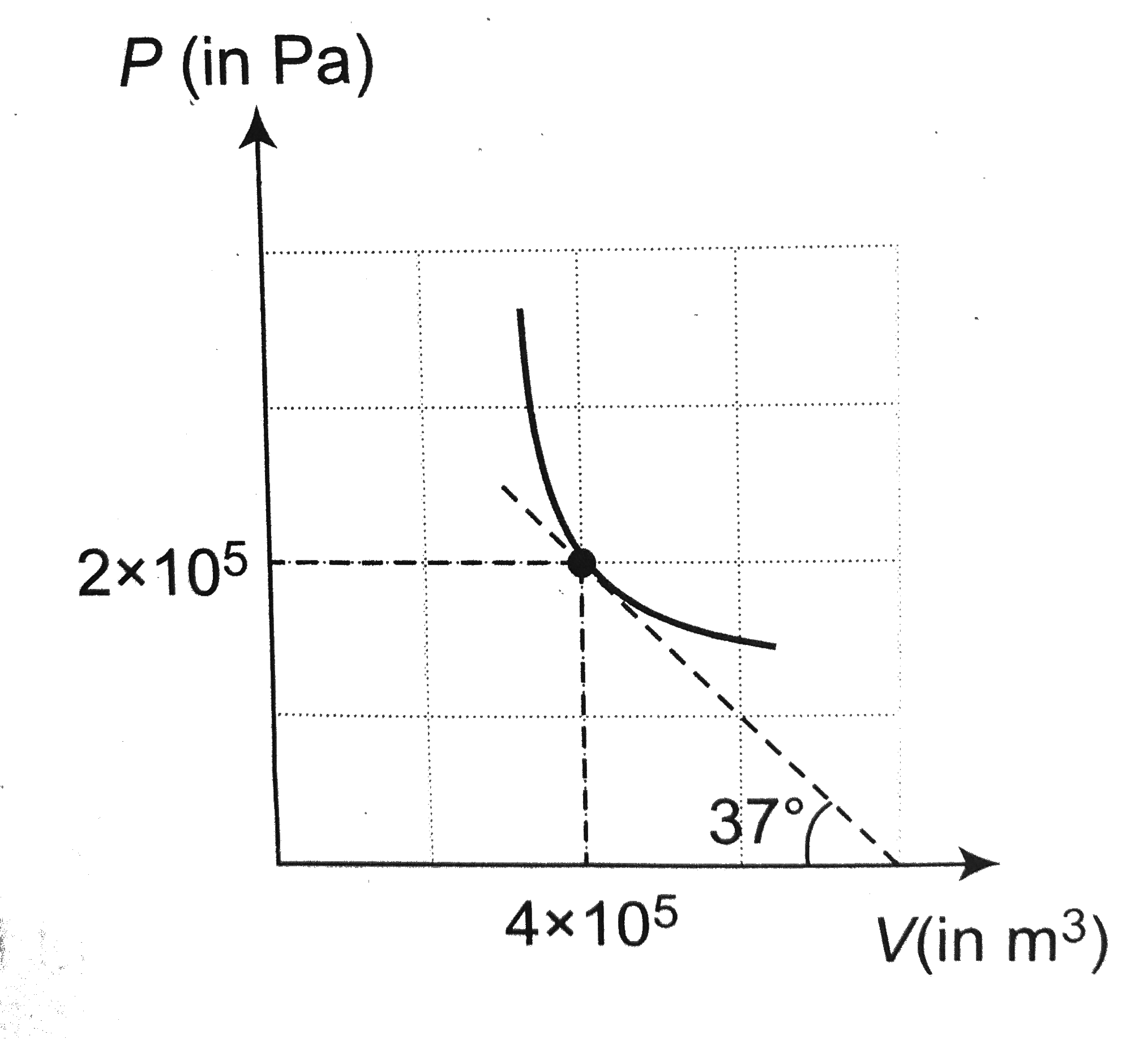 View Solution
View SolutionThe internal energy of a certain substance is given by the following equation :
U=3 PV+84
where U is given in kJ/kg, P is in kPa, and V is in m3/kg
A system composed of 3 kg of this substance expands from an initial pressure of 400 kPa and a volume of A 0.2m3 to a final pressure 100 kPa in a process in which pressure and volume are related by PV2=constant.
In another process the same system expands according to the same pressure-volume relationship as in above question, but from the same initial state of the final state as in above question, but the heat transfer in this case is +30 kJ.Then the work transfer for this process is :View Solution

