A thermally isolated vessel contains 100g of water at 0∘C when air above the water is pumped out, some of the water freezes and some evaporates at 0∘C itself. Calculate the mass at 0∘C=2.10×106j/kg and latent heat of fusion of ice =3.36×105j/kg.
86.2g
13.8g
76.2g
65.6g
The correct Answer is:A
To solve the problem, we will use the principle of calorimetry, which states that the total heat lost by the water that freezes is equal to the total heat gained by the water that evaporates.
1. Define Variables:
- Let m1 be the mass of water that freezes (in kg).
- The total mass of water is given as 100g=0.1kg.
- Therefore, the mass of water that evaporates will be 0.1−m1.
2. Heat Loss by Freezing:
- The heat lost when m1 kg of water freezes can be calculated using the formula:
Qloss=m1×Lf
- Where Lf=3.36×105J/kg (latent heat of fusion).
3. Heat Gain by Evaporation:
- The heat gained when 0.1−m1 kg of water evaporates can be calculated using the formula:
Qgain=(0.1−m1)×Lv
- Where Lv=2.10×106J/kg (latent heat of vaporization).
4. Set Up the Equation:
- According to the principle of calorimetry:
Qloss=Qgain
- This gives us:
m1×Lf=(0.1−m1)×Lv
5. Substitute Values:
- Substitute Lf and Lv into the equation:
m1×(3.36×105)=(0.1−m1)×(2.10×106)
6. Expand and Rearrange:
- Expanding the right side:
3.36×105m1=0.1×2.10×106−2.10×106m1
- This simplifies to:
3.36×105m1+2.10×106m1=0.1×2.10×106
7. Factor Out m1:
- Factor out m1:
m1(3.36×105+2.10×106)=0.1×2.10×106
8. Calculate the Coefficient:
- Calculate 3.36×105+2.10×106:
3.36×105+2.10×106=2.43×106
9. Solve for m1:
- Now, substitute back into the equation:
m1(2.43×106)=0.1×2.10×106
- Thus:
m1=0.1×2.10×1062.43×106
- Calculate m1:
m1=0.21×1062.43×106≈0.0862kg=86.2g
Final Answer:
The mass of the water that freezes is approximately 86.2 g.
- Let m1 be the mass of water that freezes (in kg).
- The total mass of water is given as 100g=0.1kg.
- Therefore, the mass of water that evaporates will be 0.1−m1.
- The heat lost when m1 kg of water freezes can be calculated using the formula:
Qloss=m1×Lf
- Where Lf=3.36×105J/kg (latent heat of fusion).
- The heat gained when 0.1−m1 kg of water evaporates can be calculated using the formula:
Qgain=(0.1−m1)×Lv
- Where Lv=2.10×106J/kg (latent heat of vaporization).
- According to the principle of calorimetry:
Qloss=Qgain
- This gives us:
m1×Lf=(0.1−m1)×Lv
- Substitute Lf and Lv into the equation:
m1×(3.36×105)=(0.1−m1)×(2.10×106)
- Expanding the right side:
3.36×105m1=0.1×2.10×106−2.10×106m1
- This simplifies to:
3.36×105m1+2.10×106m1=0.1×2.10×106
- Factor out m1:
m1(3.36×105+2.10×106)=0.1×2.10×106
- Calculate 3.36×105+2.10×106:
3.36×105+2.10×106=2.43×106
- Now, substitute back into the equation:
m1(2.43×106)=0.1×2.10×106
- Thus:
m1=0.1×2.10×1062.43×106
- Calculate m1:
m1=0.21×1062.43×106≈0.0862kg=86.2g
The mass of the water that freezes is approximately 86.2 g.
Topper's Solved these Questions
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-2
1 Videos
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercie-3
1 Videos
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-1
1 Videos
- CALORIMETRYBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise
19 Videos
- CAPACITORBOOK - RESONANCE ENGLISHCHAPTER - CAPACITOREXERCISE - Exercise
45 Videos
Similar Questions
A thermally isolated vessel contains 100g of water at 0∘C. When air above the water is pumped out, some of the water freezes and some evaporates at 0∘C itself. Calculate the mass of the ice formed such that no water is left in the vessel. Latent heat of vaporization of water at 0∘C=2.10×106J/kg and latent heat of fusion of ice =3.36×105J/kg.
View SolutionA thermally insulated vessel contains 150g of water at 0∘C. Then the air from the vessel is pumped out adiabatically. A fraction of water turms into ice and the rest evaporates at 0∘C itself. The mass of evaporated water will be closest to :
(Latent heat of vaporization of water =2.10×106jkg−1 and Latent heat of Fusion of water =3.36×105jkg−1)
View Solution
Knowledge Check
If 10 g of ice is added to 40 g of water at 15∘C, then the temperature of the mixture is (specific heat of water =4.2×103jkg−1K−1, Latent heat of fusion of ice =3.36×105jkg−1)
A15∘CB12∘CC102CD0∘C
A thermal insulated vessel contains some water at 0∘C. The vessel is connected to a vaccum pump to pum out water vapour. This results in some water getting frozen. It is given latent heat of vaporization of water at 0∘C=21×105J/kg and latent heat of freezing of water =3.36×105J/kg. the maximum percentage amount of water vapour that will be solidified in this manner will be:
View SolutionA closely thermally insulated vessel contains 100 g of water at 0∘C. If the air from this vessel is rapidly pumped out, intensive evaporation will produce cooling and as a result of this, water freeze. How much ice will be formed by this method? If latent heat of fusion is 80cal/g and of evaporation 560cal/g .
[ Hint If m gram ice is formed, mLf=(100−m)lv]
View SolutionA calorimeter of mass 60 g contains 180 g of water at 29∘C. Find the final temperature of the mixture, when 37.2 g of ice at -10∘C is added to it (specific heat capacity of water = 4200J/kgK. latent heat of ice 336×103J/kg. Specific heat capacity of ice =2100J/kgK, specific heat capacity of the calorimeter is 0.42Jg−1×C−1)
View SolutionA piece of ice of mass 100g and at temperature 0∘C is put in 200g of water of 25∘C. How much ice will melt as the temperature of the water reaches 0∘C ? (specific heat capacity of water =4200Jkg−1K−1 and latent heat of fusion of ice =3.4×105JKg−1).
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution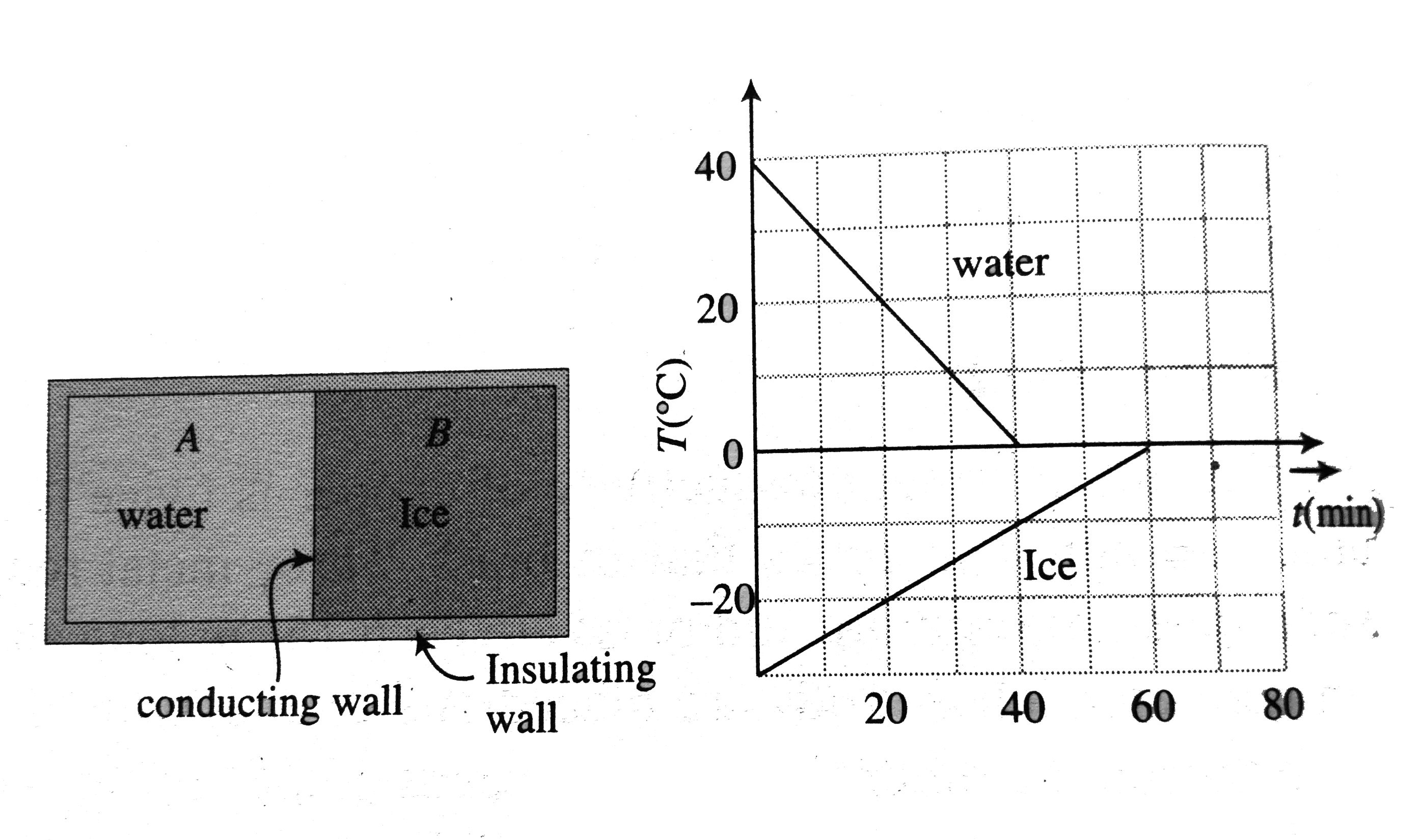
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The value of rate P is?
View Solution
