Two particles at a distance apart, are thrown towards each other on an inclined smooth plane with equal speed 'v'. Inclined plane is inclined at an angle of with the horizontal. It is known that both particle move along the same straight line. The particle colllide at the point from where the lower is thrown. Find the value of velocity.
The correct Answer is:A
To solve the problem, we need to analyze the motion of two particles thrown towards each other on an inclined plane. Let's break down the solution step by step.
Step 1: Understand the setup
We have two particles, A and B, starting 5 meters apart on a smooth inclined plane that is inclined at an angle of 30∘ with the horizontal. Both particles are thrown towards each other with the same initial speed v.
Step 2: Identify the forces acting on the particles
The only force acting on the particles is gravity. The component of gravitational acceleration acting along the incline is given by:
gincline=gsin(θ)
where g=10m/s2 and θ=30∘. Thus,
gincline=10sin(30∘)=10×12=5m/s2
Step 3: Determine the time taken for each particle to reach the point of collision
Let’s denote the time taken for particle A to reach the collision point as tA and for particle B as tB. Since both particles are thrown with the same speed and collide at the midpoint, we have:
tA=tB=t
Step 4: Use the equations of motion
For particle A moving up the incline:
sA=vt−12ginclinet2
For particle B moving down the incline:
sB=vt−12ginclinet2
Since the total distance between them is 5 m, we have:
sA+sB=5
Substituting the equations for sA and sB:
(vt−12ginclinet2)+(vt−12ginclinet2)=5
2(vt−12ginclinet2)=5
2vt−ginclinet2=5
Step 5: Substitute gincline
Substituting gincline=5m/s2:
2vt−5t2=5
Step 6: Rearrange the equation
Rearranging gives us:
5t2−2vt+5=0
Step 7: Solve for t
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=5, b=−2v, and c=5:
t=2v±√(−2v)2−4⋅5⋅52⋅5
t=2v±√4v2−10010
Step 8: Set the discriminant to zero for collision
For the particles to collide, the discriminant must be zero:
4v2−100=0⟹4v2=100⟹v2=25⟹v=5m/s
Conclusion
The value of the velocity v is 5m/s.
We have two particles, A and B, starting 5 meters apart on a smooth inclined plane that is inclined at an angle of 30∘ with the horizontal. Both particles are thrown towards each other with the same initial speed v.
The only force acting on the particles is gravity. The component of gravitational acceleration acting along the incline is given by:
gincline=gsin(θ)
where g=10m/s2 and θ=30∘. Thus,
gincline=10sin(30∘)=10×12=5m/s2
Let’s denote the time taken for particle A to reach the collision point as tA and for particle B as tB. Since both particles are thrown with the same speed and collide at the midpoint, we have:
tA=tB=t
For particle A moving up the incline:
sA=vt−12ginclinet2
For particle B moving down the incline:
sB=vt−12ginclinet2
Since the total distance between them is 5 m, we have:
sA+sB=5
Substituting the equations for sA and sB:
(vt−12ginclinet2)+(vt−12ginclinet2)=5
2(vt−12ginclinet2)=5
2vt−ginclinet2=5
Substituting gincline=5m/s2:
2vt−5t2=5
Rearranging gives us:
5t2−2vt+5=0
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=5, b=−2v, and c=5:
t=2v±√(−2v)2−4⋅5⋅52⋅5
t=2v±√4v2−10010
For the particles to collide, the discriminant must be zero:
4v2−100=0⟹4v2=100⟹v2=25⟹v=5m/s
The value of the velocity v is 5m/s.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 273videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 287videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 255videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
 View Solution
View SolutionThe maximum range of a projectile is 500m. If the particle is thrown up a plane is inclined at an angle of 30∘ with the same speed, the distance covered by it along the inclined plane will be:
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
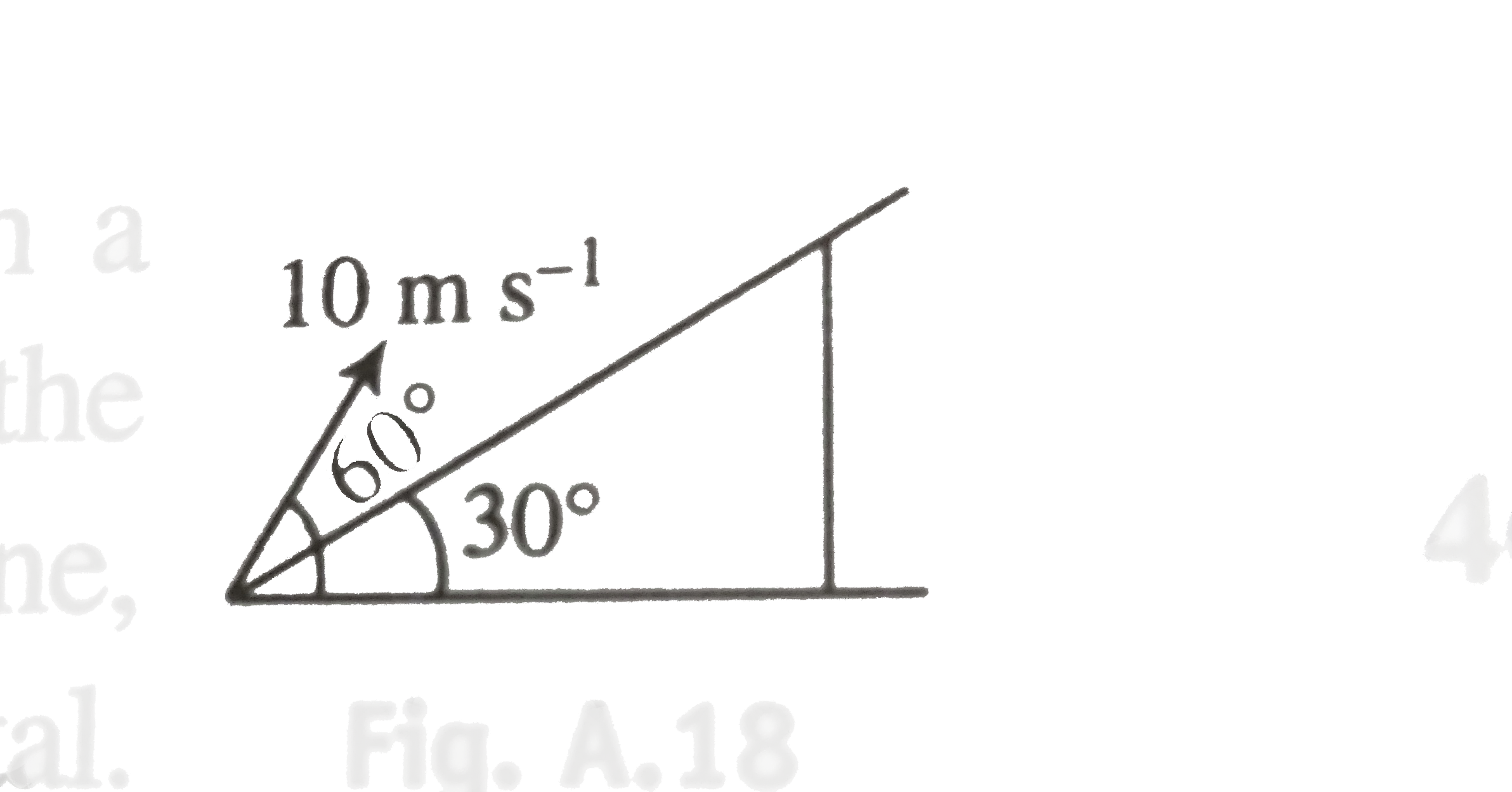 View Solution
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
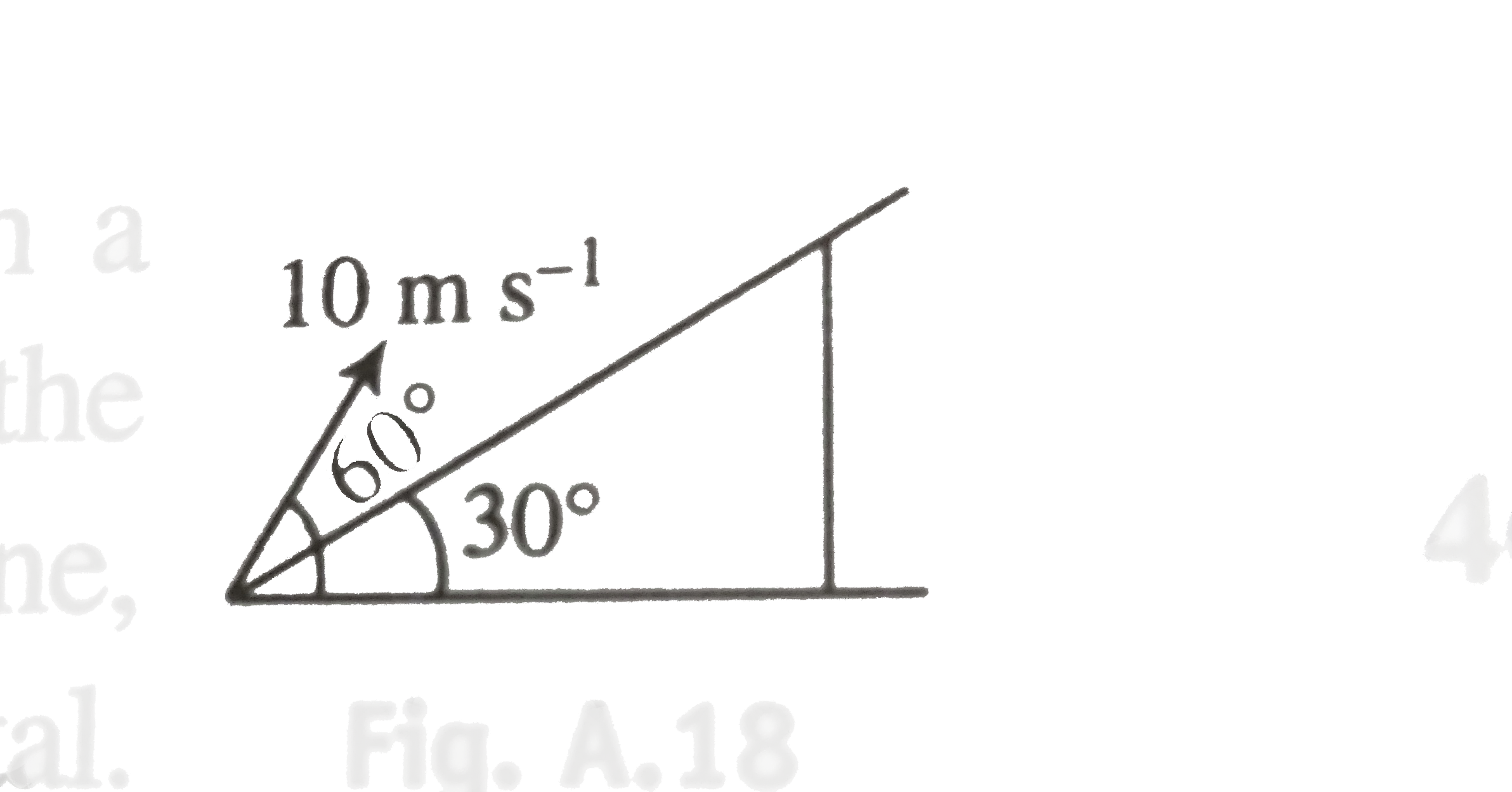 View Solution
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
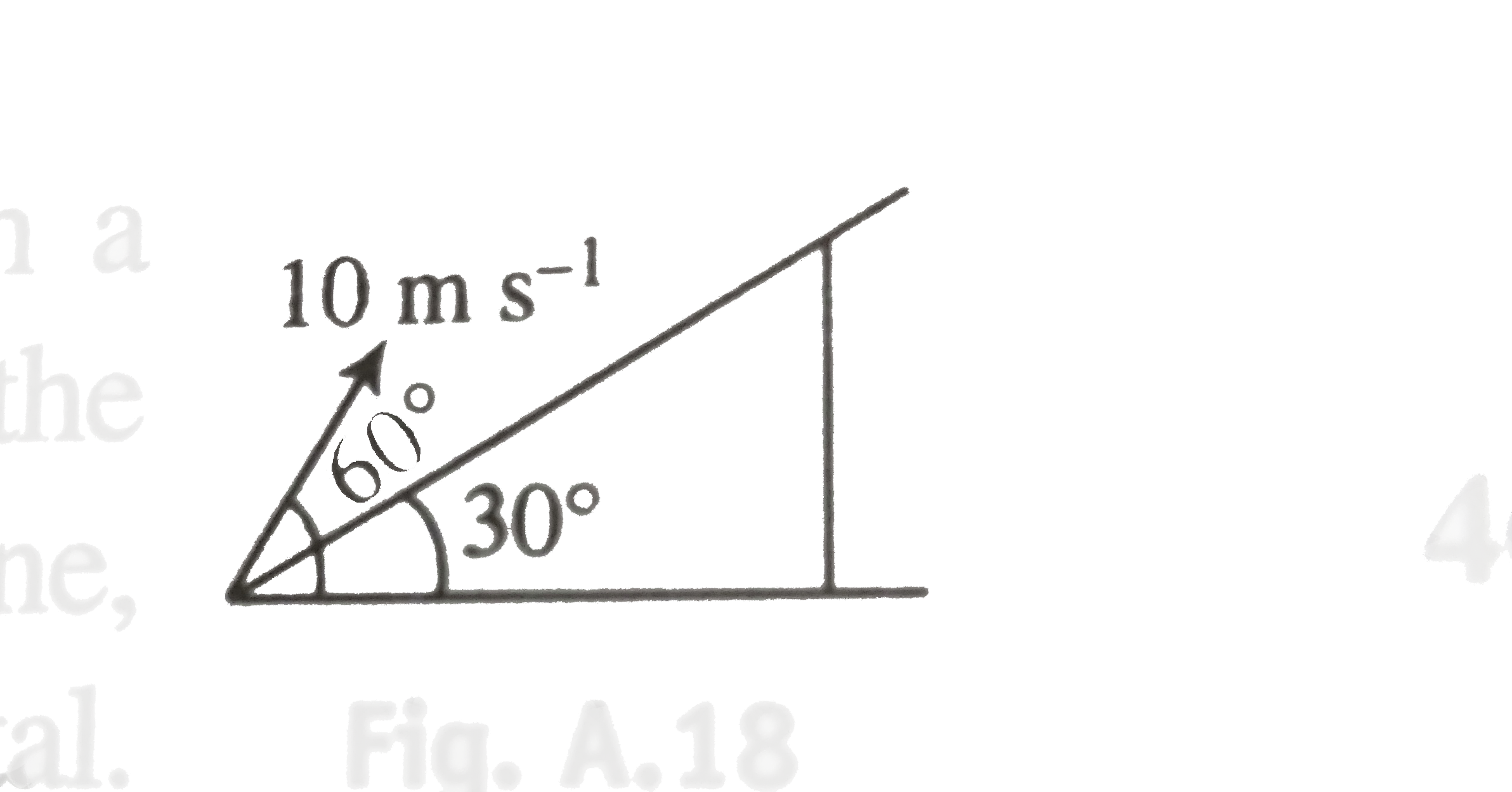 View Solution
View SolutionA particle of mass m attached to a string of length l is descending circular motion on a smooth plane inclined at an angle α with the horizontal. For the particle to reach the highest point its velocity at the lowest point should exceed.
View SolutionA particle is projected along the line of greatest slope up a rough plane inclined at an angle of 45∘ with the horizontal. If the coefficient of friction is 1/2 . Their retardation is:
View SolutionA particle is projected along the line of greatest slope up a rough plane inclined at an angle of 45∘ with the horizontal. If the coefficient of friction is 1/2 . Their retardation is:
View SolutionIn figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 . View Solution
. View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View Solution

