A particle is projected from a point (0,1) of Y-axis (assume + Y direction vertically upwards) aiming towards a point (4,9). It fell on ground along x axis in 1 sec. Taking g=10ms2 and all coordinate in metres. Find the X-coordinate where it fell.
93,0)
(4,0)
(2,0)
(2√5,0)
The correct Answer is:C
To solve the problem step by step, we will follow the physics of projectile motion and the given conditions.
Step 1: Understand the Problem
A particle is projected from the point (0, 1) aiming towards the point (4, 9) and falls on the ground (x-axis) after 1 second. We need to find the x-coordinate where it fell.
Step 2: Determine the Slope
To find the angle of projection, we first calculate the slope of the line connecting the points (0, 1) and (4, 9).
slope=y2−y1x2−x1=9−14−0=84=2
Thus, we have:
tanθ=2
Step 3: Use the Time of Flight
The time of flight t is given as 1 second. The vertical motion can be analyzed using the equation of motion:
s=ut+12at2
Where:
- s is the vertical displacement (final position - initial position)
- u is the initial vertical velocity component
- a is the acceleration (which is −g, with g=10m/s2)
- t is the time of flight
Step 4: Calculate the Vertical Displacement
The particle starts at (0, 1) and falls to the ground (y = 0). Therefore, the vertical displacement s is:
s=0−1=−1m
Step 5: Substitute Values into the Equation
Substituting the known values into the equation:
−1=uy⋅1+12(−10)⋅(12)
This simplifies to:
−1=uy−5
Rearranging gives:
uy=4m/s
Step 6: Find the Horizontal Component
Now, we need to find the horizontal component of the initial velocity ux. We know:
tanθ=uyux
From the slope, we have:
tanθ=2⟹4ux=2
Solving for ux:
ux=42=2m/s
Step 7: Calculate the X-coordinate
The x-coordinate where the particle falls can be calculated using:
x=ux⋅t
Substituting the values:
x=2⋅1=2m
Conclusion
The x-coordinate where the particle fell is:
2
---
A particle is projected from the point (0, 1) aiming towards the point (4, 9) and falls on the ground (x-axis) after 1 second. We need to find the x-coordinate where it fell.
To find the angle of projection, we first calculate the slope of the line connecting the points (0, 1) and (4, 9).
The time of flight t is given as 1 second. The vertical motion can be analyzed using the equation of motion:
- s is the vertical displacement (final position - initial position)
- u is the initial vertical velocity component
- a is the acceleration (which is −g, with g=10m/s2)
- t is the time of flight
The particle starts at (0, 1) and falls to the ground (y = 0). Therefore, the vertical displacement s is:
Substituting the known values into the equation:
Now, we need to find the horizontal component of the initial velocity ux. We know:
The x-coordinate where the particle falls can be calculated using:
The x-coordinate where the particle fell is:
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 27
3 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 28
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 25
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Two lines cut on the axis of x intercepts 4and−4 and on the axis of y intercepts 2 and 6 respectively. Find the coordinates of their point of intersection.
View Solution
A particle is projected from the horizontal x-z plane, in vertical x-y plane where x-axis is horizontal and positive y-axis vertically upwards. The graph of y coordinate of the particle v/s time is as shown . The range of the particle is √3. Then the speed of the projected particle is:
View SolutionA particle of mass m is released in vertical plane from a point P at x=x0 on the x-axis. It falls vertically parallel to the y-axis. Find the torque τ acting on the particle at a time about origin.

View SolutionTwo particles are moving along x-axis. Particle-1 starts from x=−10m with velocity 4m/s along negative x-direction and acceleration 2m/s2 along positive x-direction. Particle-2 starts from x=+2m with velocity 6m/s along positive x-direction and acceleration 2m/s2 along negative x-direction.
(a) Find the time when they collide.
(b) Find the x-coordinates where they collide. Both start simultaneously.
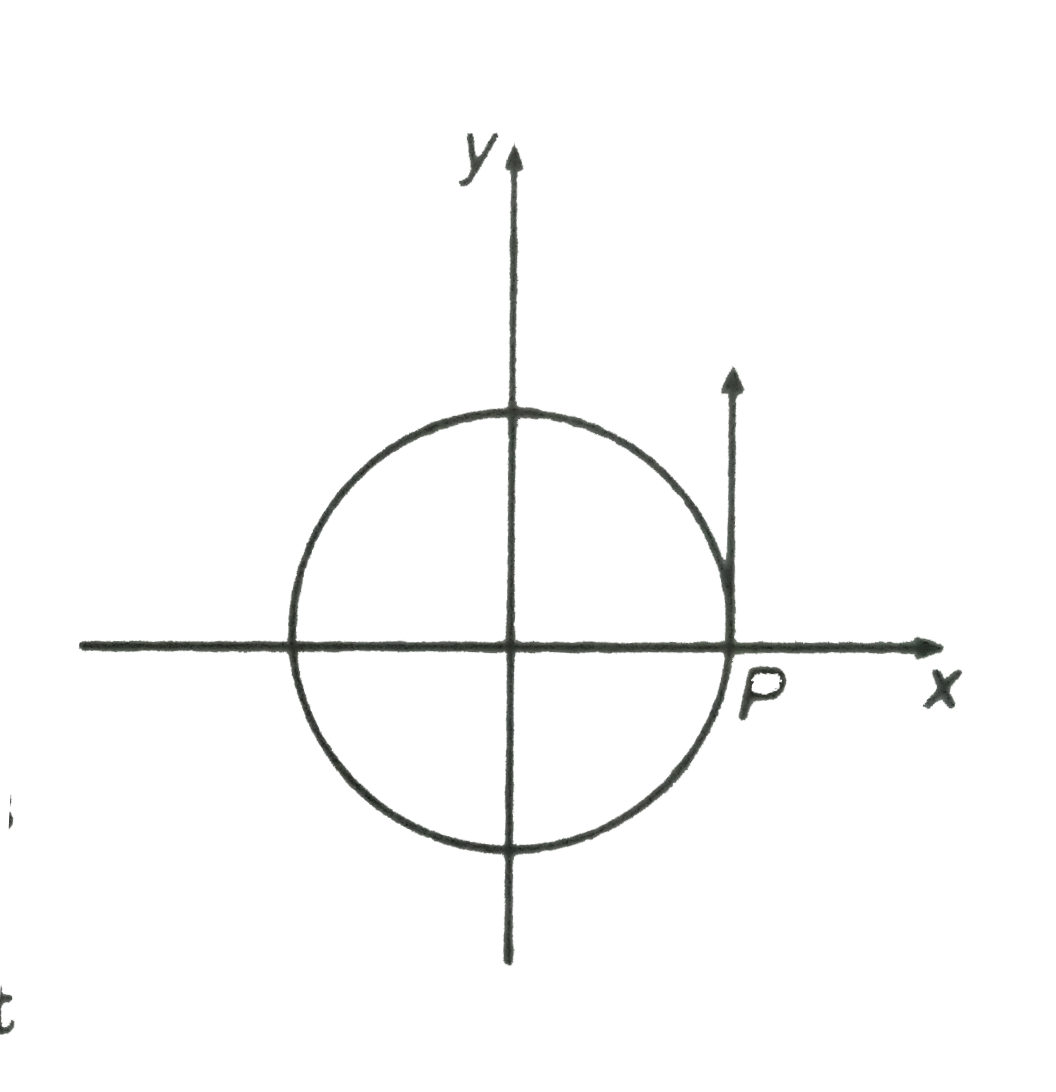
View SolutionA train is moving with a constant speed of 10m/s in a circle of radius 16πm. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed 10m/s relative to train towards negative x-axis at an angle of 37∘ with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g =10m/s2,sin37∘=35
View SolutionA particle is projected horizontally with spee u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g =10m/s2]
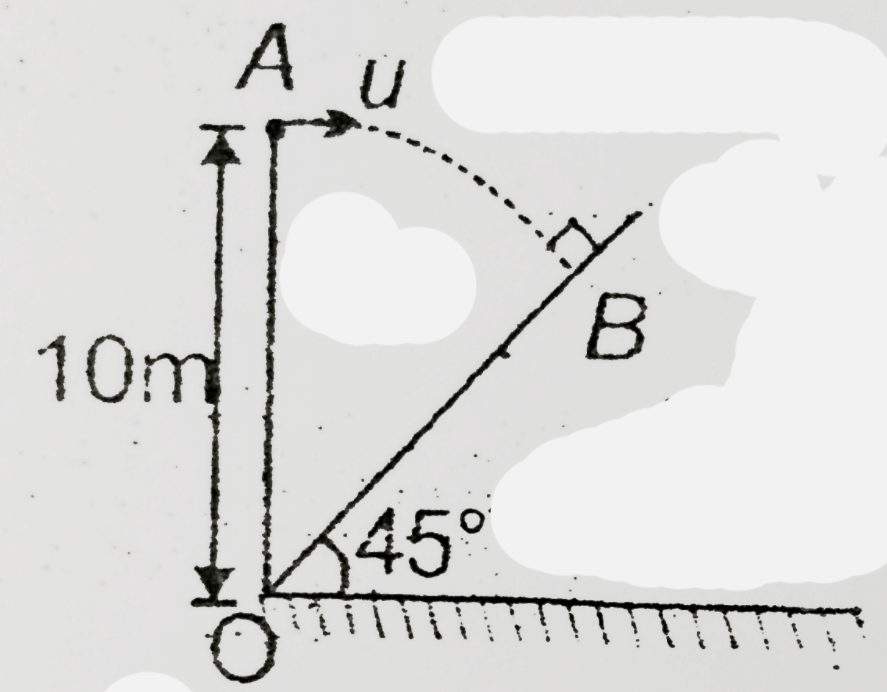
Find the length OB along the inclined plane
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionTaking horizontal ground as xz- plane and y-axis vertically upwards. A particle is projected from the horizontal ground from a point whose position vector is ˆi+ˆk meter with initial velocity 2i +3j+k from the origin when it hits ground is given by 15[11ˆi+nˆk], find n. (Take g=10m/s2 in negative y - direction)
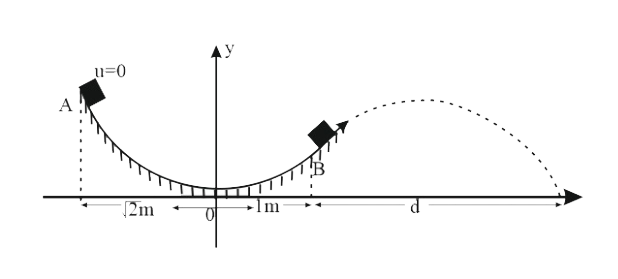
View SolutionA small body is released from point A of smooth parabolic path y=x2, where y is vertical axis and x is horizontal axis at ground, as shown. The body leaves the surface from point B. If g=10ms−2 then what is the value of d (in m)?
View SolutionFind the equation of a curve passing through the point (0,1) if the slope of the tangent to the curve at any point (x,y) is equal to the sum of the x coordinate (abscissa) and the product of the x coordinate and y coordinate (ordinate) of that point.
View Solution
