The blocks ov mass m1=1kg and m2=2kg are connected by an ideal spring, rest on a rough horizontal surface. The spring is unstressed. The spring constant of spring is K=2N/m. The coefficient of friction between blocks and horizontal surface is μ=12. Now the left block is imparted a velocity u towards right as shown. The largest value of u( in m/s) such that the block of mass m2 never moves is ( Take g=10m/s2)
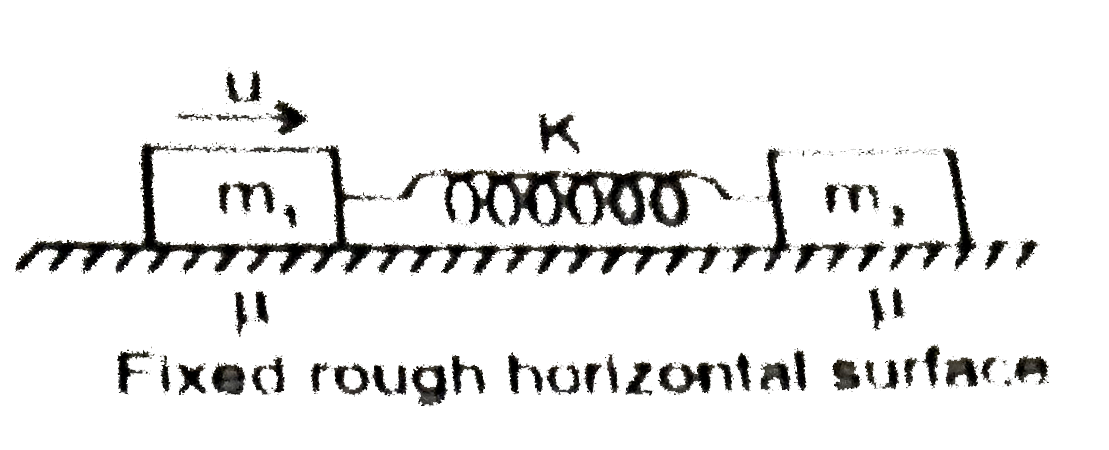
The correct Answer is:1−m/s
For the block of mass m2, not to move, the maximum compression in the spring x0 should be such that
kx0=μm2g…..(1)
Applying work energy theorem to block of mass m1 we get
12m1u2=12μ2m22g2K+μ2+m1m2g2K putting the appropriate value we get u=10m/s.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 39
3 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 40
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp 37
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Two objects are moving along the same straight line. They cross a point A With an acceleration a, 2a and velocity 2u, u at time t=0. The distance moved by the object when one overtakes the
View SolutionFor a particle undergoing rectilinear motion with uniform acceleration, the magnitude of displacement is one third the distance covered in some time interval. The magnitude of final velocity is less than magnitude of initial velocity for this time interval. Then the rationof initial speed to the final for this time interval is :
View SolutionIn the track shown in figure section AB is a quadrant of a circle of 1 metre radius. A block is released at A and slides without friction until it reaches B. After B it moves on a rough horizontal floor and comes to rest at distance 3 metres from B. What is the coefficient of friction between floor and body ?

View SolutionSpecific resistance of a wire depends on the
View SolutionA wire loaded by a weight of density 7.8g/cc is found to be of length 100cm. On immersing the weight in water. The length decrease by 0.20 cm find the original length of the wire.
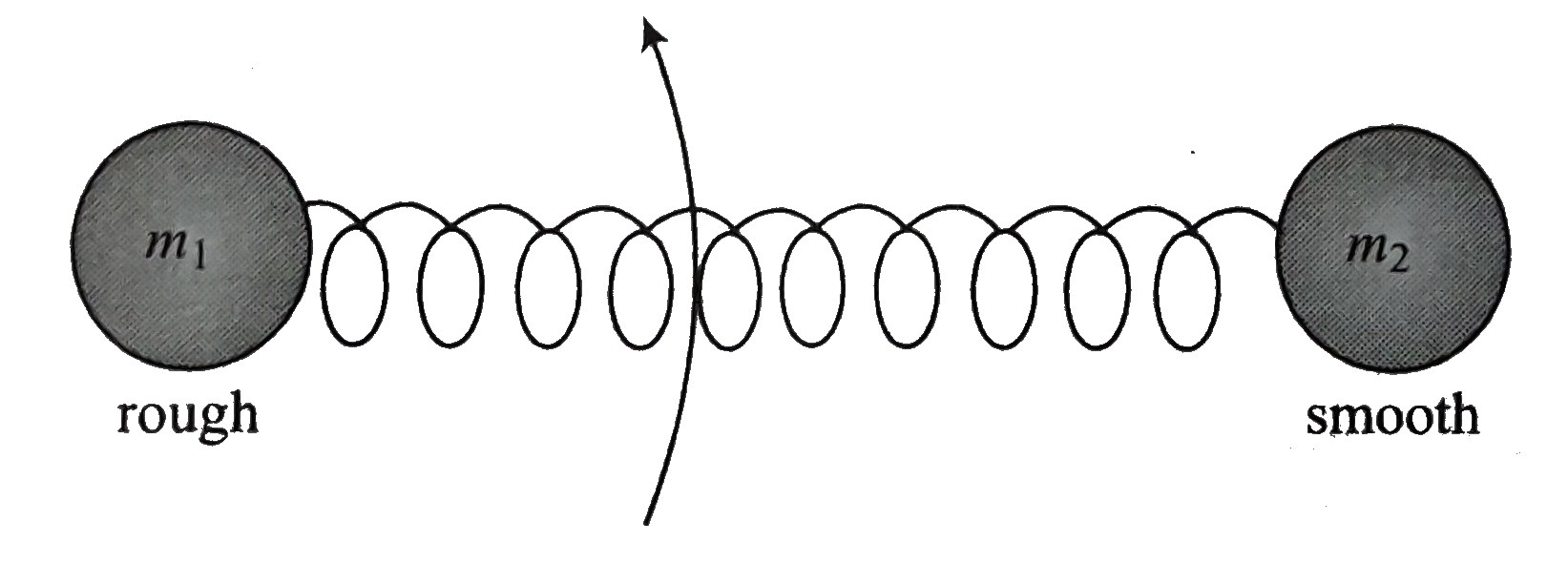
View SolutionA block of mass m1 connected with another of mass m2 by a light spring of natural length l0 and stiiffness k is kept stationary on a rough horizontal surface . The coefficient of friction between m1 and surface is μ and the block m2 is smooth .The block m2 is moved with certain the block m1 in horizontal plane Find the (a) maximum to m1 and (b) acceleration of m2 in part(a)
View SolutionTwo blocks of masses m_(1) and m_(2) are connected by an ideal sprit, of force constant k . The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m_(1) . Initially spring is relaxed, both the blocks are at rest. What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m_(1) and m_(2) are connected by an ideal sprit, of force constant k . The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m_(1) . Initially spring is relaxed, both the blocks are at rest. What is maximum elongation of spring.
View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is

View SolutionTwo blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :

View SolutionThe blocks ov mass m1kg and m2=2kg are connected by an ideal spring, rest on a rough horizontal surface. The spring is unstressed. The spring constant of spring is K=2N/m. The coefficient of friction between blocks and horizontal surface is μ=12. Now the left block is imparted a velocity u towards right as shown. The largest value of u( in m/s) such that the block of mass m2 never moves is ( Take g=10m/s2)
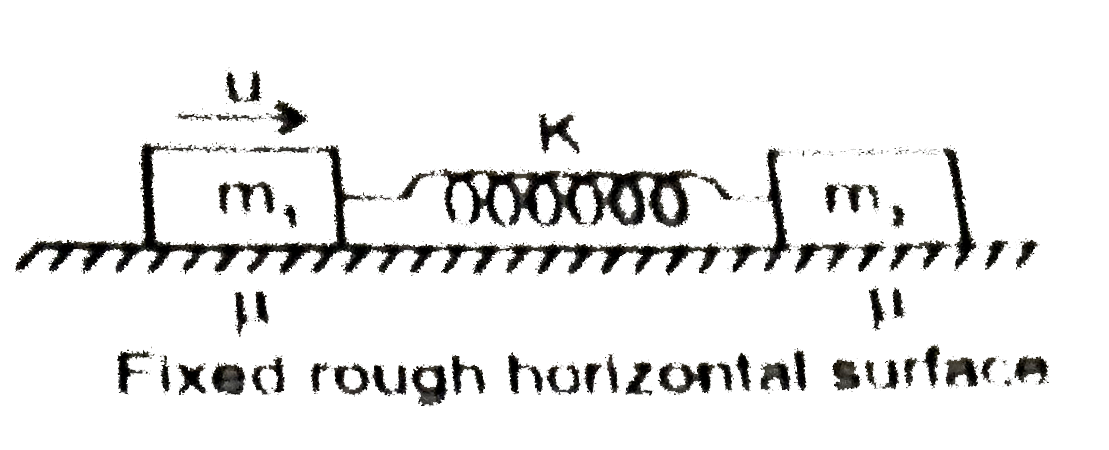
View SolutionTwo blocks of masses m_(1) and m_(2) are kept on a smooth horizontal table as shown in figure. Block of mass m_(1) (but not m_(2) is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m_(1) after the system is released is
View SolutionTwo blocks of masses m_(1) =1kg and m_(2) = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m_(1) is imparted an initial velocity v_(0) = 12cm/s to the right. The amplitude of osciallation is
View Solutionm द्रव्यमान का एक गुटका v चाल से क्षैतिज खुरदुरी सतह पर गतिमान है तथा चित्रानुसार स्प्रिंग नियतांक k वाली क्षैतिज रूप से व्यवस्थित स्प्रिंग से टकराता है। गुटके एवं फर्श के मध्य का घर्षण गुणांकμ है। स्प्रिंग का अधिकतम संपीड़न होगा-

View SolutionTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
View SolutionTwo blocks m_(1) and m_(2) of 1 kg and 2 kg are connected by a spring of spring constant K on a rough horizontal surface of coefficient of friction 0.4. A horizontal force F is applid on m_(1) so that it could just move block mass m_(2) . The value of F
View Solution
