A stone is thrown horizontally with a velocity of 10m/sec. Find the radius of curvature of it’s trajectory at the end of 3s after motion began. (g=10m/s2)
10√10m
100√10m
√10m
100m
The correct Answer is:B
To find the radius of curvature of the trajectory of a stone thrown horizontally with a velocity of 10 m/s after 3 seconds, we can follow these steps:
Step 1: Determine the vertical velocity (Vy) after 3 seconds
The vertical velocity can be calculated using the equation of motion:
Vy=u+at
Where:
- u=0 (initial vertical velocity)
- a=g=10m/s2 (acceleration due to gravity)
- t=3s
Substituting the values:
Vy=0+(10m/s2)(3s)=30m/s
Step 2: Determine the horizontal velocity (Vx)
Since the stone is thrown horizontally, the horizontal velocity remains constant:
Vx=10m/s
Step 3: Calculate the resultant velocity (Vt)
The resultant velocity Vt can be calculated using the Pythagorean theorem:
Vt=√Vx2+Vy2
Substituting the values:
Vt=√(10m/s)2+(30m/s)2=√100+900=√1000=10√10m/s
Step 4: Determine the normal acceleration (An)
The only acceleration acting on the stone is due to gravity, which acts vertically downward. The normal component of acceleration An can be calculated as:
An=g⋅cos(θ)
Where θ is the angle of the resultant velocity with respect to the horizontal. We can find cos(θ) using:
cos(θ)=VxVt=1010√10=1√10
Thus,
An=g⋅cos(θ)=10⋅1√10=10√10=√10m/s2
Step 5: Calculate the radius of curvature (R)
The radius of curvature R can be calculated using the formula:
R=Vt2An
Substituting the values we have:
R=(10√10)2√10=1000√10=100√10m
Final Answer
The radius of curvature of the stone's trajectory at the end of 3 seconds is:
R=100√10m
The vertical velocity can be calculated using the equation of motion:
Vy=u+at
Where:
- u=0 (initial vertical velocity)
- a=g=10m/s2 (acceleration due to gravity)
- t=3s
Vy=0+(10m/s2)(3s)=30m/s
Since the stone is thrown horizontally, the horizontal velocity remains constant:
Vx=10m/s
The resultant velocity Vt can be calculated using the Pythagorean theorem:
Vt=√Vx2+Vy2
Substituting the values:
Vt=√(10m/s)2+(30m/s)2=√100+900=√1000=10√10m/s
The only acceleration acting on the stone is due to gravity, which acts vertically downward. The normal component of acceleration An can be calculated as:
An=g⋅cos(θ)
Where θ is the angle of the resultant velocity with respect to the horizontal. We can find cos(θ) using:
cos(θ)=VxVt=1010√10=1√10
Thus,
An=g⋅cos(θ)=10⋅1√10=10√10=√10m/s2
The radius of curvature R can be calculated using the formula:
R=Vt2An
Substituting the values we have:
R=(10√10)2√10=1000√10=100√10m
The radius of curvature of the stone's trajectory at the end of 3 seconds is:
R=100√10m
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 427videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 4311videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 405videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A ball is thrown from the top of a 60m high tower with velocity 20√2m/s at 45∘ elevation.Find the radius of curvature of path at highest point. (g=10m/s2)
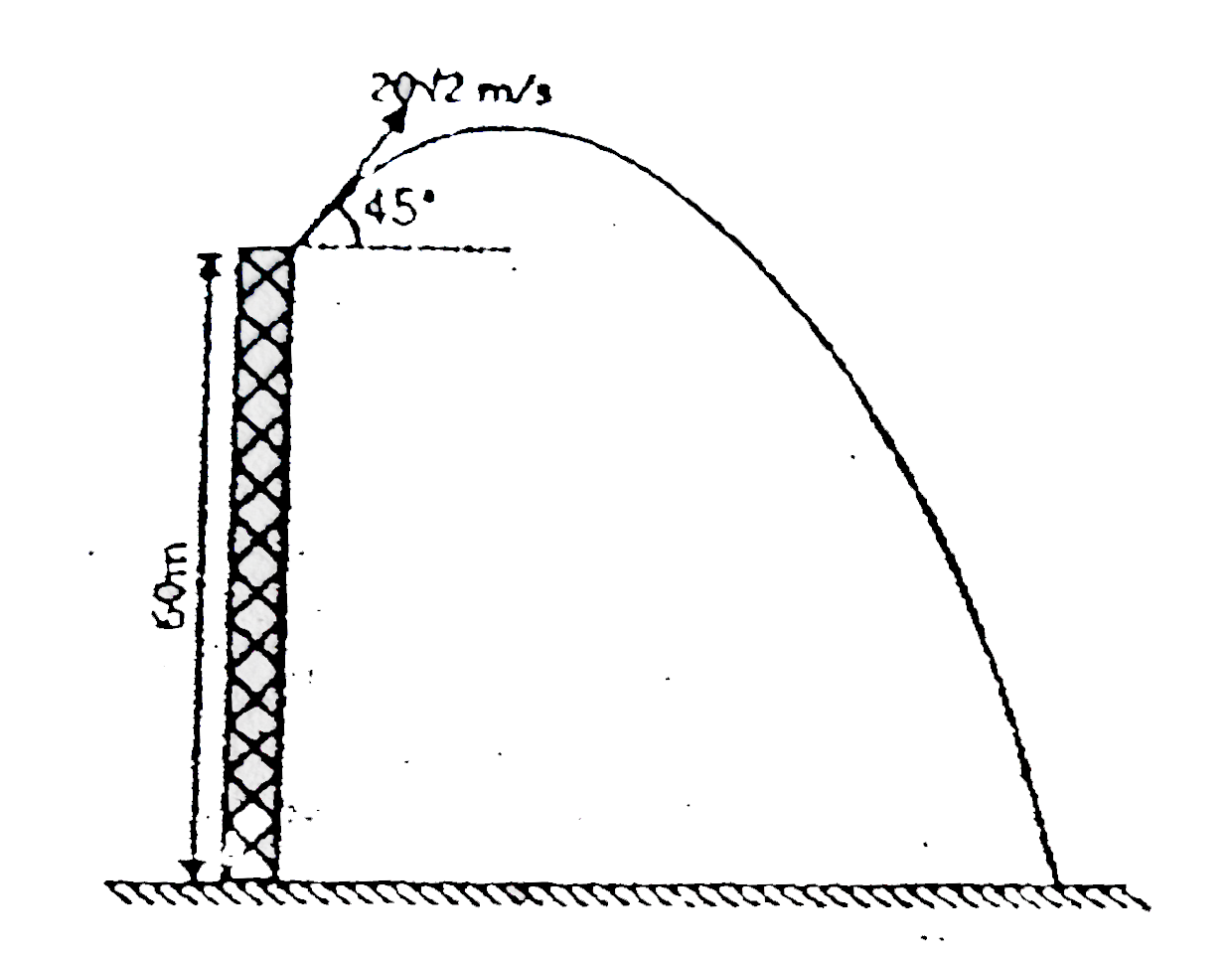View SolutionFrom the top of a tower, a particle is thrown vertically downwards with a velocity of 10m/s. The ratio of the distances, covered by it in the 3rd and 2nd seconds of the motion is (Takeg=10m/s2).
View Solution
Knowledge Check
- Question 1 - Select One
A stone is thrown horizontally with velocity u. The velocity of the stone 0.5 s later is 3u/2. The value of u is
A2.2ms−1B3.3ms−1C4.4ms−1D1.1ms−1
A heavy particle is projected from a point on the horizontal at an angle 60∘ with the horizontal with a speed of 10m/s. Then the radius of the curvature of its path at the instant of crossing the same horizontal is ……………………...
View SolutionA heavy particle is projected from a point on the horizontal at an angle 60∘ with the horizontal with a speed of 10m/s. Then the radius of the curvature of its path at the instant of crossing the same horizontal is ……………………...
View SolutionA particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s , find tangential and normal acceleration of the particle. Also, find radius of curvature of the trajectory at that point. (Take g=10m/s2)
View SolutionA stone is thrown horizontally with the velocity vx=15m/s. Determine the normal and tangential accelerations of the stone in I second after begins to move.
View SolutionA stone of mass 500g is dropped from the top of a tower of 100m height. Simultaneously another stone of mass 1 kg is thrown horizontally with a speed of 10ms−1 from same point. The height of the centre of mass of the above two stone system after 3 sec is (g=10ms−2)
View SolutionA ballon moves up with a velocity 5m/s. A stone is thrown from it with a horizontal velocity 2m/s relative to it. The stone hits the ground at a point 10m horizontally away from it. (Take g=10m/s2)
View SolutionA body is projected horizontally from the top of a tower with a velocity of 30 m/s. The velocity of the body 4 seconds after projection is (g = 10ms−2)
View Solution