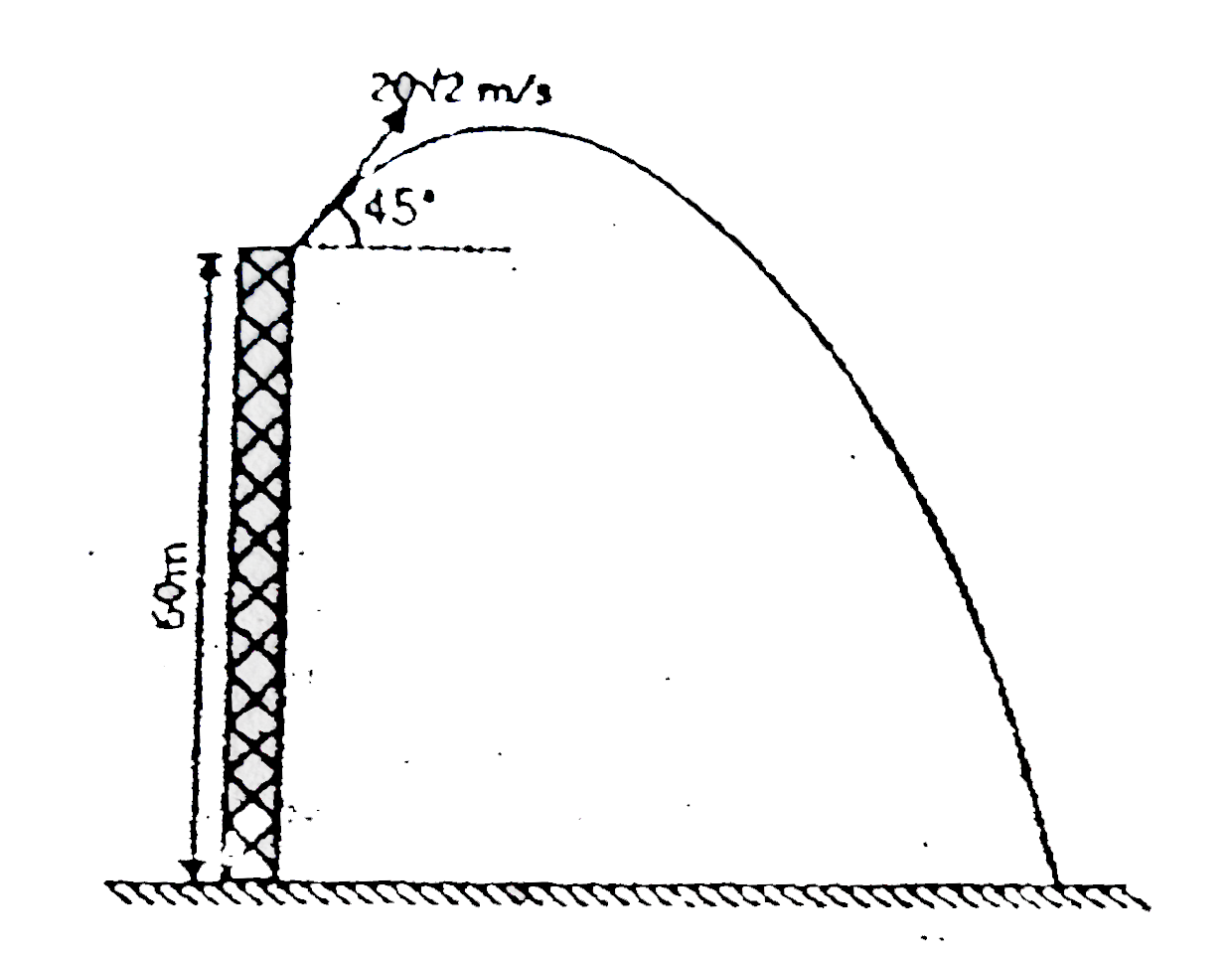
A ball is thrown from the top of a $60 m$ high tower with velocity $20 \sqrt{2} m / s$ at $45^{\circ}$ elevation.Find the radius of curvature of path at highest point. ( $g = 10 m / s^{2}$ )

A

$10 m$

B

$20 m$

C

$40 m$

D

$200 m$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$R = \frac{v^{2}}{a_{c}} = \frac{(u {cos 45}^{\circ})}{g} = \frac{{(20)}^{2}}{10} = 40 m$

|

Updated on:21/07/2023

Class 12 PHYSICS TEST PAPER

Topper's Solved these Questions

Similar Questions

The particle of mass 1 kg is projected with velocity $20 \sqrt{2}$ m/s at $45^{\circ}$ with ground . When , the particle is at highest point $(g = 10 m / s^{2})$ ,

View Solution
A ball is thrown from the top of $36 m$ high tower with velocity $5 m / s s$ at an angle $37^{\circ}$ above the horizontal as shown. Its horizontal distance on the ground is closest to [ $g = 10 m / s^{2}$
$:$
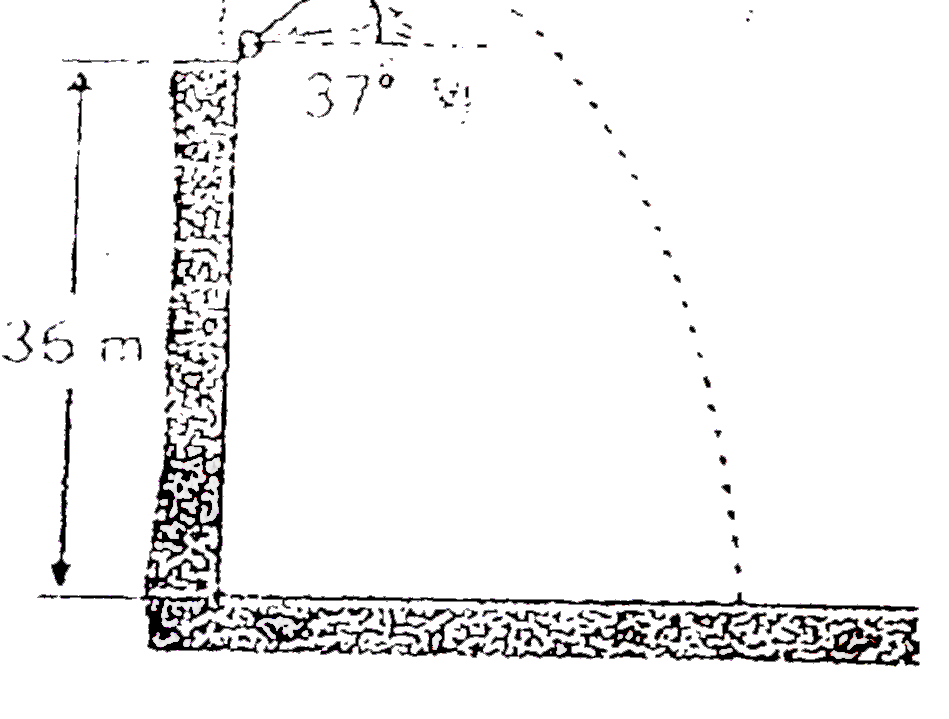View Solution

Knowledge Check

Question 1 - Select One
A ball is thrown from the top of a tower with an initial velocity of $10 m / s$ at an angle of $30^{\circ}$ above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower $(g = 10 m / s^{2})$ will be
A5 m
B20 m
C15 m
D10 m

ALLEN-TEST PAPER-Exercise (Physics)

Home
Ask Doubt
Profile