A particle begins to move with a tangential acceleration of constant magnitude 0.6m/s2 in a circular path . If it slips when total acceleration becomes 1m/s2, then the angle through which it would have turned before it stars to slip is :
1/3rad
2/3rad
4/3rad
2rad
The correct Answer is:B
To solve the problem, we need to determine the angle through which a particle would have turned before it starts to slip when moving in a circular path with a given tangential acceleration and a condition for slipping based on total acceleration.
1. Identify Given Data:
- Tangential acceleration, At=0.6m/s2
- Total acceleration at which slipping occurs, Anet=1m/s2
2. Understand the Relationship Between Accelerations:
The total acceleration Anet is the vector sum of the tangential acceleration At and the centripetal acceleration Ac:
Anet=√A2t+A2c
3. Express Centripetal Acceleration:
The centripetal acceleration Ac can be expressed in terms of angular velocity ω and radius r:
Ac=v2r=ω2r
where v is the linear velocity of the particle.
4. Relate Angular Velocity to Tangential Acceleration:
The tangential acceleration is related to the angular acceleration α by:
At=rα
Since the particle starts from rest, we can use the kinematic equation:
ω2=ω20+2αθ
where ω0=0 (initial angular velocity).
5. Substituting Values:
Since ω0=0:
ω2=2αθ
And since α=Atr=0.6r:
ω2=2(0.6r)θ
6. Substituting into Total Acceleration Equation:
Now substituting Ac into the total acceleration equation:
1=√(0.6)2+(0.6⋅2θr)2
This simplifies to:
1=√0.36+(1.2θr)2
7. Squaring Both Sides:
Squaring both sides gives:
1=0.36+1.44θ2r2
Rearranging this gives:
0.64=1.44θ2r2
8. Solving for θ:
Rearranging for θ2:
θ2=0.64r21.44=64144r2=49r2
Taking the square root:
θ=23r
9. Final Result:
The angle through which the particle would have turned before it starts to slip is:
θ=23radians
Conclusion:
Thus, the angle through which the particle turns before slipping is 23 radians.
- Tangential acceleration, At=0.6m/s2
- Total acceleration at which slipping occurs, Anet=1m/s2
The total acceleration Anet is the vector sum of the tangential acceleration At and the centripetal acceleration Ac:
Anet=√A2t+A2c
The centripetal acceleration Ac can be expressed in terms of angular velocity ω and radius r:
Ac=v2r=ω2r
where v is the linear velocity of the particle.
The tangential acceleration is related to the angular acceleration α by:
At=rα
Since the particle starts from rest, we can use the kinematic equation:
ω2=ω20+2αθ
where ω0=0 (initial angular velocity).
Since ω0=0:
ω2=2αθ
And since α=Atr=0.6r:
ω2=2(0.6r)θ
Now substituting Ac into the total acceleration equation:
1=√(0.6)2+(0.6⋅2θr)2
This simplifies to:
1=√0.36+(1.2θr)2
Squaring both sides gives:
1=0.36+1.44θ2r2
Rearranging this gives:
0.64=1.44θ2r2
Rearranging for θ2:
θ2=0.64r21.44=64144r2=49r2
Taking the square root:
θ=23r
The angle through which the particle would have turned before it starts to slip is:
θ=23radians
Thus, the angle through which the particle turns before slipping is 23 radians.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 427videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 4311videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 405videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionA particle starts moving from rest at t=0 with a tangential acceleration of constant magnitude of πm/s2 along a circle of radius 6 m. The value of average acceleration, average velocity and average speed during the first 2√3 s of motion, are respectively :
View SolutionA particle is moving with a constant angular acceleration of 4rad/s2 in a circular path. At time t=0 , particle was at rest. Find the time at which the magnitudes of centripetal acceleration and tangential acceleration are equal.
View SolutionIf acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
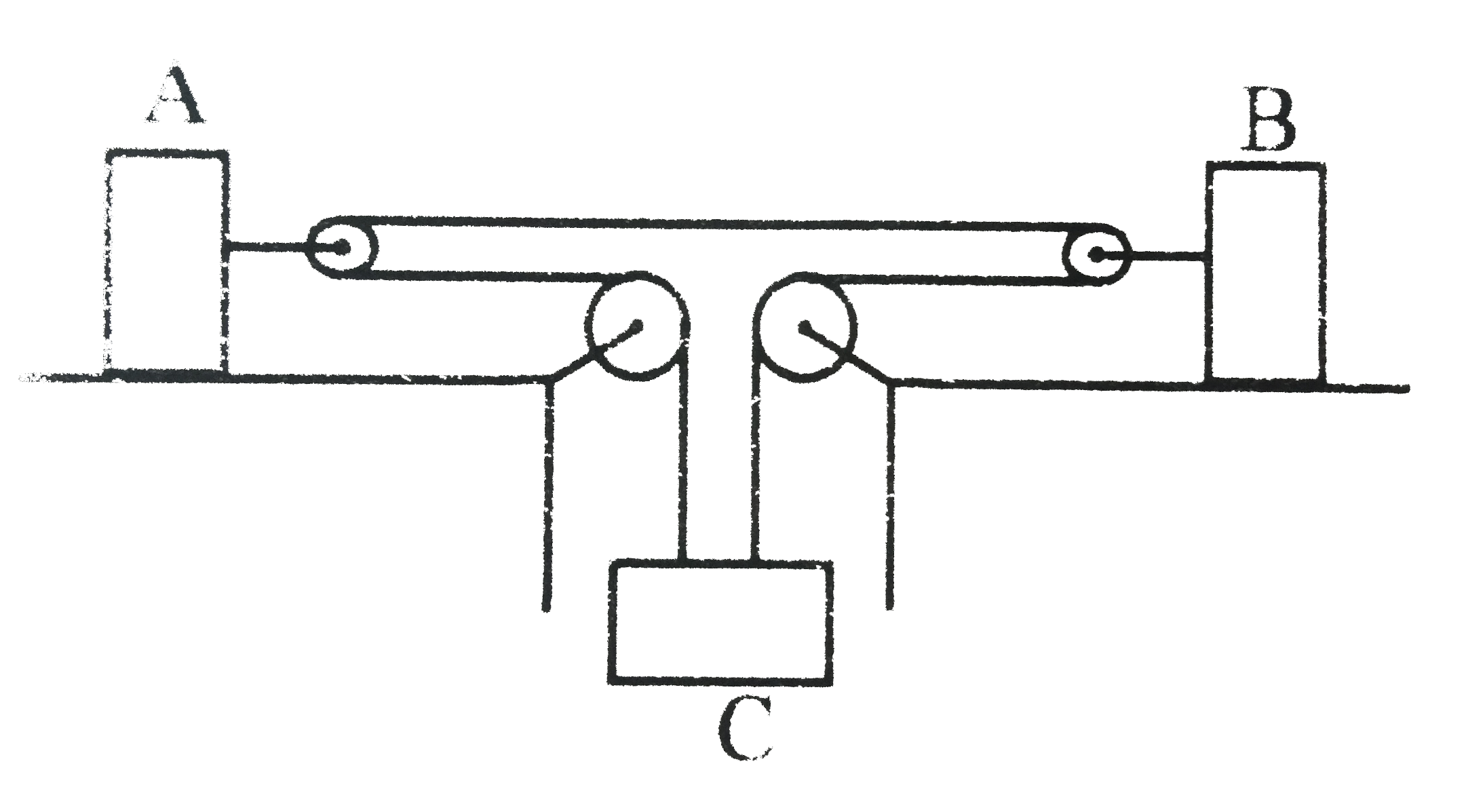 View Solution
View SolutionFind the total acceleration of a particle, moving in a circular track of radius 2 m, with constant angular acceleration of 1 rad/sec2 at time t = 2 seconds from the center
View SolutionIf acceleration of block B is 4m/s2 upward & that of C is 6m/s2 downward. Find acceleration of A :−
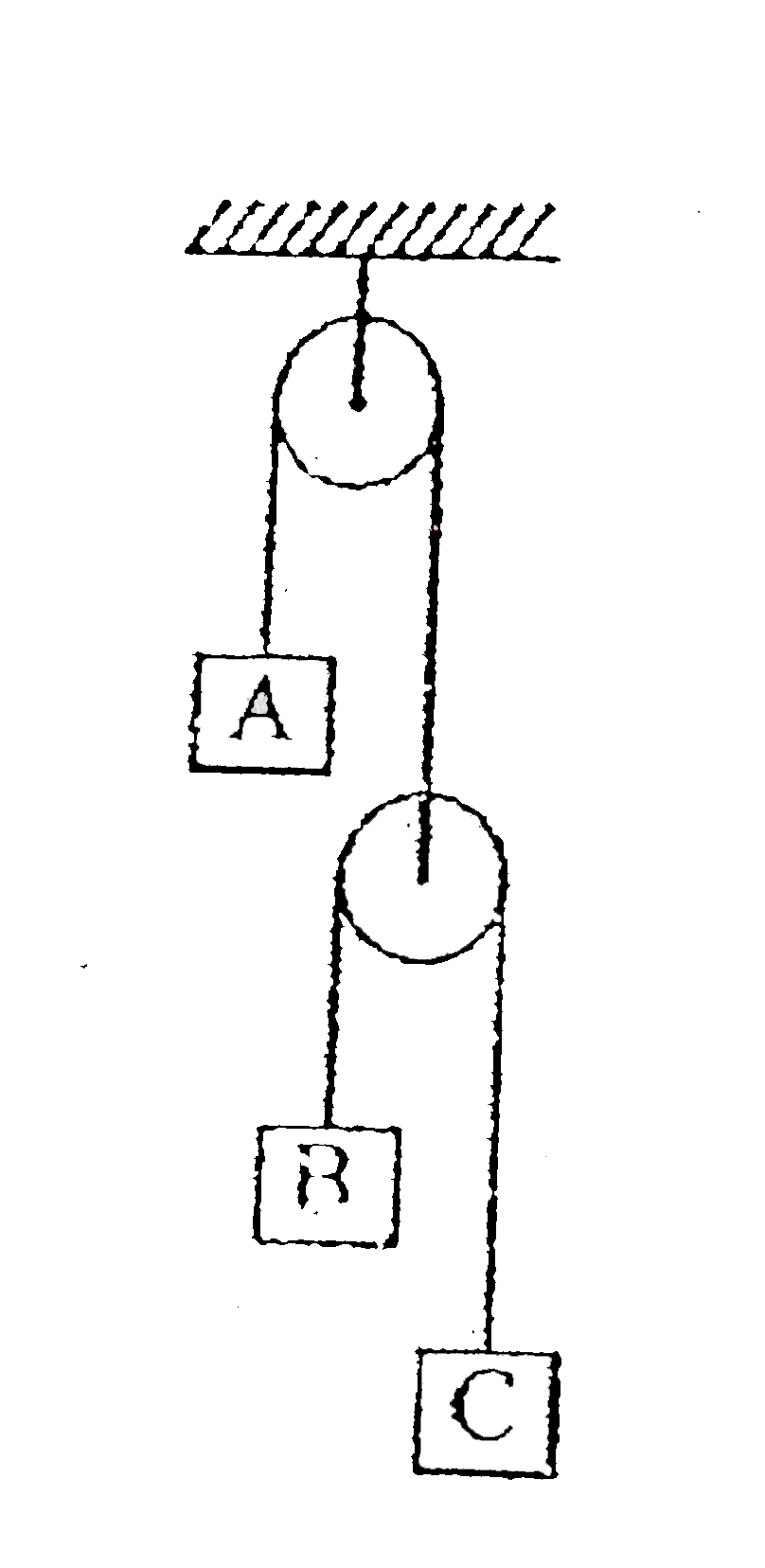 View Solution
View SolutionA particle moves in a circle with constant tangential acceleration starting from rest. At t = 1/2 s radial acceleration has a value 25% of tangential acceleration. The value of tangential acceleration will be correctly represented by
View SolutionTwo particles P and Q are moving on circle. At a certain instant of time both the particles and diametrically opposite and P has tangential acceleration 8m/s2 and centripetal acceleration 5m/s2 whereas Q has only e centripetal acceleration of1m/s2. At that instant acceleration (inm/s2) of P with respect to Q is
View SolutionA cyclist is moving with a constant acceleration of 1.2 m/s2 on a straight track. A racer is moving on a circular path of radius 150 m at constant speed of 15 m/s. Find the magnitude of velocity of racer which is measured by the cyclist has reached a speed of 20 m/s for the position represented in the figure -
 View Solution
View Solution

