A small hoop of mass m is given an initial velocity of magnitude v0 on the horizontal circular ring of radius 'r'. If the coefficient of kinetic friction is μk the tangential acceleration of the hoop immediately after is release is ( assume the horizontal ring to be fixed and not in contact with any supporting surface )
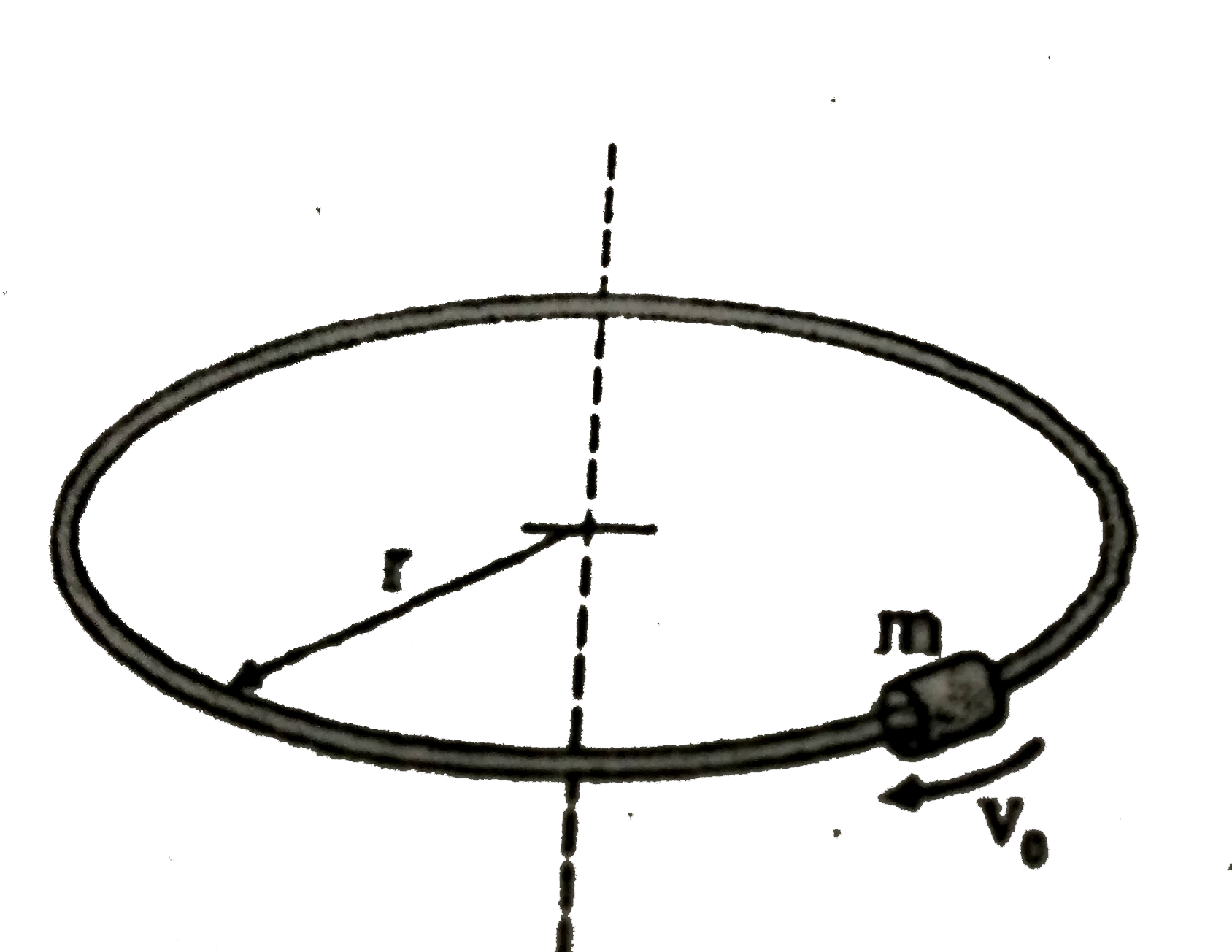
μkg
μkv20r
μk√g2+v2r
μk√g2+v0r2
The correct Answer is:D
The free body diagram of hoop is
∴The normal reaction N=√m2g2+m2v40r2
∴ Frictional force =μkN=μk√m2g2+m2v40r2
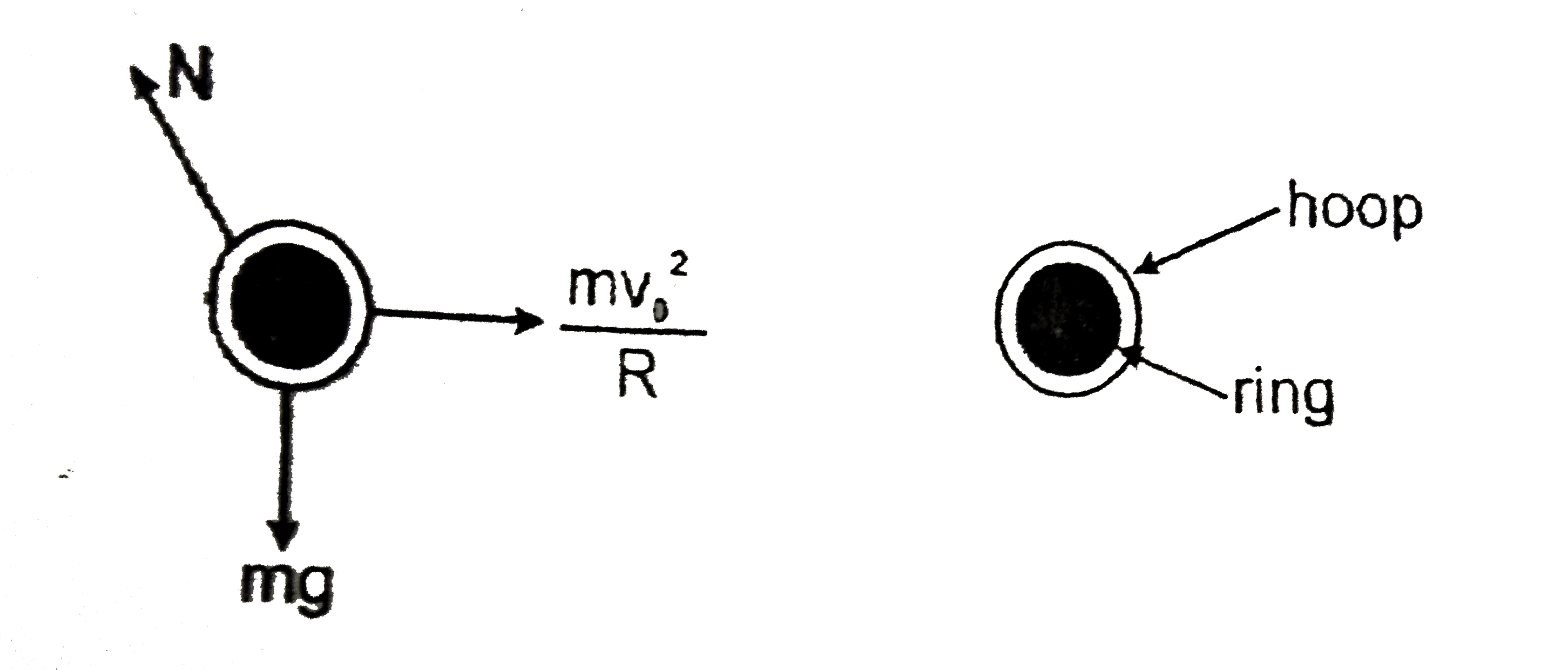
∴ tangentail acceleration =μkNm
=μk√g2+v40r2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 52
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 53
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 50
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Choose the correct option:
A small collar of mass m is given an initial velocity of magnitude v0 on the horizontal circular track fabricated from a slender rod. If the coefficient of kinetic friction is μK, determine the distance traveled before the collar comes to rest. (Recognize that the friction force depends on the net normal force).

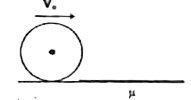
View SolutionA ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
View Solution
Knowledge Check
A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
AωoμkR2gBωog2μkRC2ωoRμkgDωoR2μkg
A block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0+ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.

View SolutionA hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA car starts rest, on a horizontal circular road of radius R, the tangential acceleration of the car is a. The friction coefficient between the road and the tyre is μ Find the speed at which car will skid and also find the distance after travelling it skids.
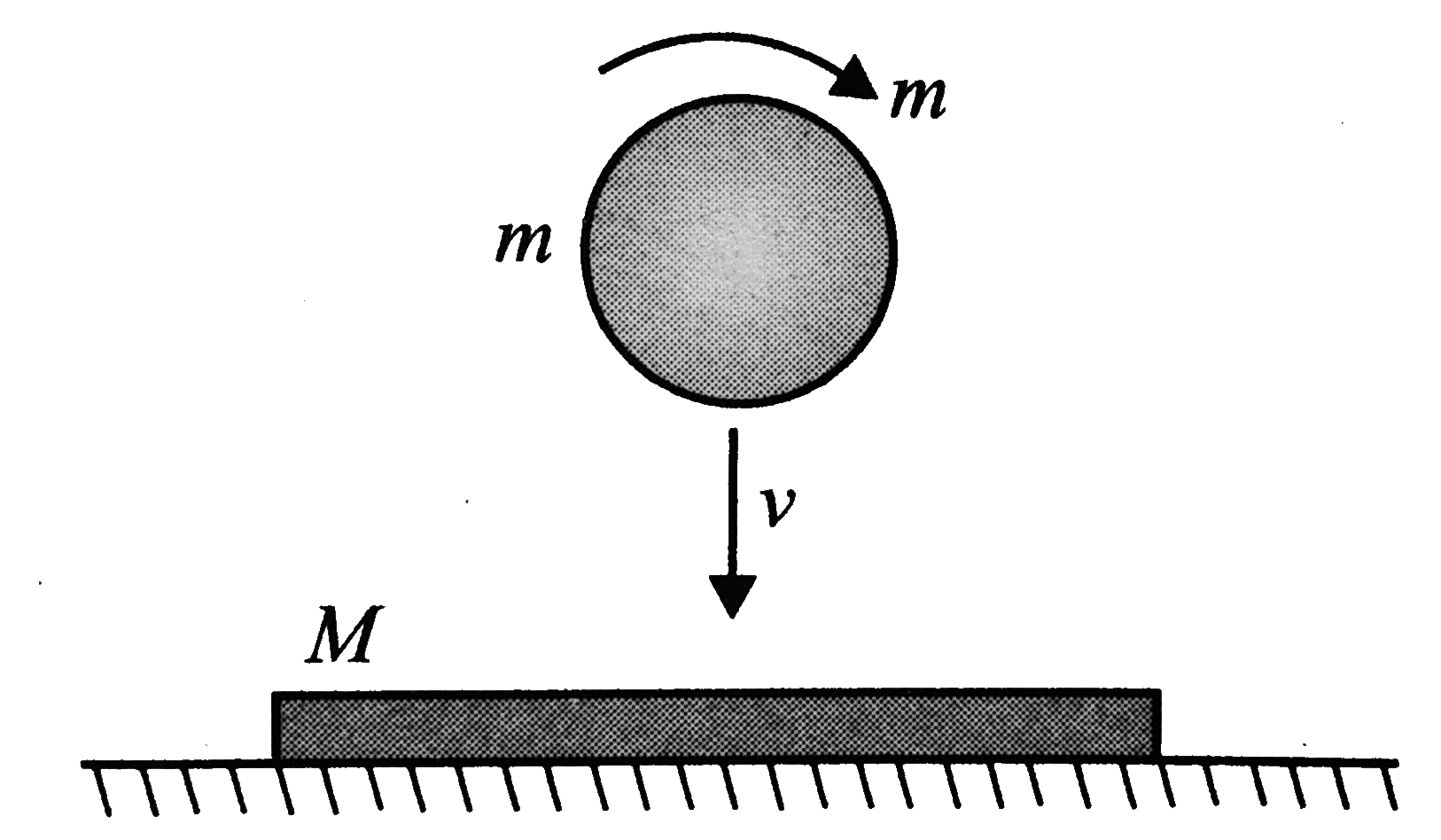
View SolutionA solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity of the sphere in horizontal direction immediately after the impact (given: Rω=5).
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View Solution
