A block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0+ax. Find the kinetic energy of the block as function of x before it comes to rest.
To find the kinetic energy of a block of mass m moving with an initial velocity v0 on a rough horizontal surface where the coefficient of friction varies with position, we can follow these steps:
Step 1: Identify the Forces Acting on the Block
The forces acting on the block include:
- The gravitational force W=mg acting downward.
- The normal force N acting upward.
- The frictional force Ff acting opposite to the direction of motion.
Step 2: Express the Frictional Force
The coefficient of friction is given by:
μ=μ0+ax
Thus, the frictional force can be expressed as:
Ff=μN=(μ0+ax)mg
Step 3: Calculate the Work Done by the Frictional Force
The work done by the frictional force as the block moves from x=0 to x is:
W=−∫x0Ffdx=−∫x0(μ0+ax)mgdx
Step 4: Perform the Integration
Calculating the integral:
W=−mg(μ0x+ax22)x0=−mg(μ0x+ax22)
Step 5: Apply the Work-Energy Theorem
According to the work-energy theorem:
W=ΔK=Kf−Ki
where Ki=12mv20 and Kf=12mv2. Thus:
−mg(μ0x+ax22)=12mv2−12mv20
Step 6: Rearranging the Equation
Rearranging the equation gives:
12mv2=12mv20−mg(μ0x+ax22)
Step 7: Express Kinetic Energy as a Function of x
Multiplying through by 2 and simplifying:
mv2=mv20−2mg(μ0x+ax22)
K=12mv2=12mv20−mg(μ0x+ax22)
Final Expression for Kinetic Energy
Thus, the kinetic energy K as a function of x is:
K(x)=12mv20−mg(μ0x+ax22)
---
The forces acting on the block include:
- The gravitational force W=mg acting downward.
- The normal force N acting upward.
- The frictional force Ff acting opposite to the direction of motion.
The coefficient of friction is given by:
μ=μ0+ax
Thus, the frictional force can be expressed as:
Ff=μN=(μ0+ax)mg
The work done by the frictional force as the block moves from x=0 to x is:
W=−∫x0Ffdx=−∫x0(μ0+ax)mgdx
Calculating the integral:
W=−mg(μ0x+ax22)x0=−mg(μ0x+ax22)
According to the work-energy theorem:
W=ΔK=Kf−Ki
where Ki=12mv20 and Kf=12mv2. Thus:
−mg(μ0x+ax22)=12mv2−12mv20
Rearranging the equation gives:
12mv2=12mv20−mg(μ0x+ax22)
Multiplying through by 2 and simplifying:
mv2=mv20−2mg(μ0x+ax22)
K=12mv2=12mv20−mg(μ0x+ax22)
Thus, the kinetic energy K as a function of x is:
K(x)=12mv20−mg(μ0x+ax22)
Similar Questions
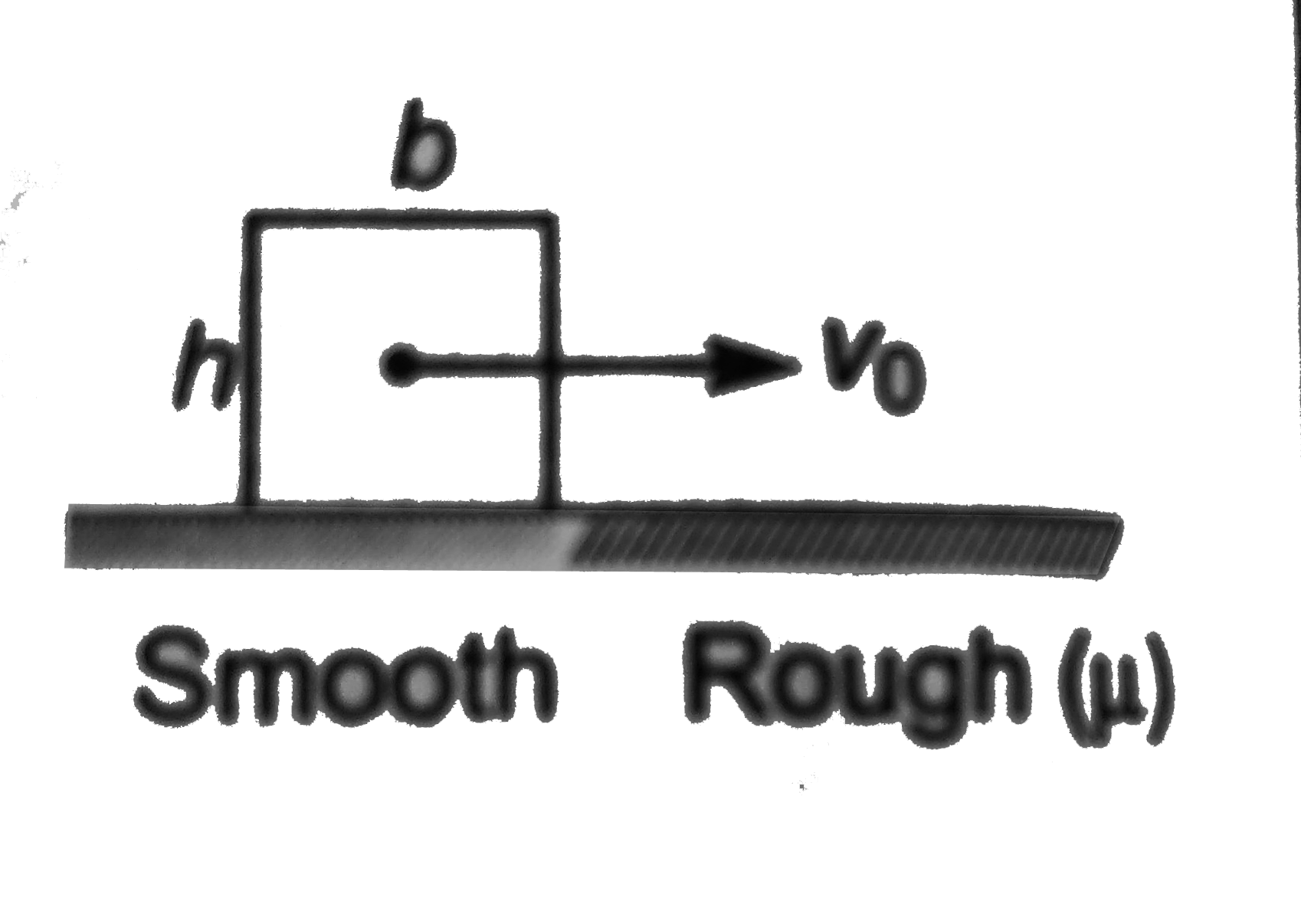
A rectangular block of size (×h) moving with velocity v0 enters on a rough surface where the coefficient of friction is μ as shown in figure. Identify the correct statement.
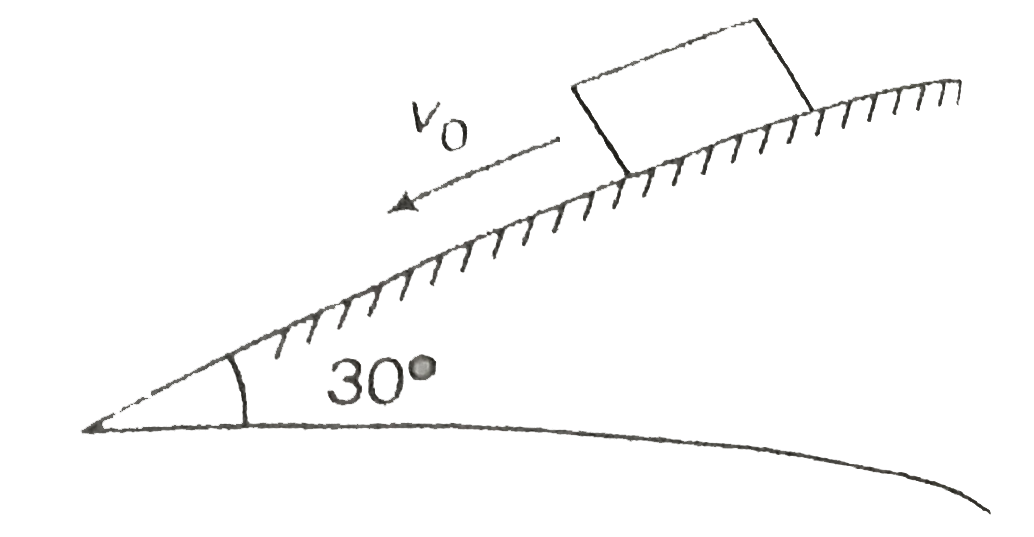
View SolutionA block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will
View Solution
Knowledge Check
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
A10ms−2B5ms−2C15ms−2D0.5ms−2
A block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .

View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
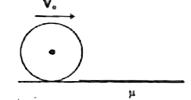
View SolutionA ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA small body of mass m moving with velocity v0 on rough horizontal surface, finally stops due to friction. Find, the mean power developed by the friction force during the motion of the body, if the frictional coefficient μ=0.27,m=1 kg and v0=1.5ms−1.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
View Solution
