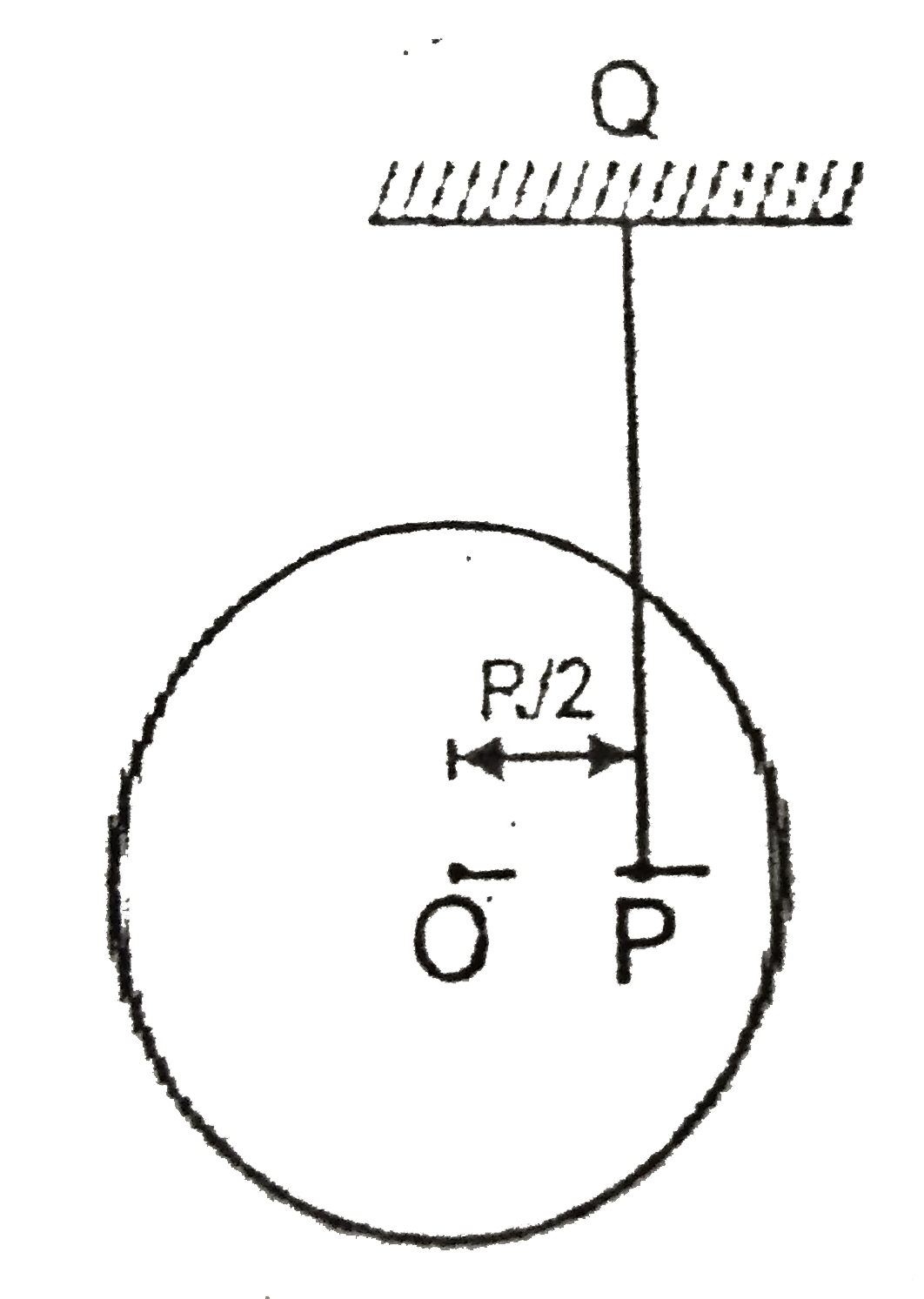
A uniform disc of mass M and radius R is released from the shown position . PQ is s tring , OP is a horizontal line , O is the centre of the disc and distance OP is R/2. The tension in the string just after the disc is released will be :
Mg2
Mg3
2Mg3
none of these
The correct Answer is:C
(C)
Applying Newton's law on the centre of mass O
Mg−T=ma{a= acceleration of centre of mass }
τ=Iα, about centre of mass
T=R2=MR22.α
Also a=R2α from above equations T=2mg3

Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 664videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 672videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 645videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),
 View Solution
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
 View Solution
View SolutionGiven a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
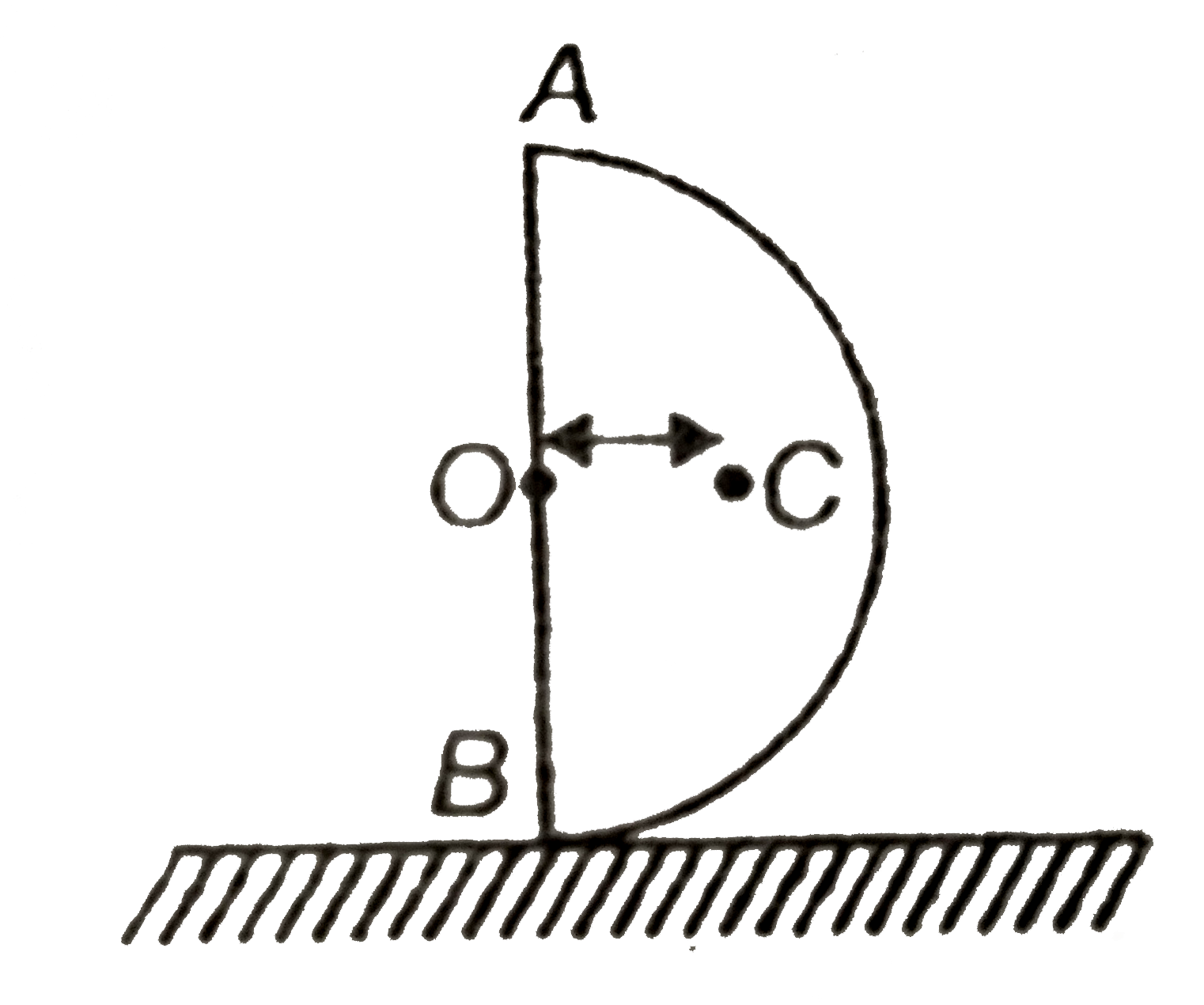
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is
 View Solution
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionA uniform disc of mas M and radius R is smoothly pivoted at O. A light iextensible string wrapped over the disc hangs a particle of mass m. If the system is released from rest, assuming that the string does not slide on the disc, find the angular speed of the disc as the function of time using impulse momentum equation.
 View Solution
View SolutionA particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
View Solution

