A student throws a horizontal stick of length L up into the air. At the moment it leaves her hand the speed of stick's closes end is zero. The stick completes N turns as it is caought by the student at the initial release point. Find the height h to which the centre of mass of the rod rises.
The correct Answer is:πNL4
To solve the problem of finding the height h to which the center of mass of a horizontal stick of length L rises when thrown into the air, we can follow these steps:
Step 1: Understanding the Problem
The stick is thrown horizontally, and at the moment of release, the speed of the stick's closest end is zero. The stick completes N turns before being caught back at the release point. The center of mass of the stick is located at a distance of L2 from the point of release.
Step 2: Relating Angular Velocity and Linear Velocity
The linear velocity vcm of the center of mass of the stick can be related to its angular velocity ω by the formula:
vcm=ω⋅r
where r is the distance from the pivot (the release point) to the center of mass. Here, r=L2, so:
vcm=ω⋅L2
Step 3: Finding the Time of Flight
The stick completes N revolutions before being caught. The time period T for one complete revolution is given by:
T=2πω
Thus, the total time t for N revolutions is:
t=N⋅T=N⋅2πω
Step 4: Relating Time of Flight to Motion
The stick is thrown horizontally and falls under the influence of gravity. The time of flight can also be expressed in terms of the vertical motion:
t=2vcmg
Equating the two expressions for t:
2vcmg=N⋅2πω
This simplifies to:
vcm=Nπgω
Step 5: Finding the Height
The height h to which the center of mass rises can be calculated using the equation of motion for projectile motion:
h=v2cm2g
Substituting the expression for vcm:
h=12g(Nπgω)2
This simplifies to:
h=N2π2g2g2ω2
Thus, we can express h as:
h=N2π22gω2
Step 6: Final Expression for Height
Using the earlier relation ω2L=2πNg, we can substitute ω2 in our height equation:
h=N2π2L4g
Conclusion
The height h to which the center of mass of the rod rises is given by:
h=NπL4
The stick is thrown horizontally, and at the moment of release, the speed of the stick's closest end is zero. The stick completes N turns before being caught back at the release point. The center of mass of the stick is located at a distance of L2 from the point of release.
The linear velocity vcm of the center of mass of the stick can be related to its angular velocity ω by the formula:
vcm=ω⋅r
where r is the distance from the pivot (the release point) to the center of mass. Here, r=L2, so:
vcm=ω⋅L2
The stick completes N revolutions before being caught. The time period T for one complete revolution is given by:
T=2πω
Thus, the total time t for N revolutions is:
t=N⋅T=N⋅2πω
The stick is thrown horizontally and falls under the influence of gravity. The time of flight can also be expressed in terms of the vertical motion:
t=2vcmg
Equating the two expressions for t:
2vcmg=N⋅2πω
This simplifies to:
vcm=Nπgω
The height h to which the center of mass rises can be calculated using the equation of motion for projectile motion:
h=v2cm2g
Substituting the expression for vcm:
h=12g(Nπgω)2
This simplifies to:
h=N2π2g2g2ω2
Thus, we can express h as:
h=N2π22gω2
Using the earlier relation ω2L=2πNg, we can substitute ω2 in our height equation:
h=N2π2L4g
The height h to which the center of mass of the rod rises is given by:
h=NπL4
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 687videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 695videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 664videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.View SolutionA student throws soft balls out of the window at different angles to the horizontal. All soft balls have the same initial speed v=10√3ms−1. It turns out that all soft balls landing velocities make angles 30∘ or greater with the horizontal. Find the height h (in m) of the window above the ground.
View SolutionA student throws soft balls out of the window at different angles to the horizontal. All soft balls have the same initial speed v=10√3ms−1. It turns out that all soft balls landing velocities make angles 30∘ or greater with the horizontal. Find the height h (in m) of the window above the ground.
View SolutionA mass m = 50 g is dropped on a vertical spring of spring constant 500 N/m from a height h= 10 cm as shown in figure (18-E14). The mass sticks to the spring and executes simple harmonic oscillations after that. A concave mirror of focal length 12 cm facing the mass is fixed with its principal axis coinciding with the line of motion of the mass, its pole being at a distance of 30 cm from the free end of the spring. Find the length in which the image of the mass oscillates.
View SolutionThe rod of length l and mass m lies on a smooth floor. A ball of mass m moving horizotally with a speed u0 striked one end of rod and stick to it. After the collision, the point on the rod that moves translationally ( without any rotation) in the previous direction of motion of the ball.

A. Is the centre of C of the rod.
B. Is the left end A of the rod.
C. Lies at a distance l/4 to the left of point C
D. Lies at a distance l/4 to the right of point C.View SolutionA uniform rod of mass m and length L is hinged at one of its end with the ceiling and another end of the rod is attached with a thread which is attached with the horizontal ceiling at point P. If one end of the rod is slightly displaced horizontally and perpendicular to the rod and released. If the time period of small oscillation is 2π√2lsinθxg . Find x.
 View Solution
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView Solution
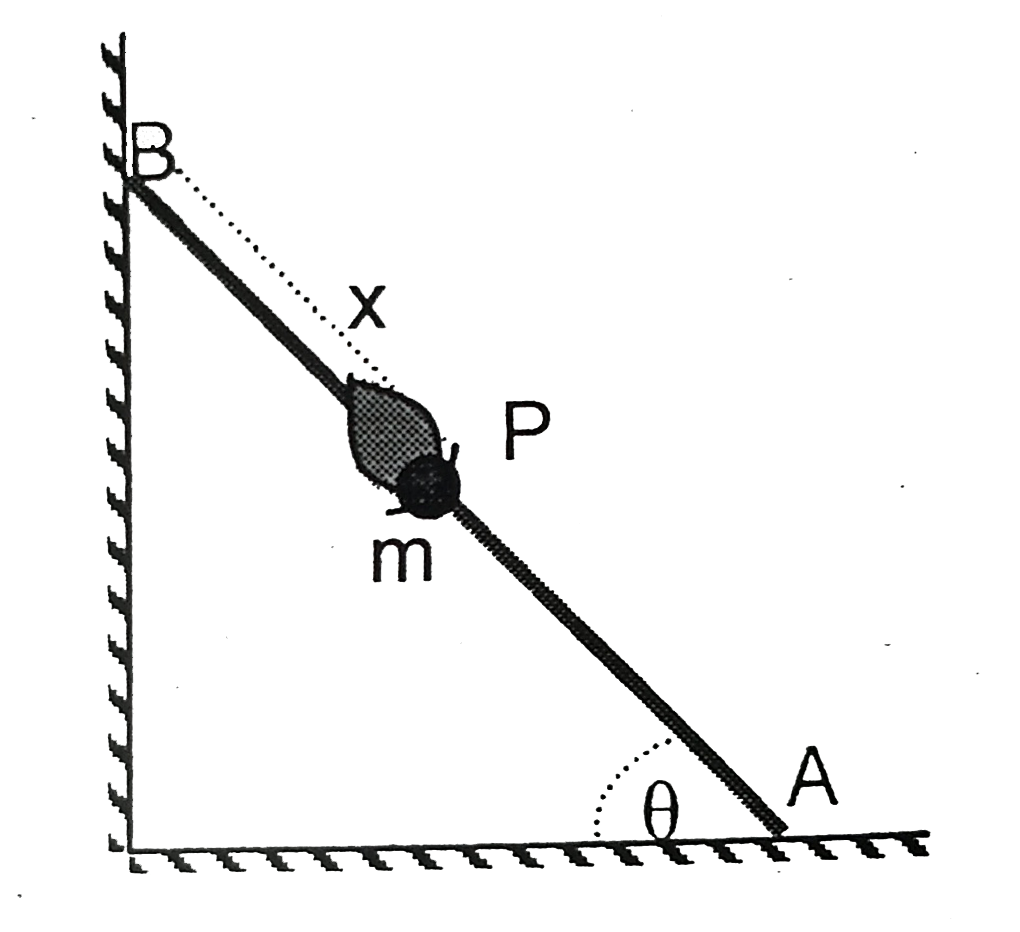
A thin, uniform rod of mass M and length L is at rest on a smooth horizontal surface. A particle of same mass M collides with the rod at one end perpendicular to its length with velocity V∘ and sticks to it. C is the middle point of the rod and D is a point at a distance of L/4 from end A. the time taken by the rod turn through 90∘ after collisions.View SolutionA light stick of length l rests with its one end against the smooth wall and other end against the smooth horizontal floor as shown in the figure. The bug starts at rest from point B and moves such that the stick always remains at rest. aP is the magnitude of acceleration of but of mass m, which depends upon its distance of x from the top end of the stick. Choose the correct option (s)
 View Solution
View Solution
