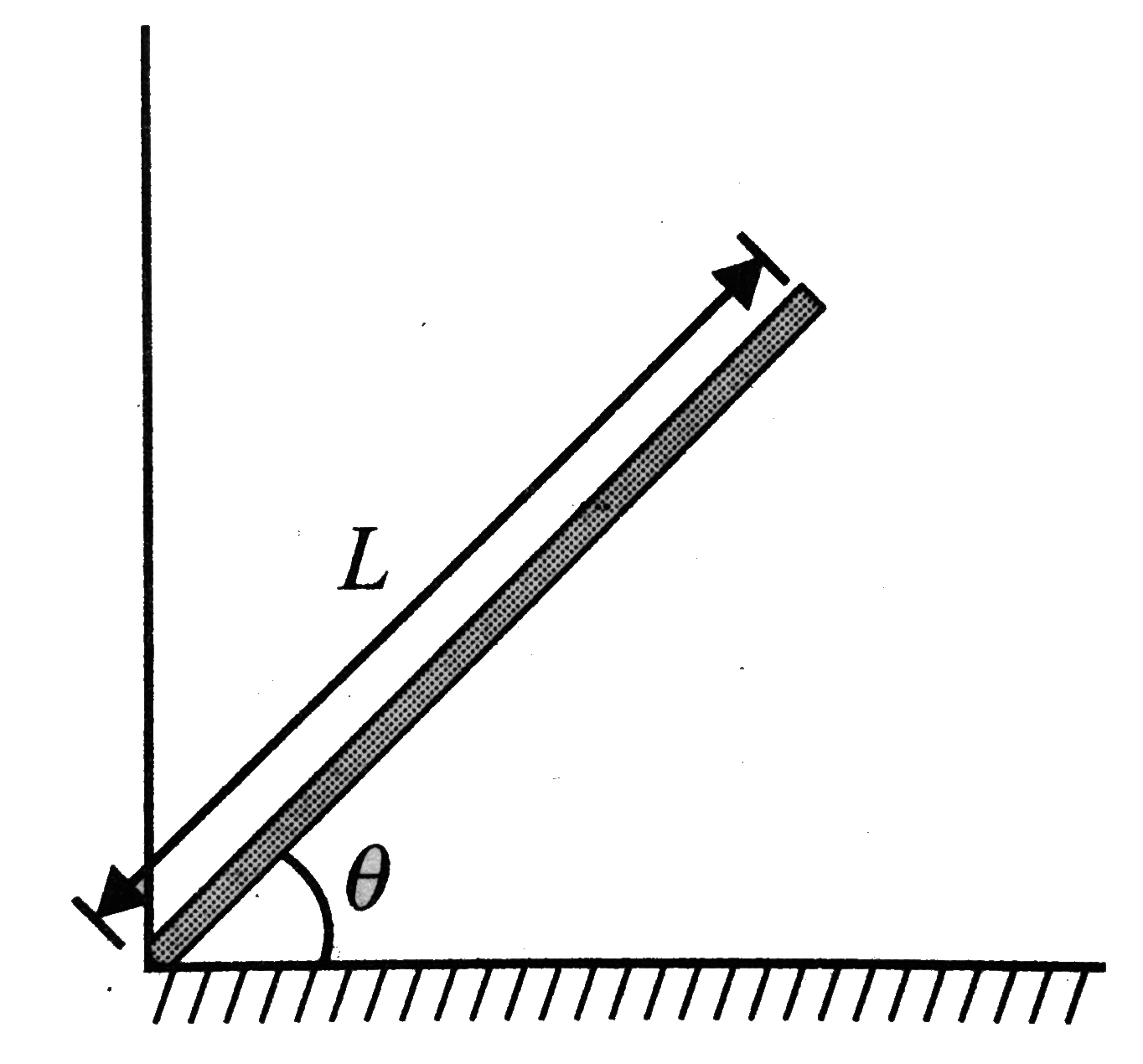
A uniform pole of length L and mass M is pivoted on the ground with a frictionless hinge. The pole makes an angle θ with the horizontal. The moment of inertia of the pole about one end is (13)ML2. If it starts falling front the position shown in the accompanying figure, the linear acceleration of the free end of the pole immediately after release would be
23gcosθ
23g
g
32gcosθ
The correct Answer is:D
About point O
Torque τ=Iα
Mg(L2cosθ)=ML23α⇒3g2Lcosθ=α
Initially centripetal acceleration of point P is zero
(∵ac=v2r=0r=0)
Acceleration of point P is √a2C+a2t
=at=Lα=32gcosθ
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 69
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:comprehension
Explore 127 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 67
Explore 2 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
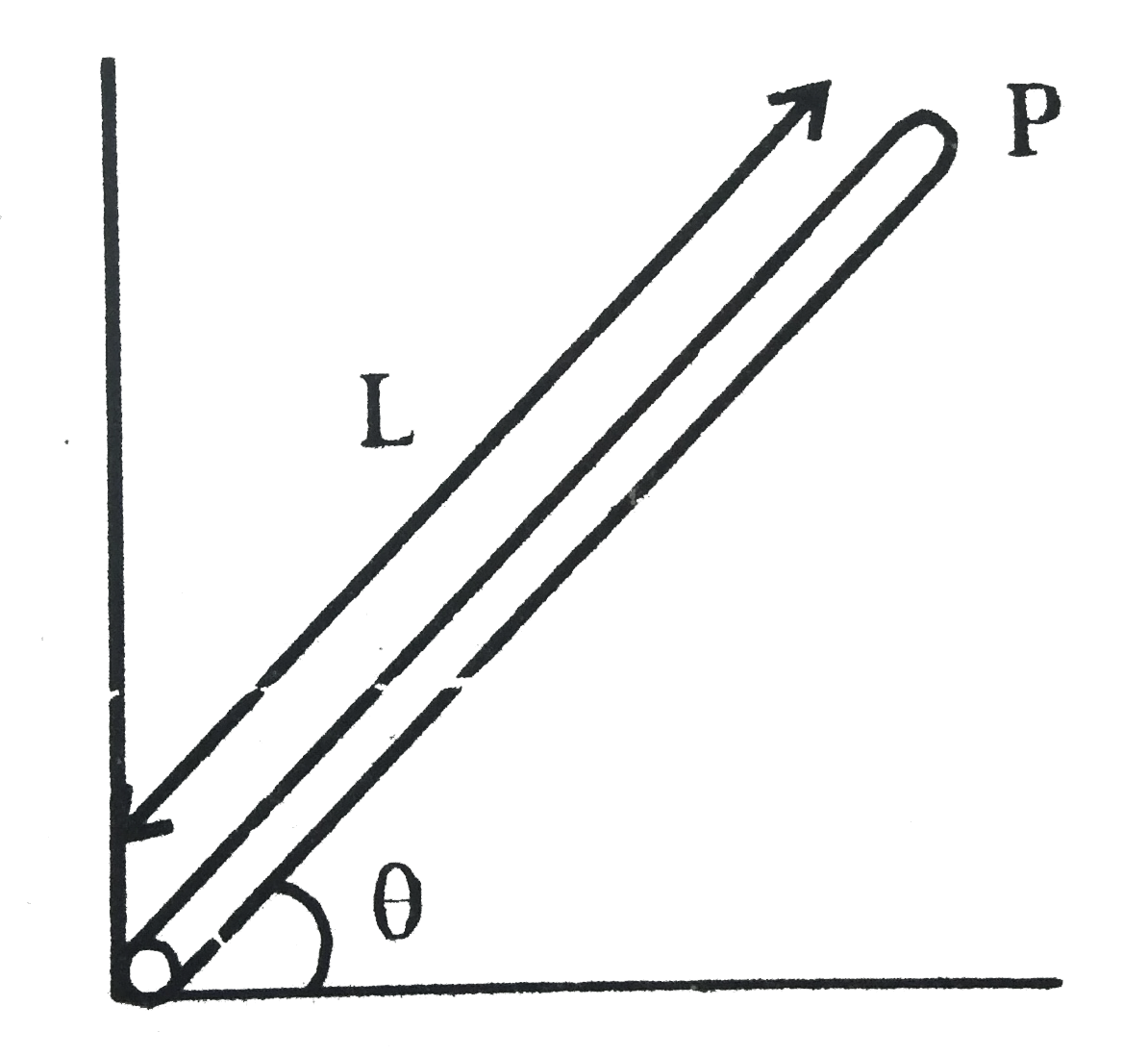
A uniform flag pole of length Land mass M in pivoted on the ground with a frictionless hinge. The flag pole makes an angle θ with the horizontal. The moment of inertia of the flag pole about one end is (1/3)ML2. If starts falling from the position shown in figure, the linear acceleration of the free end of the flag pole-labeled P - would be.
 .
.
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be

View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
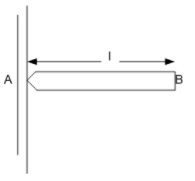
View SolutionA uniform rod AB of length l and mass m is free to rotate about an Axis passing through A and perpendicular to length of the rod. The rod is released from rest as shown in figure. Given that the moment of inertia of the rod about A is ml23 The initial angular acceleration of the rod will be
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at ann angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?
View SolutionA thin uniform bar of mass m and length 2L is held at an angle 30∘ with the horizontal by means of two vertical inextensible strings, at each end as shown in figure. If the string at the right end breaks, leaving the bar to swing, determine the tension in the string at the left end and the angular acceleration of the bar immediately after string breaks.

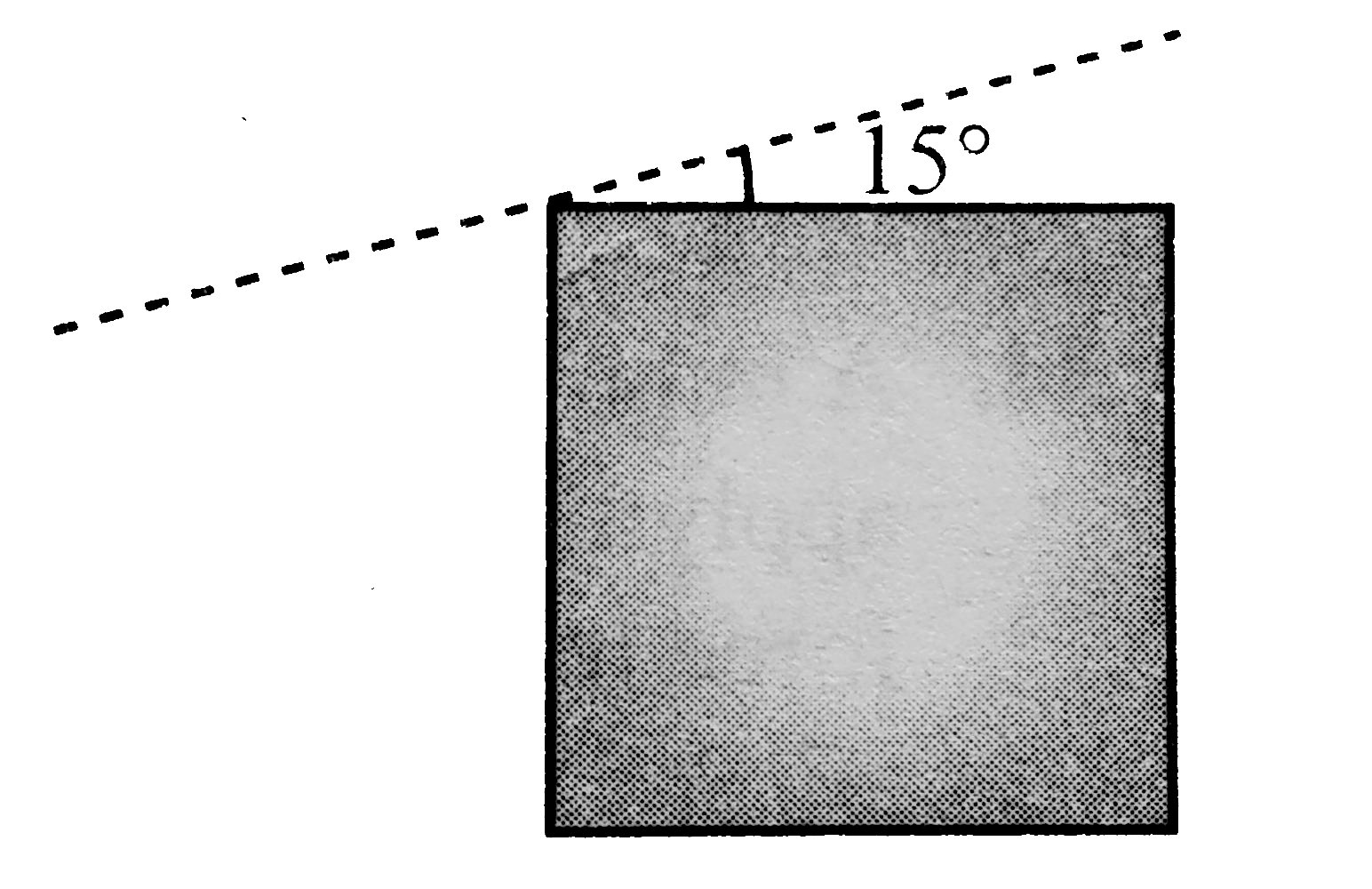
View SolutionA square plate of mass M and edge L is shown in the figure. The moment of inertia of the plate about the axis in the plane of plate and passing through one of its vertex making an angle 15∘ horizontal is
View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA non-uniform cylinder of mass m, length l and radius r is having its centre of mass at a distance l.4 from the centre and lying on the axis of the cylinder. The cylinder is kept in a liquid of uniform density ρ. The moment of inertia of the rod about the centre of mass is l. The angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is

View Solution