A particle of mass m1 is projected to the right with speed v1 onto a smooth wedge of mass m2 which is simulateoulsy projected due the left with a speed v2. If the particle attains the highest point of the wedge, find h.

Applying work energy theorem
Wtotal=△Kblocks,cm+△Kcm
As no external forces acting, the velocity of centre of mass will be constant. Hence △Kcm=0
Hence Wtotal=△Kblocks,cm
Wgravity=[12μv2rel]final−[12μv2rel]initial
−m1gh0−12(m1m2m1+m2)(v1+v2)2
−m1gh=−12(m1m2m1+m2)(v1+v2)2
h=12m2(v1+v2)2g(m1+m2)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
View SolutionA small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

View Solution
Knowledge Check
A particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
Amg=mv2rBmg>mv2rCmg≤mv2rDmg≥mv2rA particle of mass m is projected upword with velocity v=ve2 (ve) escape of the particle is
A−GMm2RB−GMm4RC−3GMm4RD−2GMm3R
A small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
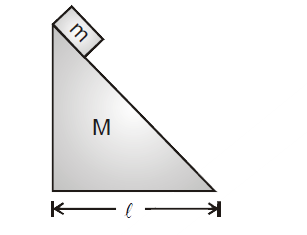
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :

View SolutionA particle of mass m is projected upword with velocity v=ve2 (ve) escape of the particle is
View Solution
