Two infinitely long rods carry equal linear denisty λ each. They are perpendicular to each other and they are in different planes and separated by a distance d. Find the electrostatic force on once rod due to the other
The correct Answer is:A, B, D
To find the electrostatic force on one infinitely long rod due to another infinitely long rod that is perpendicular to it and separated by a distance d, we can follow these steps:
Step 1: Understand the Configuration
We have two infinitely long rods, each carrying a linear charge density λ. One rod is placed along the y-axis (YZ plane), and the other rod is placed along the x-axis (YX plane). The distance between the two rods is d.
Step 2: Identify the Electric Field Due to One Rod
The electric field E due to an infinitely long charged rod at a distance r from it can be expressed as:
E=2kλr
where k is Coulomb's constant (k=14πϵ0).
Step 3: Calculate the Electric Field at the Location of the Other Rod
Since we want to find the force on the rod along the y-axis due to the rod along the x-axis, we will calculate the electric field at a distance d from the x-axis rod:
E=2kλd
Step 4: Calculate the Force on the Rod
The force F on a segment of the rod due to the electric field can be calculated using:
F=qE
where q is the charge on the segment of the rod. For a small length dx of the rod along the y-axis, the charge dq is given by:
dq=λdy
Thus, the force on this segment is:
dF=dq⋅E=λdy⋅2kλd
This simplifies to:
dF=2kλ2ddy
Step 5: Integrate to Find the Total Force
To find the total force F on the entire rod along the y-axis, we integrate dF over the entire length of the rod:
F=∫∞−∞dF=∫∞−∞2kλ2ddy
Since the rod is infinitely long, the integral diverges, but we can express the total force in terms of the linear charge density:
F=2kλ2d⋅L
where L is the length of the rod considered. For practical purposes, we can consider the force per unit length.
Step 6: Substitute k and Simplify
Substituting k=14πϵ0:
F=2⋅14πϵ0λ2d⋅L=λ22πϵ0d⋅L
Final Result
The electrostatic force per unit length on one rod due to the other is:
F=λ22πϵ0d
We have two infinitely long rods, each carrying a linear charge density λ. One rod is placed along the y-axis (YZ plane), and the other rod is placed along the x-axis (YX plane). The distance between the two rods is d.
The electric field E due to an infinitely long charged rod at a distance r from it can be expressed as:
E=2kλr
where k is Coulomb's constant (k=14πϵ0).
Since we want to find the force on the rod along the y-axis due to the rod along the x-axis, we will calculate the electric field at a distance d from the x-axis rod:
E=2kλd
The force F on a segment of the rod due to the electric field can be calculated using:
F=qE
where q is the charge on the segment of the rod. For a small length dx of the rod along the y-axis, the charge dq is given by:
dq=λdy
Thus, the force on this segment is:
dF=dq⋅E=λdy⋅2kλd
This simplifies to:
dF=2kλ2ddy
To find the total force F on the entire rod along the y-axis, we integrate dF over the entire length of the rod:
F=∫∞−∞dF=∫∞−∞2kλ2ddy
Since the rod is infinitely long, the integral diverges, but we can express the total force in terms of the linear charge density:
F=2kλ2d⋅L
where L is the length of the rod considered. For practical purposes, we can consider the force per unit length.
Substituting k=14πϵ0:
F=2⋅14πϵ0λ2d⋅L=λ22πϵ0d⋅L
The electrostatic force per unit length on one rod due to the other is:
F=λ22πϵ0d
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.31
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.32
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.29
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
In Q-2, if vectors are perpendicular to each other then find the value of λ.
View Solution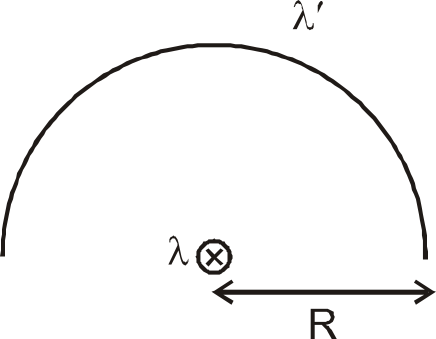
In the figure shown an infinitely long wire of uniform linear charge density λ is kept perpendicular to the plane of figure such that it extends upto infinity on both sides of the paper. Find the electrostatic force on a semicircular ring kept such that its geometrical axis coincides with the wire. The semicircular ring has a uniform linear charge density λ'.
View Solution
Knowledge Check
The nucleus of helium atom contains two protons that are separated by distance 3.0×10−15m. The magnitude of the electrostatic force that each proton exerts on the other is
A20.6 NB25.6 NC15.6 ND12.6 N
Two long wires, carrying currents i1andi2, are placed perpendicular to each other in such a way that they just avoid a contact. Find the magnetic force on a small length dl of the second wire situated at a distance l from the first wire. (figure)

View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
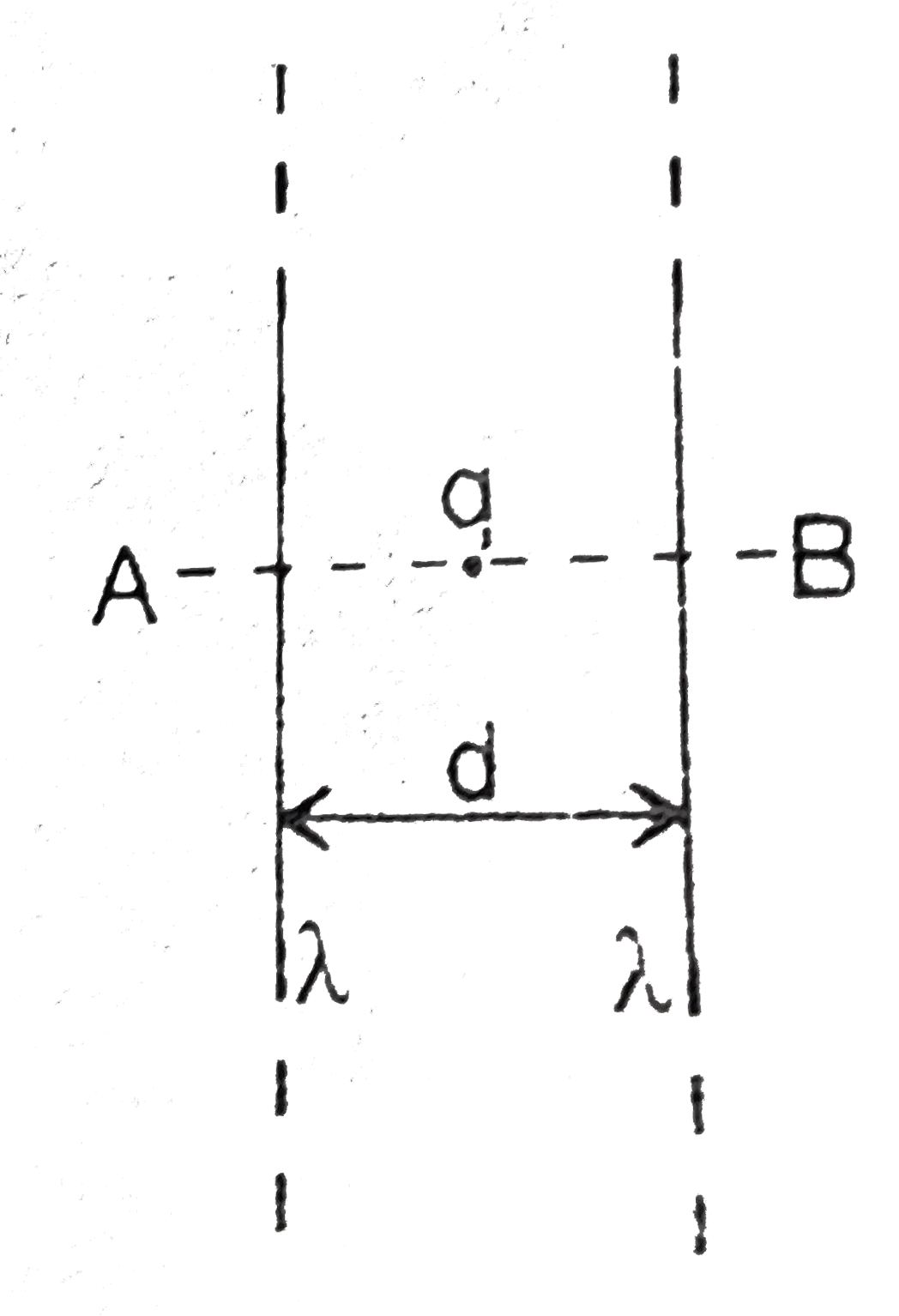
View SolutionTwo infinitely long thin straight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
View SolutionTwo identical conducting balls A and B have charges- Q and + 3Q respectively. They are brought in contact with each other and then separated by a distance d part. Find the nature of the Coulomb force between them.
View SolutionTwo infinitely long linear conductors are arranged perpendicular to each other and are in mutually perpendicular planes as shown in Fig. If I1=2A along the y-axis, I2=3A, along -ve z-axis and AP=AB=1cm, the value of magnetic field strength →B at P is

View SolutionTwo long wires, carrying currents i1andi2, are placed perpendicular to each other in such a way that they just avoid a contact. Find the magnetic force on a small length dl of the second wire situated at a distance l from the first wire. (figure)

View SolutionThe planes x=0 and y=0 (A) are parallel (B) are perpendicular to each other (C) interesect in z-axis (D) none of these
View Solution