Two point like charges Q1 and Q2 are positioned at point 1 and 2. The firld intensity to the right of the chaege Q2 on the line that passes through the two charges varies accoreing to a law that is represented schematically in fig. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l.
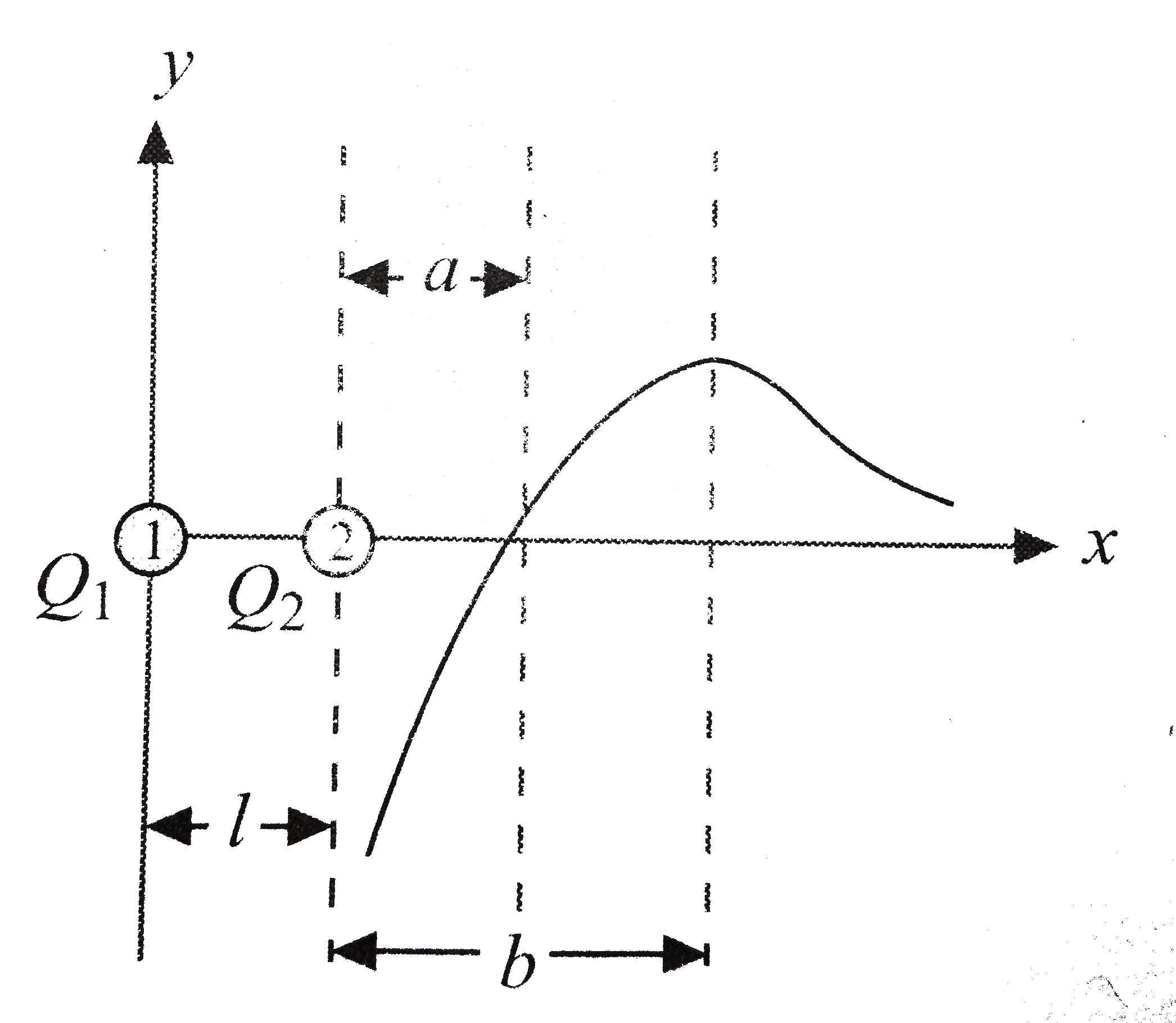
The ratio of the absolute values of the charges |Q1/Q2| is
Charge at point a is positive and charge at point b is negative
Charge at point a is negative and charge at point b is positive
Both charges are positive
Both charges are negative
The correct Answer is:A
∵ Electric field near point b is −∞
∴'b' shluld be negative electric field at x1 is O which possible only if 'a' and 'b' are of opposite sign
∴'a' is positive
Charge b is negative and charge a is positive

E at A=0(A=)E=2)
⇒|Qa|(l+x1)2=|Qb|(x1)2
∣∣∣QaQb∣∣∣=(l+x1x1)2=(1+lx1)2
W at a general X
K|Qa|(l+x2)−K|Qb|(x2)
=K|Qa|{1(l+x)2−∣∣∣QbQa∣∣∣1x2}
If E is a maximum, dEdx=0
⇒−2(l+x)3+(x1l+x1)22x3=0
(l+x)2=x3(l+x1x1)2
l+x=x(l+x1x1)23
x2=l(l+x1x1)23−1
x2=l(l+x1x1)23−1,∣∣∣QaQb∣∣∣=(1+lx1)2
Charge b is negative and charge a is positive.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.31
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.32
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.29
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Two point charge Qa and Qb are positional at point A and B. The field strength to the right of charge Qb on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is l=21cm.
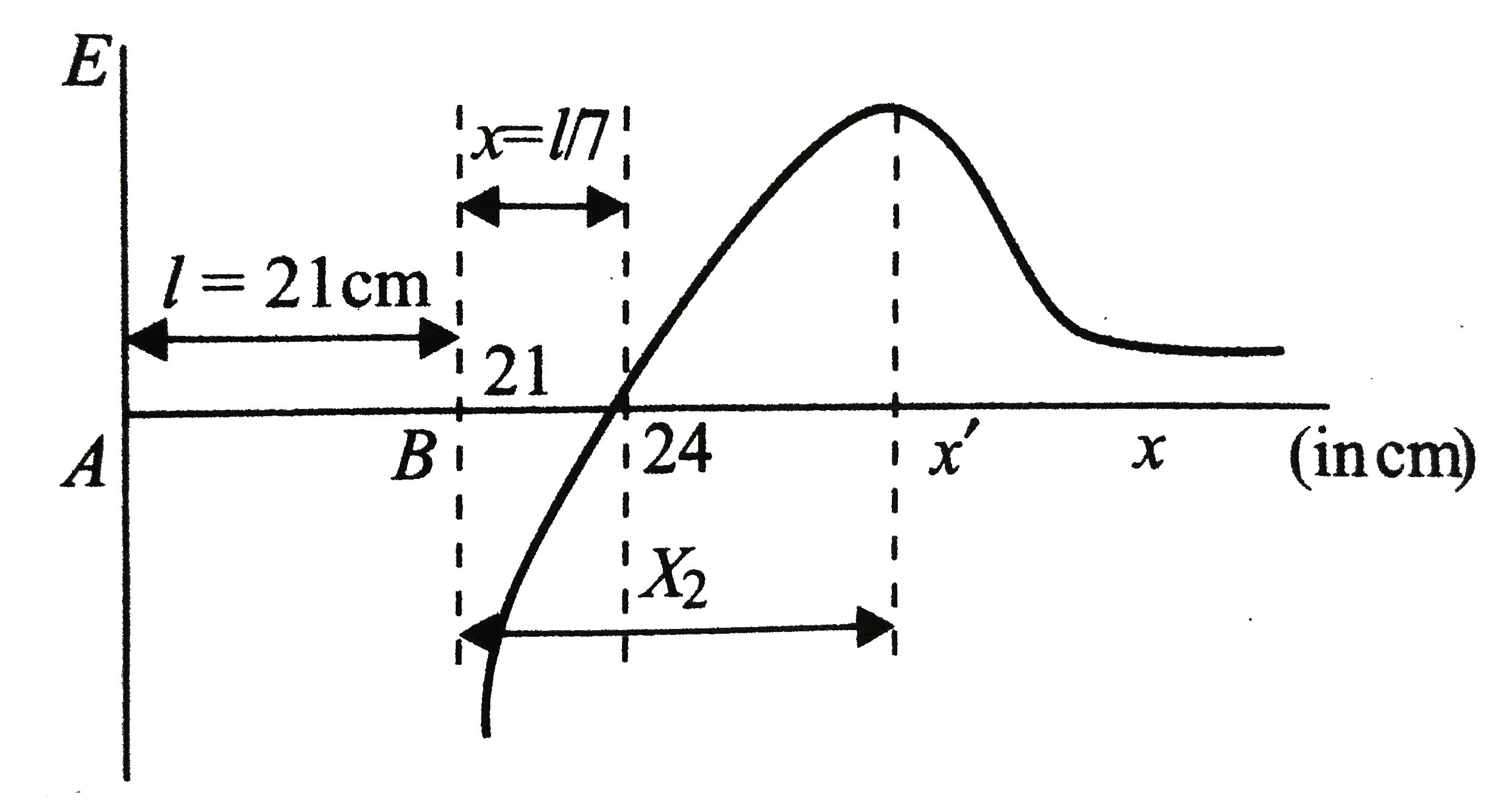
(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strength is maximum.
View SolutionTwo point charge Qa and Qb are positional at point A and B. The field strength to the right of charge Qb on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is l=21cm.

(a) Find the sign of the charges.
(b) Find the ratio between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strength is maximum.
View SolutionTwo point charges Q and -Q/4 are separated by a distance x.
View SolutionTwo point charges +Q and -Q are separated by a certain distance. The resultant electric field is parallel to the line joining the charges at the points
View SolutionA positive charge +q1 is located to the left of a negative charge −q2 On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity The first place is between the charges and is 4.00 cm to the left of the negative charge. The second place is 7.00cm to the right of the negative charge if q2=−12μC , what is the value of charge q1∈μC
View SolutionTwo point charges (+Q) and (−2Q) are fixed on the X-axis at positions a and 2a from origin respectively. At what positions on the axis, the resultant electric field is zero
View SolutionTwo point like charges q1 and q2 are fixed in free space. At every point on the curve shown, the net electrostatic potential created by these charges is V. Find the separation r between the charges.
 .
.
View SolutionTwo charge +aq and -q are kept apart. Then , at any point on the right bisector of line joining the two charge
View SolutionTwo point charges Q1=400μCand Q2=100μC are kept fixed, 60 cm apart in vacuum. Find intensity of the electric field at midpoint of the line joining Q1 and Q2.
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View Solution
