A body of mass m is thrown straight up with velocity v0(v0<<ve) Find the velocity v with which the body comes down if the air drag equals kv2, where k is a positive constant and v is the velocity of the body.
The correct Answer is:A, B
To solve the problem, we need to analyze the motion of a body thrown upwards and then coming down under the influence of gravity and air drag. Here are the steps to derive the expression for the velocity v with which the body comes down:
Step 1: Analyze the upward motion
When the body is thrown upwards with an initial velocity v0, it experiences two forces:
1. The gravitational force acting downward, mg.
2. The air drag acting downward, which is given by kv2.
Using Newton's second law, we can write the equation of motion for the upward journey:
mdvdt=−mg−kv2
This can be rearranged to:
dvdt=−g−kmv2
Step 2: Integrate the upward motion
To find the maximum height h, we can use the relationship between velocity and displacement. We can rewrite the equation as:
mvdvds=−mg−kv2
Rearranging gives:
mvdvds=−mg−kv2
Integrating from v0 to 0 (the maximum height) gives:
∫0v0vdv=−∫h0(g+kmv2)ds
Step 3: Solve for maximum height
After integrating and simplifying, we find the maximum height h:
h=m2kln(1+kv20mg)
Step 4: Analyze the downward motion
When the body falls back down, the forces acting on it are:
1. The gravitational force mg acting downward.
2. The air drag kv2 acting upward.
The net force equation during the downward motion is:
mdvdt=mg−kv2
This can be rearranged to:
dvdt=g−kmv2
Step 5: Integrate the downward motion
Using the same approach as before, we can write:
mvdvds=mg−kv2
Rearranging gives:
dvg−kmv2=dsm
Integrating from 0 to v (the final velocity when it hits the ground) gives:
∫v0dvg−kmv2=1m∫h0ds
Step 6: Solve for final velocity
After integrating and applying limits, we can derive the expression for the velocity v when the body comes down:
v=v0√1+kv20mg
Final Answer
The velocity v with which the body comes down is:
v=v0√1+kv20mg
When the body is thrown upwards with an initial velocity v0, it experiences two forces:
1. The gravitational force acting downward, mg.
2. The air drag acting downward, which is given by kv2.
mdvdt=−mg−kv2
This can be rearranged to:
dvdt=−g−kmv2
To find the maximum height h, we can use the relationship between velocity and displacement. We can rewrite the equation as:
mvdvds=−mg−kv2
Rearranging gives:
mvdvds=−mg−kv2
Integrating from v0 to 0 (the maximum height) gives:
∫0v0vdv=−∫h0(g+kmv2)ds
After integrating and simplifying, we find the maximum height h:
h=m2kln(1+kv20mg)
When the body falls back down, the forces acting on it are:
1. The gravitational force mg acting downward.
2. The air drag kv2 acting upward.
mdvdt=mg−kv2
This can be rearranged to:
dvdt=g−kmv2
Using the same approach as before, we can write:
mvdvds=mg−kv2
Rearranging gives:
dvg−kmv2=dsm
Integrating from 0 to v (the final velocity when it hits the ground) gives:
∫v0dvg−kmv2=1m∫h0ds
After integrating and applying limits, we can derive the expression for the velocity v when the body comes down:
v=v0√1+kv20mg
The velocity v with which the body comes down is:
v=v0√1+kv20mg
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3120videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.329videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.2920videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A particle of mass m is projected upword with velocity v=ve2 (ve) escape of the particle is
View SolutionA body of mass m is thrown upwards at an angle θ with the horizontal with velocity v. While rising up the velocity of the mass after t second will be
View SolutionA smooth sledge is moving with constant velocity v0 toward left. A block is pushed toward right with a velocity v0’ (relative to ground).

(A) Find the velocity with which the block escapes from the sledge and necessary critical v0 for escaping from the sledge
(B) Will the block launch onto the sledge again?View SolutionA particle having a velocity v=v0 at t=0 is decelerated at the rate |a|=α√v, where α is a positive constant.
View SolutionA body is thrown with a velocity equal to n times the escape velocity (ve). Velocity of the body at large distance away will be :-
View Solution
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:View SolutionA motor boat of mass m moves along a lake with velocity v0. At t = 0, the engine of the boat is shut down. Resistance offered to the boat is equal to σv2. Then distance covered by the boat when its velocity becomes v0/2 is
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is
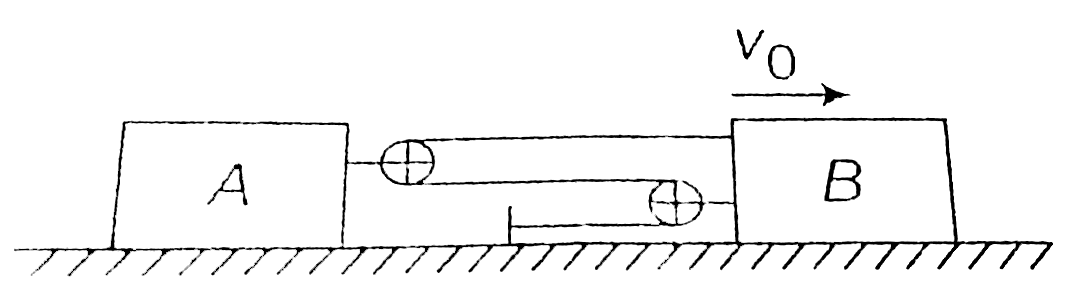 View Solution
View SolutionA body of mass m2 moving with velocity v0 collides elastically with another mass of m3 . Find % change in KE of first body
View SolutionA particle of mass m is projected upwards with velocity v=ve2, where ve is the escape velocity then at the maximum height the potential energy of the particle is : (R is radius of earth and M is mass of earth)
View Solution

