The dimension of stooping potential V0 in photoelectric effect In units of Planck's constant 'h', speed of light 'c' and Gravitational constant 'G' and ampere A is:
Option1 h1/3G2/3c1/3A−1
Option2 h2G3/2c1/3A−1
Option3 h0c5G−1A−1
Option4 h−2/3c−1/3G4/3A−1
To find the dimensions of the stopping potential V0 in terms of Planck's constant h, speed of light c, gravitational constant G, and the ampere A, we will follow these steps:
Step 1: Write the relationship for stopping potential
We can express the stopping potential V0 in terms of the constants as follows:
V0=khacbGcAd
where k is a dimensionless constant and a,b,c,d are the powers we need to determine.
Step 2: Identify the dimensions of each quantity
- The dimension of potential V0 is:
(V0)=(M1L2T−3A−1)
- The dimension of Planck's constant h is:
(h)=(M1L2T−1)
- The dimension of speed of light c is:
(c)=(L1T−1)
- The dimension of gravitational constant G is:
(G)=(M−1L3T−2)
- The dimension of ampere A is:
(A)=(A1)
Step 3: Write the dimensions of the right-hand side
Now substituting the dimensions into the equation:
(M1L2T−3A−1)=(M1L2T−1)a⋅(L1T−1)b⋅(M−1L3T−2)c⋅(A1)d
Step 4: Expand the right-hand side
Expanding the right-hand side gives:
(M1L2T−3A−1)=(Ma−cL2a+b+3cT−a−b−2cAd)
Step 5: Set up equations for each dimension
Now we can equate the dimensions from both sides:
1. For mass M:
a−c=1(1)
2. For length L:
2a+b+3c=2(2)
3. For time T:
−a−b−2c=−3(3)
4. For ampere A:
d=−1(4)
Step 6: Solve the equations
From equation (4), we have d=−1.
Now we can solve equations (1), (2), and (3):
- From equation (1): a=c+1
- Substitute a in equation (2):
2(c+1)+b+3c=2⟹2c+2+b+3c=2⟹5c+b=0⟹b=−5c
- Substitute a and b in equation (3):
−(c+1)−(−5c)−2c=−3⟹−c−1+5c−2c=−3⟹2c−1=−3⟹2c=−2⟹c=−1
- Now substitute c=−1 back to find a and b:
a=−1+1=0
b=−5(−1)=5
Step 7: Final values
We have:
- a=0
- b=5
- c=−1
- d=−1
Conclusion
The relation for the stopping potential V0 is:
V0=kh0c5G−1A−1
Thus, the dimensions of stopping potential V0 in terms of h,c,G,A is:
V0=kc5GA
We can express the stopping potential V0 in terms of the constants as follows:
V0=khacbGcAd
where k is a dimensionless constant and a,b,c,d are the powers we need to determine.
- The dimension of potential V0 is:
(V0)=(M1L2T−3A−1)
- The dimension of Planck's constant h is:
(h)=(M1L2T−1)
- The dimension of speed of light c is:
(c)=(L1T−1)
- The dimension of gravitational constant G is:
(G)=(M−1L3T−2)
- The dimension of ampere A is:
(A)=(A1)
Now substituting the dimensions into the equation:
(M1L2T−3A−1)=(M1L2T−1)a⋅(L1T−1)b⋅(M−1L3T−2)c⋅(A1)d
Expanding the right-hand side gives:
(M1L2T−3A−1)=(Ma−cL2a+b+3cT−a−b−2cAd)
Now we can equate the dimensions from both sides:
1. For mass M:
a−c=1(1)
2. For length L:
2a+b+3c=2(2)
3. For time T:
−a−b−2c=−3(3)
4. For ampere A:
d=−1(4)
From equation (4), we have d=−1.
- From equation (1): a=c+1
- Substitute a in equation (2):
2(c+1)+b+3c=2⟹2c+2+b+3c=2⟹5c+b=0⟹b=−5c
- Substitute a and b in equation (3):
−(c+1)−(−5c)−2c=−3⟹−c−1+5c−2c=−3⟹2c−1=−3⟹2c=−2⟹c=−1
- Now substitute c=−1 back to find a and b:
a=−1+1=0
b=−5(−1)=5
We have:
- a=0
- b=5
- c=−1
- d=−1
The relation for the stopping potential V0 is:
V0=kh0c5G−1A−1
Thus, the dimensions of stopping potential V0 in terms of h,c,G,A is:
V0=kc5GA
Topper's Solved these Questions
Similar Questions
Knowledge Check
The dimension of the quantity 1ε0e2hc is (e charge of electron,h Planck's constant and c=velocity of light)
A[M−1L−3T2A]B[M0L0T0A0]C[ML3T−4A−2]D[M−1L−3T4A2]
h d G has the dimensions of (h = height , d = density , G = Gravitational constant)
View SolutionThe dimensions of length are expressed as Gxcyhz, where G, c and h are the universal gravitational constant, speed of light and Planck's constant respectively, then :
View SolutionExpression for time in terms of G (universal gravitational constant), h (Planck constant) and c (speed of light) is proportional to:
View SolutionThe dimensions of Stefan-Boltzman constant σ can be written in terms of Plank's constant h. Boltzmann constant kB and the speed of light c as σ=hαKbBcY. Here
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectric effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejected electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Absorbed energy - Work function
12mv2max=h(v)−h(vn)=hv[1λ−1λn]
Where vn and λ0 are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if V0 is the stopping potential eV0=h(v−v0)
In the photoelectric currect effect the shape of strainght line graph between stopping potential (V0) and frequency of incident light (V) gves
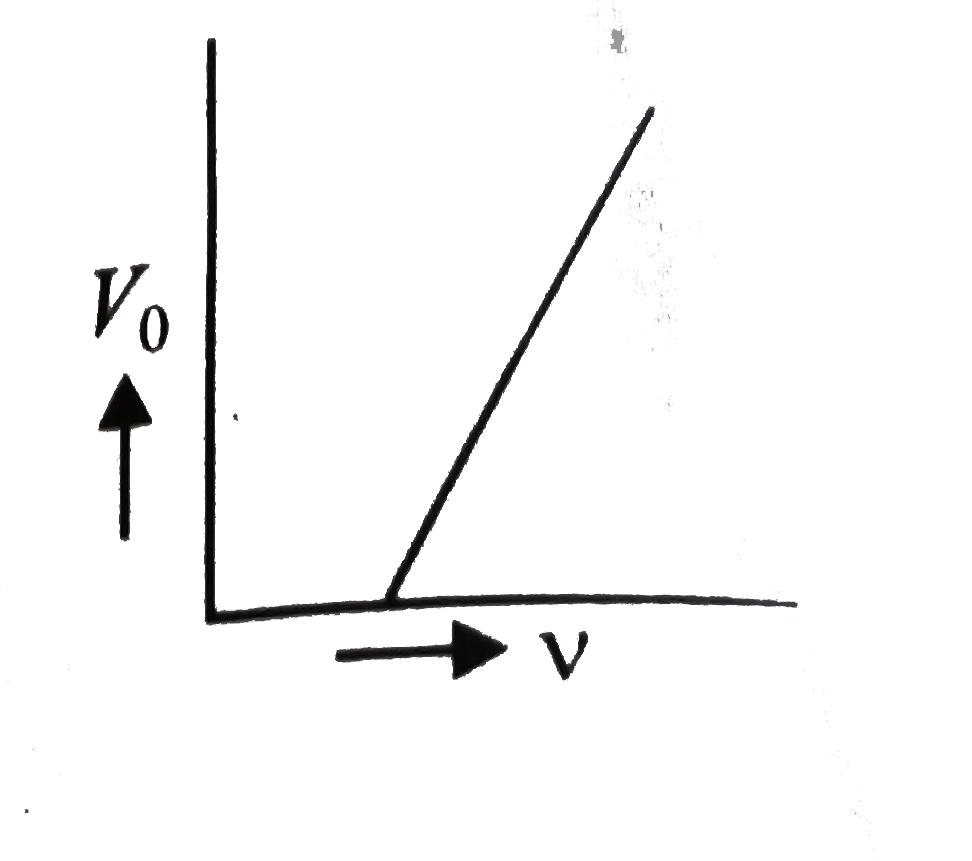
View Solution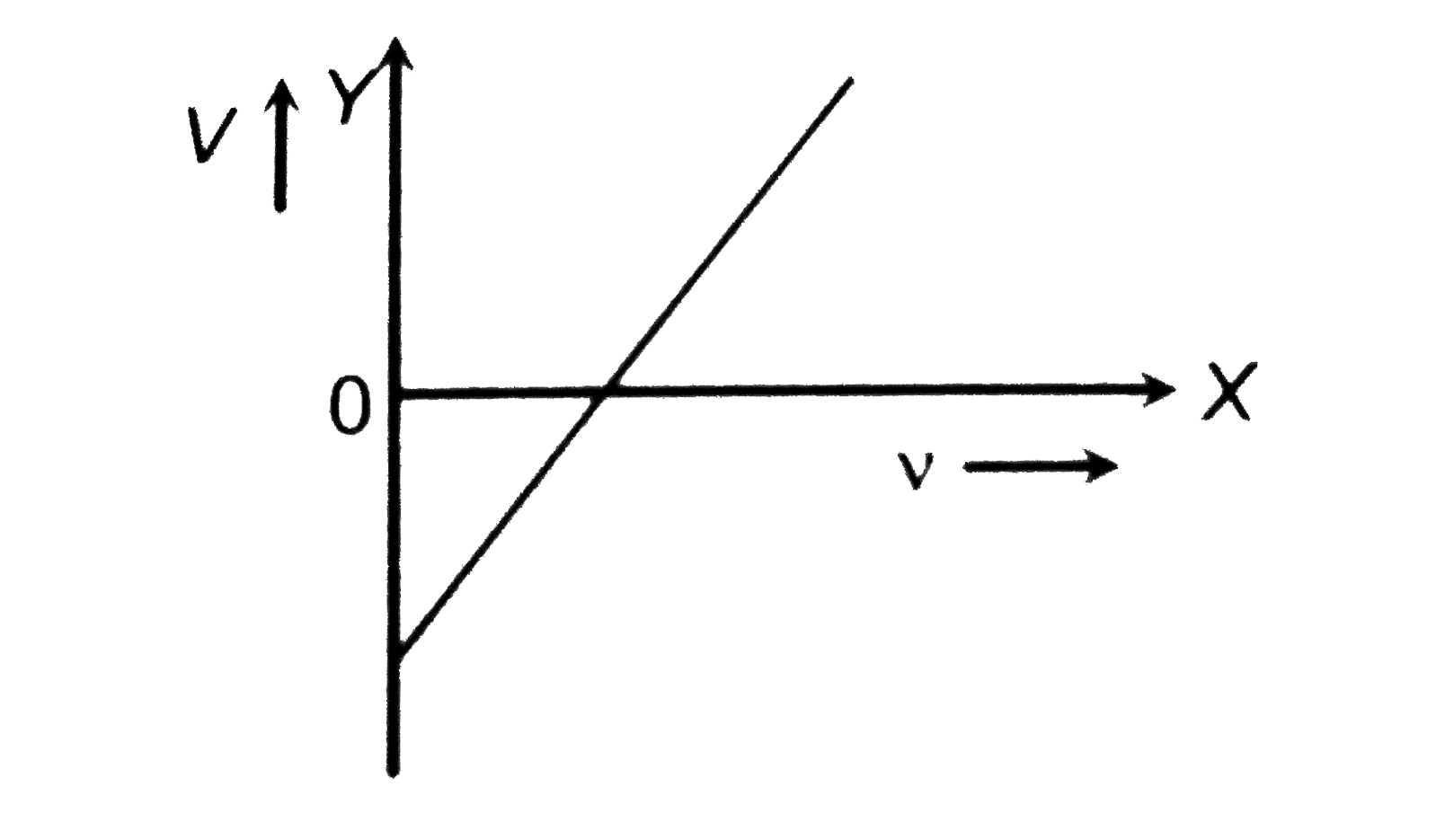
The stopping potential V for photoelectric emission from a metal surface is plotted along Y - axis and frequency v of incident light along X - axis . A straight line is obtained as shown . Planck's constant is given by
View SolutionThe stopping potential V for photoelectric emission from a metal surface is plotted along Y - axis and frequency v of incident light along X - axis . A straight line is obtained as shown . Planck's constant is given by

View Solution
