The dimension of σb4 (where σ is Stefan's constant and b is Wien's constant) are [ML4T−3] is it true.
[M0L0T0]
[ML4T−3]
[ML−2T]
[ML6T−3]
The correct Answer is:B
To determine if the dimension of σb4 is indeed (ML4T−3), we will calculate the dimensions of both Stefan's constant (σ) and Wien's constant (b) step by step.
Step 1: Determine the Dimensions of Stefan's Constant (σ)
Stefan's constant (σ) is defined as:
σ=EA⋅T4
Where:
- E is energy,
- A is area,
- T is temperature.
Dimensions of Energy (E):
The dimension of energy is given by:
(E)=(ML2T−2)
Dimensions of Area (A):
The dimension of area is:
(A)=(L2)
Dimensions of Temperature (T):
The dimension of temperature is:
(T)=(K)
Putting it all together:
Now substituting these into the equation for σ:
(σ)=(E)(A)⋅(T4)=(ML2T−2)(L2)⋅(K4)=(ML2T−2)(L2K4)
Simplifying this gives:
(σ)=(M)(L2)(T−2)(L−2)(K−4)=(M)(T−2)(K−4)
Thus, the dimensions of σ are:
(σ)=(MT−3K−4)
Step 2: Determine the Dimensions of Wien's Constant (b)
Wien's constant (b) is defined in relation to the wavelength (λ) and temperature (T) as:
λ=bT
Rearranging gives:
b=λ⋅T
Dimensions of Wavelength (λ):
The dimension of wavelength is:
(λ)=(L)
Putting it all together:
Now substituting into the equation for b:
(b)=(L)(K)=(LK)
Step 3: Calculate the Dimensions of σb4
Now we can calculate the dimensions of σb4:
(σb4)=(σ)⋅(b4)=(MT−3K−4)⋅(L4K4)
Simplifying this expression:
(σb4)=(M)(T−3)(K−4)(L4)(K4)=(M)(L4)(T−3)(K0)
Since K0=1, we can ignore it:
(σb4)=(M)(L4)(T−3)
Conclusion
Thus, the final dimensions of σb4 are:
(σb4)=(ML4T−3)
This confirms that the statement in the question is true.
---
- E is energy,
- A is area,
- T is temperature.
The dimension of energy is given by:
The dimension of area is:
The dimension of temperature is:
Now substituting these into the equation for σ:
The dimension of wavelength is:
Now substituting into the equation for b:
(σb4)=(M)(T−3)(K−4)(L4)(K4)=(M)(L4)(T−3)(K0)
Topper's Solved these Questions
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE
17 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
Similar Questions
Knowledge Check
The number of sigma (σ) and pi (π) bonds in pent-2-en-4-yne is :
A11 σ bonds and 2 π bondsB13 σ bonds and no π bondsC10 σbonds and 3 π bondsD8 σ bonds and 5π bonds.
The dimensions of Stefan-Boltzman constant σ can be written in terms of Plank's constant h. Boltzmann constant kB and the speed of light c as σ=hαKbBcY. Here
View SolutionThe radiation emitted per unit time by unit area of a black body at temperature T is σT4 wehre σ is the Stefan-Boltzmann constant. The constant σ can also be expressed in terms of Boltmann's constant (k), Planck's constant (h) and speed of light (3) as σ=Akαhβcγ where A,α,β and γ are dimensionless constants. The set (α,β,γ) is givne by
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
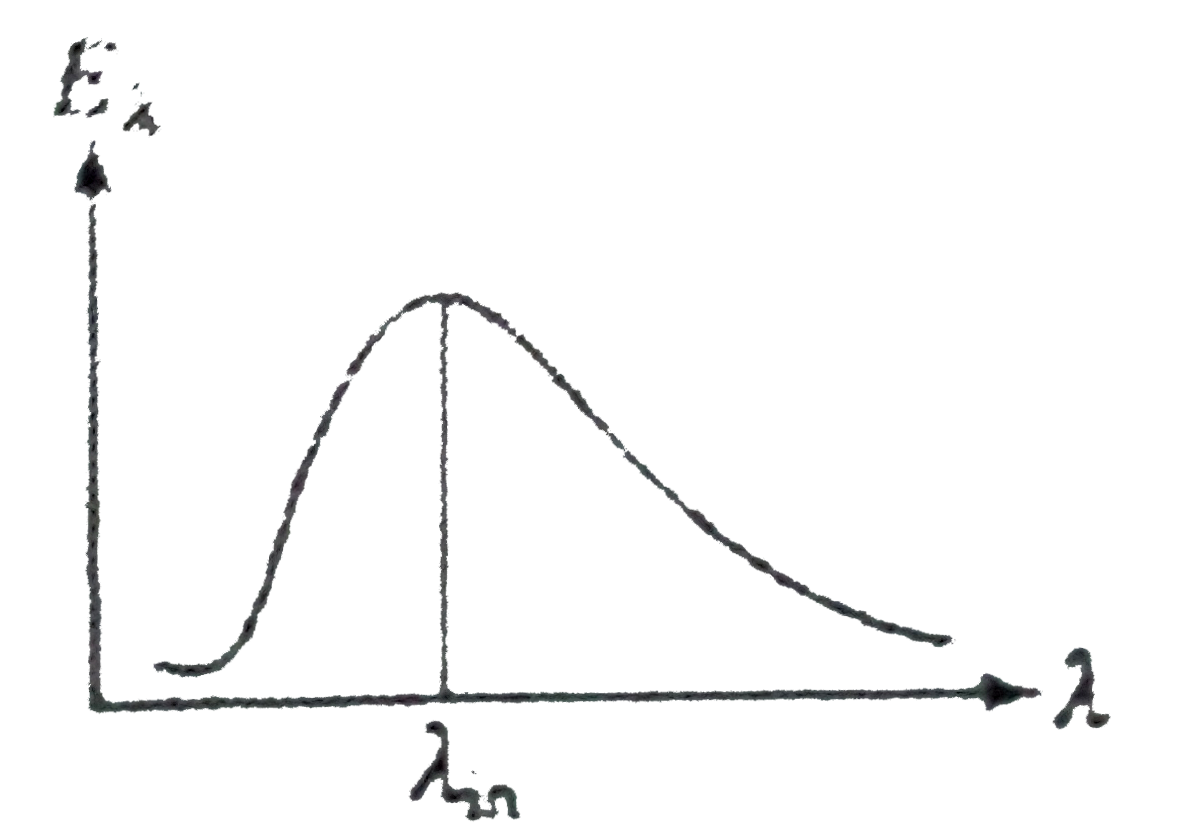
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) is
View SolutionThe radiations emitted by the sun are analyzed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
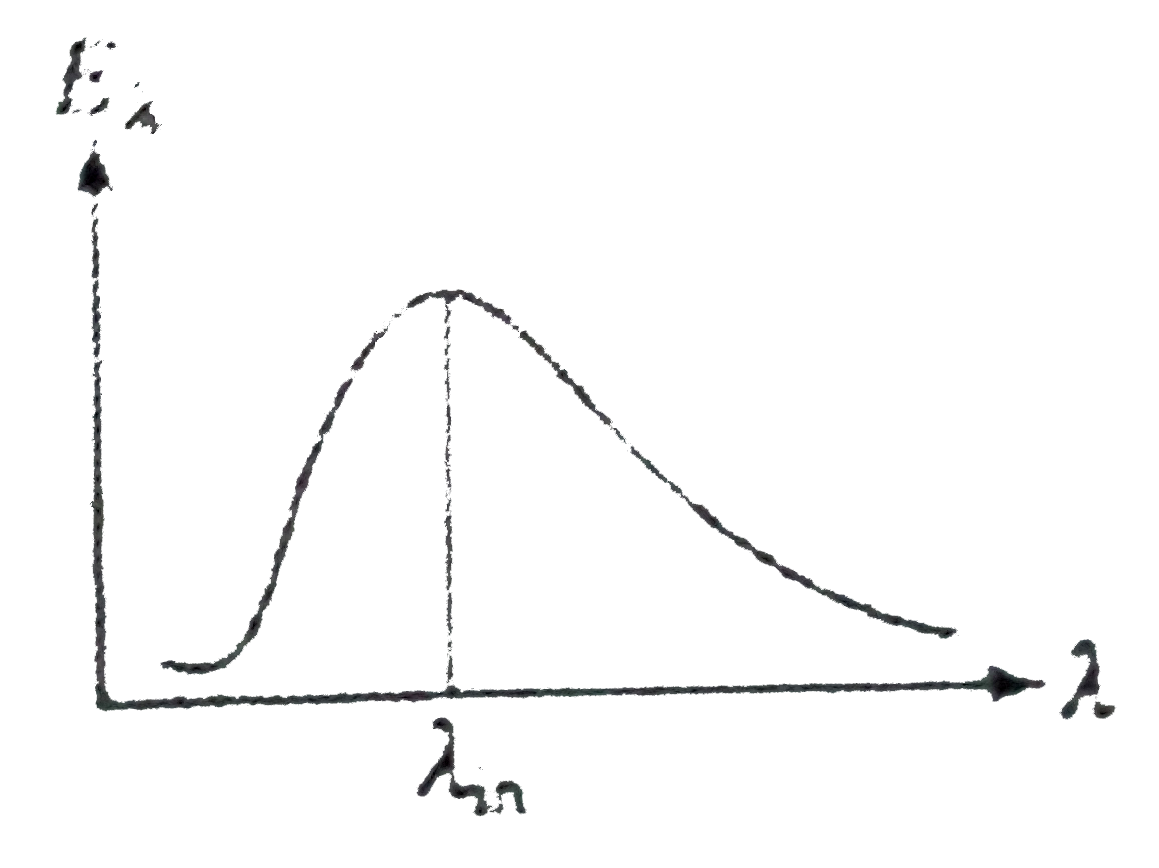
Assume the sun produces energy only by nuclear fusion of hydrogen nuclei and the fraction of nuclear mass of hydrogen that can be converted to energy is η. How long will the sun keep on emittied the energy if the mass of hydrogen at present in Sun's core is m?
View SolutionThe ratio of Van Der Waal's constants a and b, (ab) has the dimension of :
View SolutionThe correct order in which the dimensions of ''time'' decreases in the following physical quantities is
(A) Stefan's constant
(B) Coeffecient of volume expansion
(C ) Work
(D) Velocity gradient
View SolutionObtain the dimensions of (1) coefficient of thermal conductivity (2) Gas constant (3) Boltzmann constant (4) Planck's constant.
View Solution
