A liquid is contain in a vertical tube of semicircular cross section figure. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
2:π
1:π
3:π
2.7:π
The correct Answer is:A
Effective length of flat part = 2r
Effective length of curved part is πr
So, required ratio is 2:π
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.59
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.60
8 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.57
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A uniform vertical tube of circular cross section contains a liquid. The contact angle is 90∘. Consider a diameter of the tube lying in the surface of the liquid. The surface of the right of this diameter pulls the surface on the left of it. What keeps the surface on the left in equilibrium?
View SolutionA liquid is coming out from a vertical tube. The relation between the weight of the drop W , surface tension of the liquid T and radius of the tube r is given by, if the angle of contact is zero
View SolutionDiameter of the flat surface of a circular plano-convex lens is 6cm and thickness at the centre is 3mm. The radius of curvature of the curved part is
View SolutionA particle slides along a track with elevated ends and a flat central part as shown in figure. The flat part has a length l=3m. The curved portions of the track are frictionless. For the flat part, the coefficient of kinetic friction is μk=0.2. The particle is released at point A which is at height h=1.5m above the flat part of the track. Where does the particle finally come to rest?
View SolutionA solid hemisphere of radius R is made to just sink in a liquid of density ρ. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.
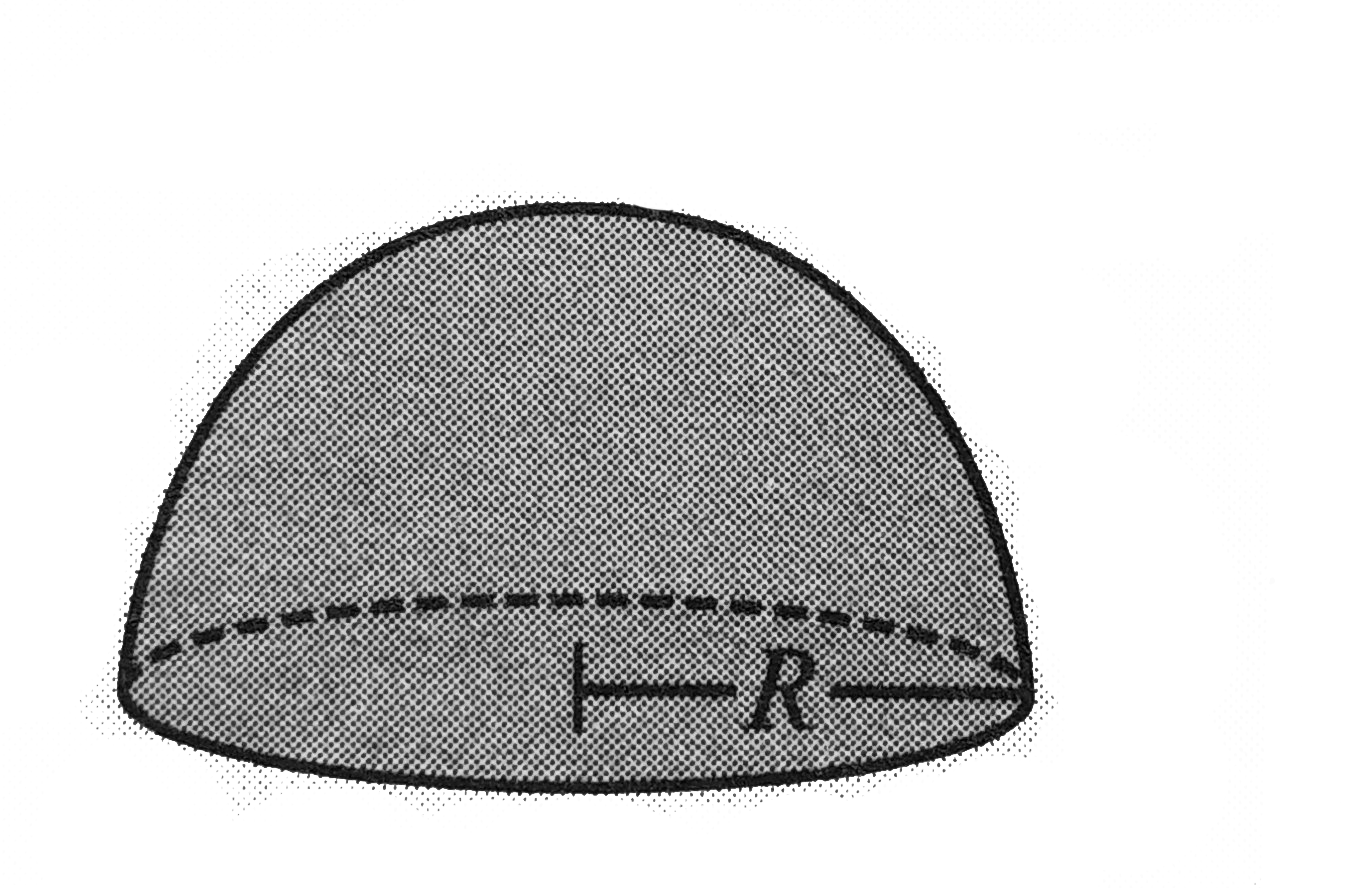View SolutionA long glass capillary (radius R) is taken out of liquid (surface tension S and density ρ) in vertical position. Angle of contact everywhere is zero. Atmospheric pressure is P0. It is observed that the capillary retains some liquid.
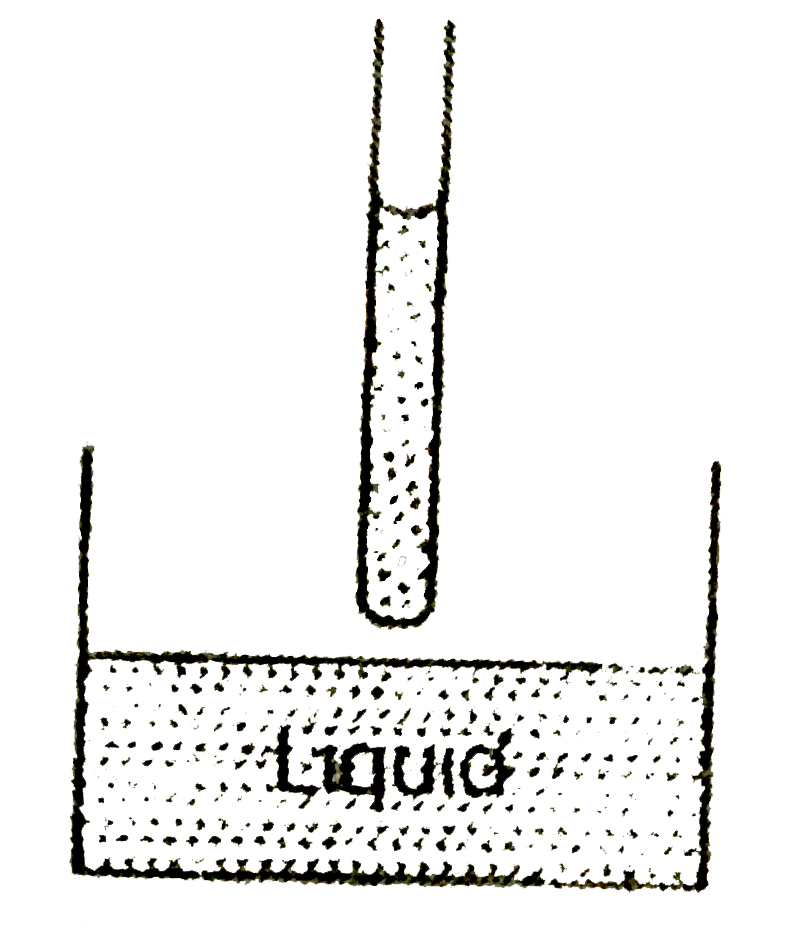
The radius of curvature of meniscus at the bottom of tube is
View SolutionWhen a vertical capillary of length l with a sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature in this process remains constant.)
View SolutionWhen a vertical capillary of length with the sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature this process remains constant.)
View SolutionA long glass capillary (radius R) is taken out of liquid (surface tension S and density ρ) in vertical position. Angle of contact everywhere is zero. Atmospheric pressure is P0. It is observed that the capillary retains some liquid.
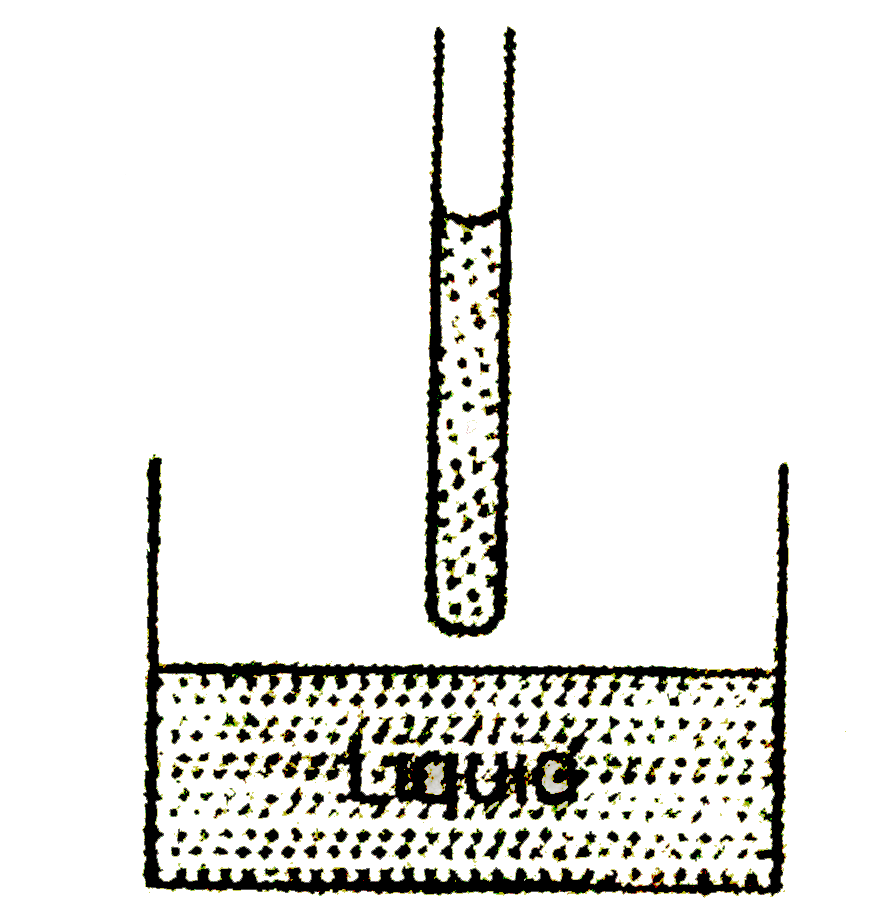
The length of liquid column retained in the capillary is
View SolutionTwo equal and opposite point forces applied at mid- points of the ends of a rod of square cross shown. Consider the dotted section ABCD. If the rod is cut across this Gloss section, the force exerted by the right part of the rod on left part across this cross section is
View Solution