The moment of inertia of a thin sheet of mass M of the given shape about the specified axis is ( axis and sheet both are in same plane )
A. 32Ma2
B. 34Ma2
C. 712Ma2
D. 13Ma2
a. 32Ma2
b. 3/4 Ma^2
712Ma2
13Ma2
The correct Answer is:B
To solve the problem of finding the moment of inertia of a thin sheet of mass M about a specified axis in the same plane as the sheet, we will follow these steps:
Step 1: Understand the Geometry
We have a thin sheet in the shape of a square with side length a. The axis of rotation is a diagonal of the square, which makes an angle of 45 degrees with the horizontal.
Step 2: Moment of Inertia About the Center
The moment of inertia of a square sheet about an axis through its center and parallel to one of its sides is given by:
IO=112Ma2
where M is the mass of the sheet and a is the side length of the square.
Step 3: Apply the Parallel Axis Theorem
Since we want to find the moment of inertia about the diagonal axis (let's denote it as IP), we can use the parallel axis theorem:
IP=IO+Md2
where d is the distance from the center of mass to the new axis of rotation.
Step 4: Calculate the Distance d
The distance d from the center of the square to the diagonal can be calculated as follows. The diagonal of the square divides it into two equal triangles, and the distance from the center to the diagonal can be found using the formula for the distance from a point to a line. For a square of side a, the distance d from the center to the diagonal is:
d=a√2
Step 5: Substitute d into the Equation
Now, substituting d into the parallel axis theorem:
IP=112Ma2+M(a√2)2
Calculating (a√2)2:
(a√2)2=a22
Thus, substituting this back into the equation gives:
IP=112Ma2+M⋅a22
Step 6: Combine the Terms
Now, we need a common denominator to combine the terms:
IP=112Ma2+612Ma2=712Ma2
Conclusion
Thus, the moment of inertia of the thin sheet about the specified axis is:
IP=712Ma2
The correct answer is option C: 712Ma2.
---
We have a thin sheet in the shape of a square with side length a. The axis of rotation is a diagonal of the square, which makes an angle of 45 degrees with the horizontal.
The moment of inertia of a square sheet about an axis through its center and parallel to one of its sides is given by:
Since we want to find the moment of inertia about the diagonal axis (let's denote it as IP), we can use the parallel axis theorem:
The distance d from the center of the square to the diagonal can be calculated as follows. The diagonal of the square divides it into two equal triangles, and the distance from the center to the diagonal can be found using the formula for the distance from a point to a line. For a square of side a, the distance d from the center to the diagonal is:
Now, substituting d into the parallel axis theorem:
Now, we need a common denominator to combine the terms:
Thus, the moment of inertia of the thin sheet about the specified axis is:
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.599videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.608videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.579videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions

Find moment of inertia of a thin sheet of mass M in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is LView SolutionFor a circular cardboard of uniform thickness and mass M, a square disc of the maximum possible are is cut. If the moment of inertia of the square with the moment of inertial of the square with the axis of rotation at the centre and perpendicular to the plane of the disc is Ma26, the radius of the circular cardboard is
View SolutionMoment of inertia of a thin semicircular disc (mass−M&radius=R) about an axis through point O and perpendicular to plane of disc, is given by :
 .View Solution
.View SolutionMoment of inertia of a thin semicircular disc (mass−M&radius=R) about an axis through point O and perpendicular to plane of disc, is given by :
 .View Solution
.View SolutionThe velocity of the centre of mas of the system of two particle each of mass 2kg, as shown in figure, is
 View Solution
View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View SolutionThe moment of inertia of a thin square plate ABCD, fig, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is
where l1,l2,l3andl4 are respectively the moments of intertial about axis 1,2,3 and 4 which are in the plane of the plate.
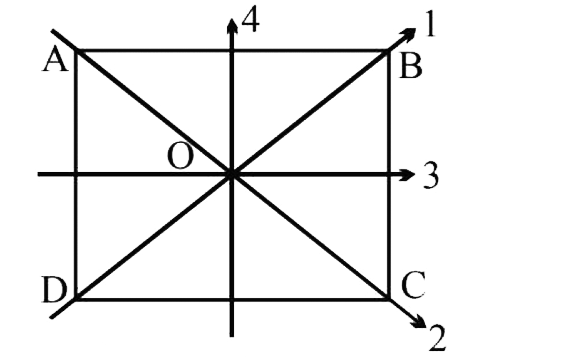 View Solution
View SolutionA solid sphere of mas 2kg rolls on a table with linear speed of 1m/s. Its total kinetic energy is
View SolutionWhat is the moment of inertia of a
(i) uniform circular ring of mass 2 kg about its 4 m diameter ?
(ii) a thin disc about an axis coinciding with a diameter ?View SolutionA symmetric lamina of mass M consists of a square shape with a semicircular section over each of the edge of the square as in fig. The side of the square is 2a.
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma2. The moment of inertia of the lamina about the tangent AB in the plane of lamina is.
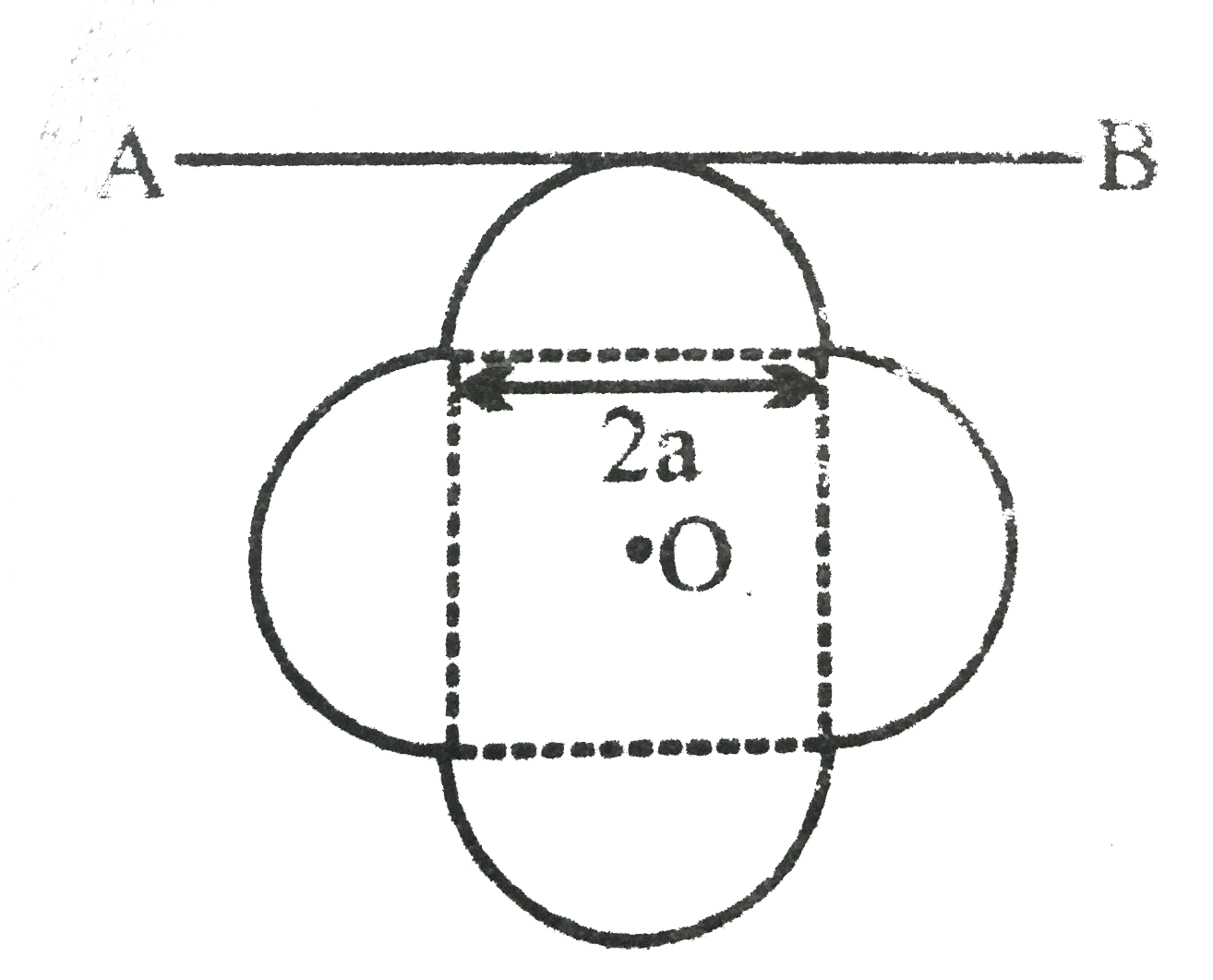 .View Solution
.View Solution

