A 25kg uniform solid with a 20cm radius respectively by a verticle wire such then the point suspended is velocity about the center of the sphere torque of 0.10N-m and then montain the sphere then at angle of 1.0 rad if sphere is then released its period of the oscillation will be
π second
√2π second
2π second
4π second
The correct Answer is:D
To solve the problem step by step, we will follow the given information and apply the relevant physics concepts.
Step 1: Understand the Given Information
- Mass of the sphere (m) = 25 kg
- Radius of the sphere (r) = 20 cm = 0.2 m
- Torque (τ) = 0.10 N·m
- Angle (θ) = 1.0 rad
Step 2: Relate Torque to Torsional Constant
The relationship between torque (τ) and the angular displacement (θ) is given by:
τ=−kθ
Where:
- k is the torsional constant of the wire.
Taking the magnitude, we can write:
0.10=k⋅1.0
Thus, we find:
k=0.10N⋅m/rad
Step 3: Calculate the Moment of Inertia (I)
The moment of inertia (I) for a solid sphere is given by:
I=25mr2
Substituting the values:
I=25⋅25kg⋅(0.2m)2
Calculating:
I=25⋅25⋅0.04=25⋅1=25kg⋅m2
Step 4: Calculate the Time Period of Oscillation (T)
The time period (T) of oscillation for a torsional pendulum is given by:
T=2π√Ik
Substituting the values of I and k:
T=2π√250.10
Calculating:
T=2π√25⋅0.10=2π√20.5=2π√4=2π⋅2=4πseconds
Final Answer
The time period of the oscillation when the sphere is released is:
T=4πseconds
---
- Mass of the sphere (m) = 25 kg
- Radius of the sphere (r) = 20 cm = 0.2 m
- Torque (τ) = 0.10 N·m
- Angle (θ) = 1.0 rad
The relationship between torque (τ) and the angular displacement (θ) is given by:
τ=−kθ
Where:
- k is the torsional constant of the wire.
0.10=k⋅1.0
Thus, we find:
k=0.10N⋅m/rad
The moment of inertia (I) for a solid sphere is given by:
I=25mr2
Substituting the values:
I=25⋅25kg⋅(0.2m)2
Calculating:
I=25⋅25⋅0.04=25⋅1=25kg⋅m2
The time period (T) of oscillation for a torsional pendulum is given by:
T=2π√Ik
Substituting the values of I and k:
T=2π√250.10
Calculating:
T=2π√25⋅0.10=2π√20.5=2π√4=2π⋅2=4πseconds
The time period of the oscillation when the sphere is released is:
T=4πseconds
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.65
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.66
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.63
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A uniform solid sphere of mass m and radius R is suspended in vertical plane from a point on its periphery. The time period of its oscillation is
View SolutionMetallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
View SolutionMetallic spheres of radii 6 cm, 8 cm and 10 cm respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
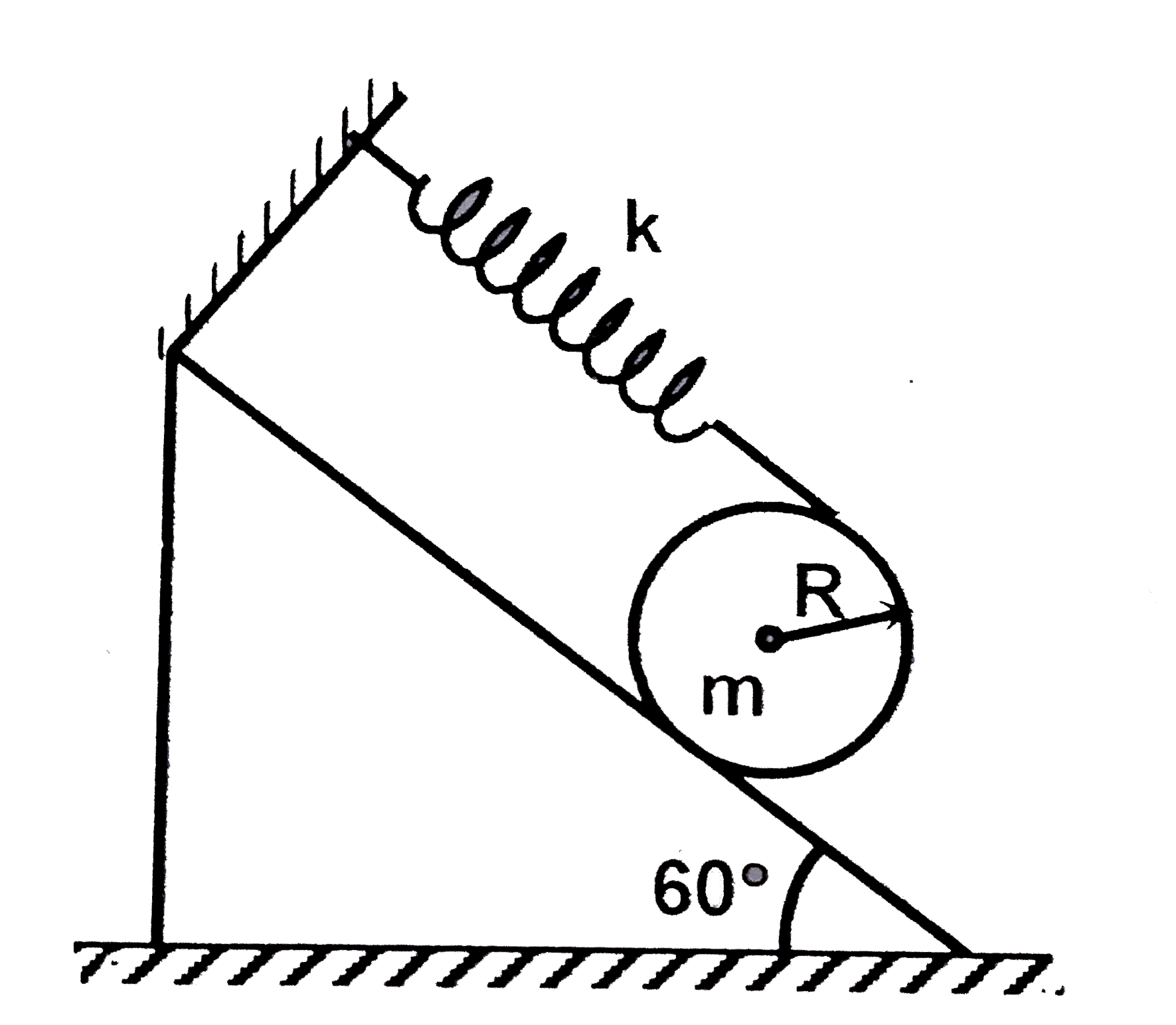
View SolutionA uniform solid sphere of mass 'm' and radius R is in equilibrium on an inclined plane by the action of the light spring of stiffness k, gravity and on it. If the angle of inclination of the plane is 60∘, then find the time period of oscillation for small displancement.
View SolutionA sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
View SolutionA solid sphere of diameter 0.1 m and 5 kg is rolling down an inclined plane with a speed of 4 m/s. The total kinetic energy of the sphere is :
View SolutionA uniformly charged solid sphere a mass M, radius R having charge Q is rotated about its diameter with frequency f0. The magnetic moment of the sphere is
View SolutionA glass sphere has radius of 5.0cm and a refractive index of 1.6. A paperweight is constructed by slicing through the sphere on a plate that is 2.0cm from the centre of the sphere and perpendicular to radius of the sphere that passes through the centre of the circle formed by the intersection of the plane and the sphere. The paperweight is placed on a table and viewed from directly above an observer who is 8.0cm from the table top, as shown in figure. When viewed through the paperweight, how far away does the table top appear to the observer?
View SolutionA conducting sphere fo radius 10 cm has an unknown charge. If the electric field 20 cm from the center of the sphere is 1.5×103N/C and points radially inwards, what is the net charge on the sphere ?
View SolutionThe radius of a sphere is measured as (10±0.02%) cm. The error in the measurement of its volume is
View Solution
