Distance between a frog and an insect on a horizontal plane is 10m. Frog can jump with a maximum speed of . Minimum number of jumps required by the frog to catch the insect is : .
5
10
100
50
The correct Answer is:B
To solve the problem of how many jumps a frog needs to catch an insect located 10 meters away, we can follow these steps:
1. Identify Given Values:
- Distance between the frog and the insect, d=10m
- Maximum speed of the frog, umax=√10m/s
- Acceleration due to gravity, g=10m/s2
2. Calculate the Range of One Jump:
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
For maximum range, the angle θ should be 45∘, where sin(90∘)=1. Thus, the formula simplifies to:
Rmax=u2g
Substituting the values:
Rmax=(√10)210=1010=1m
3. Determine the Number of Jumps Required:
To find the minimum number of jumps n required to cover the distance d:
n⋅Rmax=d
Substituting the known values:
n⋅1=10
Therefore:
n=101=10
4. Conclusion:
The minimum number of jumps required by the frog to catch the insect is n=10.
Final Answer:
The minimum number of jumps required by the frog to catch the insect is 10 jumps.
---
- Distance between the frog and the insect, d=10m
- Maximum speed of the frog, umax=√10m/s
- Acceleration due to gravity, g=10m/s2
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
For maximum range, the angle θ should be 45∘, where sin(90∘)=1. Thus, the formula simplifies to:
Rmax=u2g
Substituting the values:
Rmax=(√10)210=1010=1m
To find the minimum number of jumps n required to cover the distance d:
n⋅Rmax=d
Substituting the known values:
n⋅1=10
Therefore:
n=101=10
The minimum number of jumps required by the frog to catch the insect is n=10.
The minimum number of jumps required by the frog to catch the insect is 10 jumps.
Topper's Solved these Questions
Similar Questions
A ball is thrown from a field with a speed of 12.0 m/s at an angle of 450 with the horizontal. At what distance will it hit the field again ? Take g=10.0ms2
View SolutionA ball is thrown at a speed of 20 m/s at an angle of 30∘ with the horizontal . The maximum height reached by the ball is
(Use g=10m/s2)View SolutionA ball is throw vertically upward. It has a speed of 10m/s when it has reached on half of its maximum height. How high does the ball rise ? (Taking g=10m/s2).
View SolutionIn the arrangement as shown, tension T2 is (g=10m/s2)
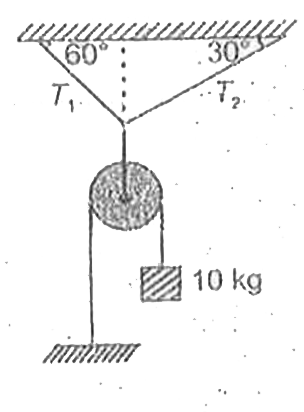 View Solution
View SolutionA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
View SolutionA ball is thrown up at a speed of 4.0 m/s. Find the maximum height reached by the ball. Take g=10m/s2.
View SolutionA ball is projected vertically up wards with a velocity of 100 m/s. Find the speed of the ball at half the maximum height. (g=10m/s2)
View SolutionA bus turns a slippery road having coefficient of friction of 0⋅5 with a speed of 10 m/s .The minimum radius of the arc in which bus turns is [ Take g = 10 ms2]
View SolutionA stone is thrown horizontally with a velocity of 10m/sec. Find the radius of curvature of it’s trajectory at the end of 3s after motion began. (g=10m/s2)
View SolutionA stone is thrown horizontally with a velocity of 10m/sec. Find the radius of curvature of it’s trajectory at the end of 3s after motion began. (g=10m/s2)
View Solution

