A circular disc X of radius R is made from an iron of thickness t, and another disc Y of radius 4R is made from an iron plate of thickness t/4. Then the relation between the moment of mertia Ix and IY is :
Iy=32Ix
Iy=16Ix
Iy=Ix
Iy=64Ix
The correct Answer is:D
To find the relation between the moments of inertia Ix and Iy for the two discs, we will follow these steps:
Step 1: Understand the Moment of Inertia Formula
The moment of inertia I of a disc about an axis passing through its center and perpendicular to its plane is given by the formula:
I=12MR2
where M is the mass of the disc and R is its radius.
Step 2: Calculate the Mass of Disc X
For disc X:
- Radius Rx=R
- Thickness tx=t
The volume Vx of disc X is given by:
Vx=Area×Thickness=πR2xtx=πR2t
The mass Mx of disc X can be calculated using the density ρ:
Mx=ρVx=ρπR2t
Step 3: Calculate the Moment of Inertia for Disc X
Now, substituting Mx into the moment of inertia formula:
Ix=12MxR2x=12(ρπR2t)R2=12ρπR4t
Step 4: Calculate the Mass of Disc Y
For disc Y:
- Radius Ry=4R
- Thickness ty=t4
The volume Vy of disc Y is:
Vy=πR2yty=π(4R)2(t4)=π(16R2)(t4)=4πR2t
The mass My of disc Y is:
My=ρVy=ρ(4πR2t)
Step 5: Calculate the Moment of Inertia for Disc Y
Now substituting My into the moment of inertia formula:
Iy=12MyR2y=12(ρ(4πR2t))(4R)2=12(ρ(4πR2t))(16R2)=322ρπR4t=16ρπR4t
Step 6: Find the Relation Between Ix and Iy
Now we have:
Ix=12ρπR4t
Iy=16ρπR4t
To find the ratio IxIy:
IxIy=12ρπR4t16ρπR4t=12⋅116=132
Thus, we can express Iy in terms of Ix:
Iy=32Ix
Final Result
The relation between the moments of inertia is:
Iy=32Ix
---
The moment of inertia I of a disc about an axis passing through its center and perpendicular to its plane is given by the formula:
I=12MR2
where M is the mass of the disc and R is its radius.
For disc X:
- Radius Rx=R
- Thickness tx=t
Vx=Area×Thickness=πR2xtx=πR2t
Mx=ρVx=ρπR2t
Now, substituting Mx into the moment of inertia formula:
Ix=12MxR2x=12(ρπR2t)R2=12ρπR4t
For disc Y:
- Radius Ry=4R
- Thickness ty=t4
Vy=πR2yty=π(4R)2(t4)=π(16R2)(t4)=4πR2t
My=ρVy=ρ(4πR2t)
Now substituting My into the moment of inertia formula:
Iy=12MyR2y=12(ρ(4πR2t))(4R)2=12(ρ(4πR2t))(16R2)=322ρπR4t=16ρπR4t
Now we have:
Ix=12ρπR4t
Iy=16ρπR4t
IxIy=12ρπR4t16ρπR4t=12⋅116=132
Iy=32Ix
The relation between the moments of inertia is:
Iy=32Ix
Topper's Solved these Questions
Similar Questions
A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is (about an axis passing through centre and perpendicular to the disc)
View SolutionA circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IAandIB is
View Solution
Knowledge Check
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
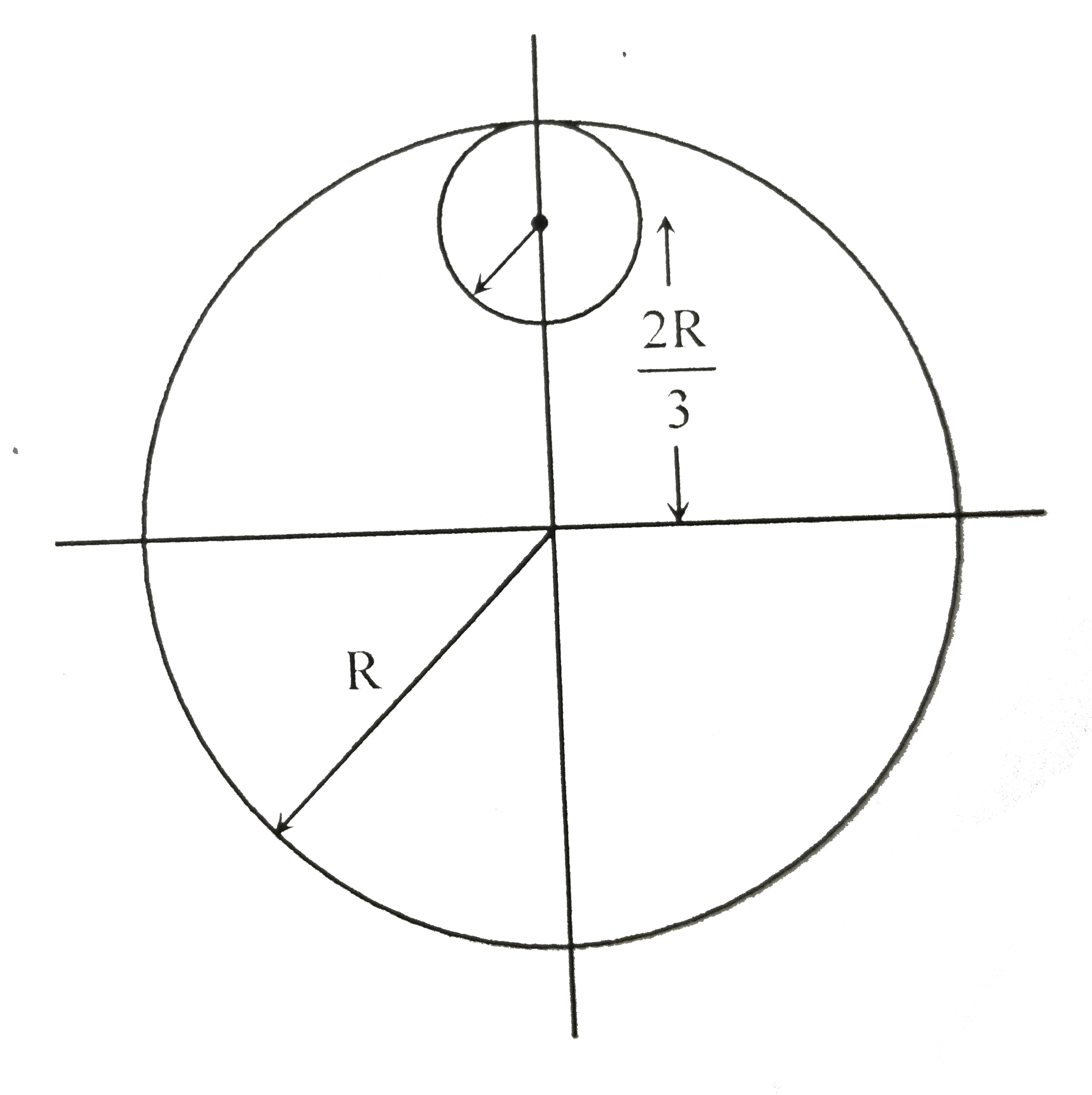 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
A uniform circular disc A of radius r is made from A copper plate of thickness t and another uniform circular disc B of radius 2r is made from a copper plate of thickness t/2. The relation between the moments of inertia IAandIB is?
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
View SolutionA circular disc of radius R and thickness R6 has moment of inertia I about its axis. If it is melted and casted into a solid sphere then what will be its moment of inertia, about its diametric axis?
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
View SolutionA concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View Solution
