The two ends of a rod of length L and a uniform cross -secontional area A are kept at two temperatures T1 and T2(T1>T2). The rate of heat tranfer, dQdt, through the rod in a steady state is given by
dQdt=KL(T1−T2)A
dQdt=K(T1−T2)LA
dQdt=KLA(T1−T2)
dQdt=KA(T1−T2)L
The correct Answer is:D
For a rod of length L and area of cross-section A whose faces are maintained at temperature T1 and T2 respectively.
Then in steady state the rate of heat flowing from one face to the other face in time t is given by
dQdt=KA(T1−T2)L
The curved surface of rod is kept insulated from surrounding to avoid leakage of heat
Topper's Solved these Questions
- HEAT TRANSFERBOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-2
1 Videos
- HEAT TRANSFERBOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-3
1 Videos
- HEAT TRANSFERBOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-1
1 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise
21 Videos
- KINEMATICSBOOK - RESONANCE ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise
65 Videos
Similar Questions
The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View SolutionTwo ends of a rod of non uniform area of cross section are maintained at temperature T1and T2 (T1>T2) as shown in the figure
If l is heat current through the cross-section of conductor at distance x from its left face, then the variation of l with x is best represented by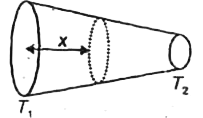
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View Solution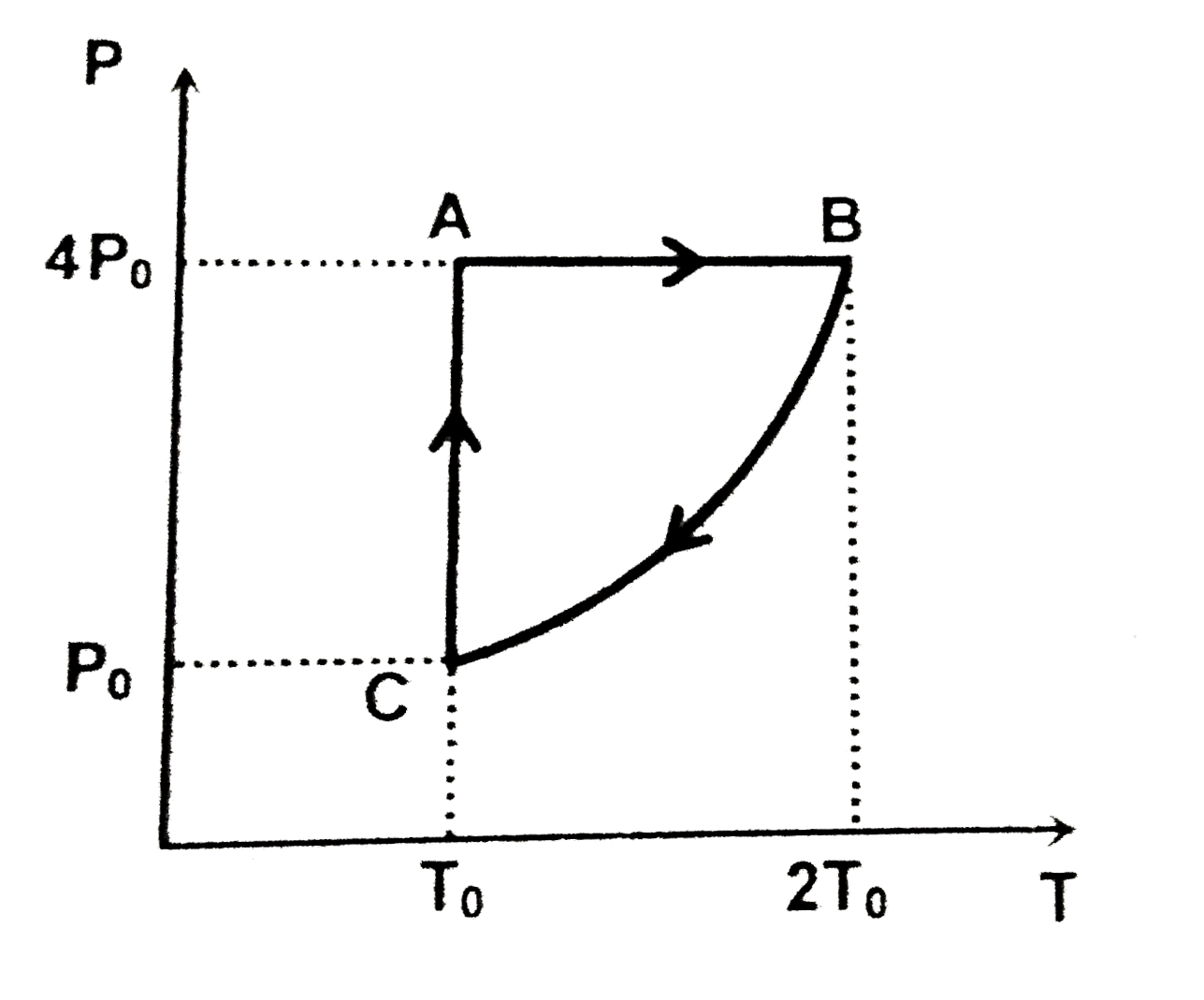
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
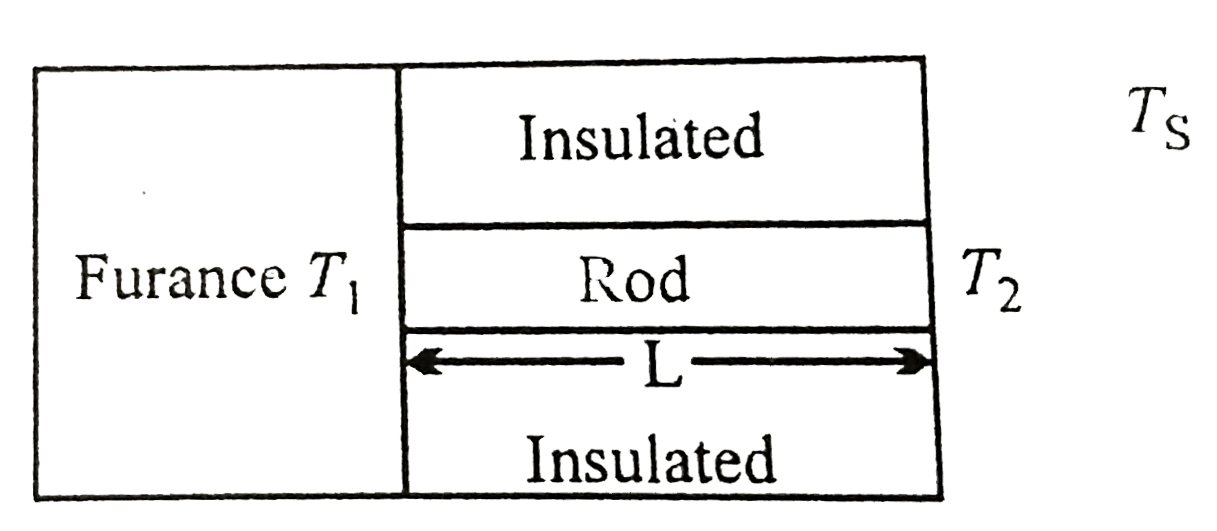
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-

View SolutionShown below are the black body radiation curves at temperature T1 and T2(T2>T1). Which of the following plots is correct?
View SolutionThe ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
View SolutionThe ends of a metal rod are kept at temperature θ1andθ2 with θ2>θ1. At steady state the rate of flow of heat along the rod is directly proportional to
View Solution
