In a series LCR circuit containing an AC voltage source of frequency ω, current and voltage are measured. Then for the resistance, consider the statements-
[a] current is maximum at ω2=1/LC
[b] current is minimum at ω2=1/LC
[c] voltage across R is maximum at ω2=1/LC
[d] voltage across R is minimum at ω2=1/LC
the voltage statement is
a and c are both correct
b and d are both correct
a and d are both correct
none of these
The correct Answer is:A
To analyze the statements regarding the behavior of current and voltage in a series LCR circuit at resonance, we can follow these steps:
Step 1: Understand Resonance in LCR Circuit
In a series LCR circuit, resonance occurs when the inductive reactance (XL) equals the capacitive reactance (XC). This condition can be mathematically expressed as:
ω2=1LC
where ω is the angular frequency, L is the inductance, and C is the capacitance.
Step 2: Analyze Current at Resonance
At resonance, the impedance of the circuit is minimized and is equal to the resistance R only. This results in the maximum current flowing through the circuit:
I=VR
where V is the voltage across the circuit. Therefore, the statement:
- (a) Current is maximum at ω2=1LC is true.
Step 3: Analyze Current Minimum Statement
The statement:
- (b) Current is minimum at ω2=1LC is false because, as established, the current is maximum at this frequency.
Step 4: Analyze Voltage Across Resistor
At resonance, the voltage across the resistor VR is also at its maximum because the entire source voltage appears across the resistor when the circuit is in resonance. Therefore, the statement:
- (c) Voltage across R is maximum at ω2=1LC is true.
Step 5: Analyze Voltage Minimum Statement
The statement:
- (d) Voltage across R is minimum at ω2=1LC is false as the voltage across the resistor is maximum at resonance.
Conclusion
From the analysis, the correct statements are:
- (a) Current is maximum at ω2=1LC
- (c) Voltage across R is maximum at ω2=1LC
Thus, the voltage statement is true for options (a) and (c).
---
In a series LCR circuit, resonance occurs when the inductive reactance (XL) equals the capacitive reactance (XC). This condition can be mathematically expressed as:
ω2=1LC
where ω is the angular frequency, L is the inductance, and C is the capacitance.
At resonance, the impedance of the circuit is minimized and is equal to the resistance R only. This results in the maximum current flowing through the circuit:
I=VR
where V is the voltage across the circuit. Therefore, the statement:
- (a) Current is maximum at ω2=1LC is true.
The statement:
- (b) Current is minimum at ω2=1LC is false because, as established, the current is maximum at this frequency.
At resonance, the voltage across the resistor VR is also at its maximum because the entire source voltage appears across the resistor when the circuit is in resonance. Therefore, the statement:
- (c) Voltage across R is maximum at ω2=1LC is true.
The statement:
- (d) Voltage across R is minimum at ω2=1LC is false as the voltage across the resistor is maximum at resonance.
From the analysis, the correct statements are:
- (a) Current is maximum at ω2=1LC
- (c) Voltage across R is maximum at ω2=1LC
Topper's Solved these Questions
Similar Questions
In a series LR circuit (L=3H,R=1.5Ω) and DC voltage =1V. Find current at T=2 seconds.
View SolutionIn series LCR circuit voltage leads the current. When
(Given that ω0 = resonant angular frequency)
View SolutionIn series LCR circuit, the voltages across R, L and C are shown in the figure. The voltage of applied source

View SolutionIn a series L−C circuit, the applied voltage is V0. if omega is very low, then the voltage drop across the inductor VL and capacitor VC are
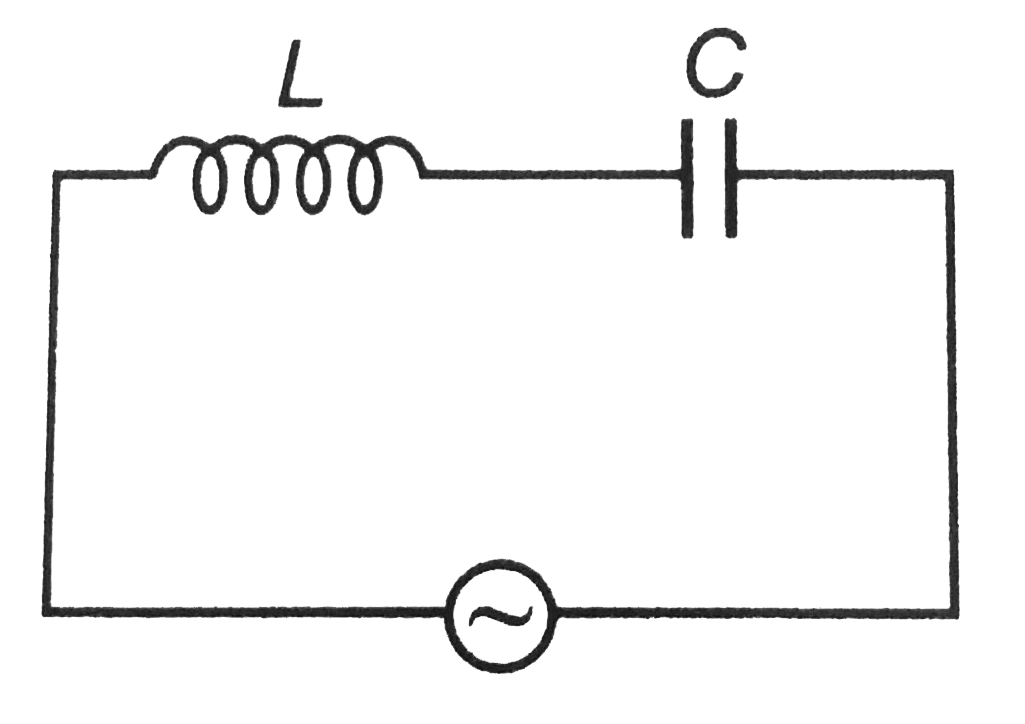 .
.
View SolutionIn a series LCR circuit resistance R=10Ω and the impedance Z=10Ω The phase difference between the current and the voltage is
View SolutionAC voltage source (V,ω) is applied across a parallel LC circuit as shown in figure. Find the impedance of the circuit and phase of current.
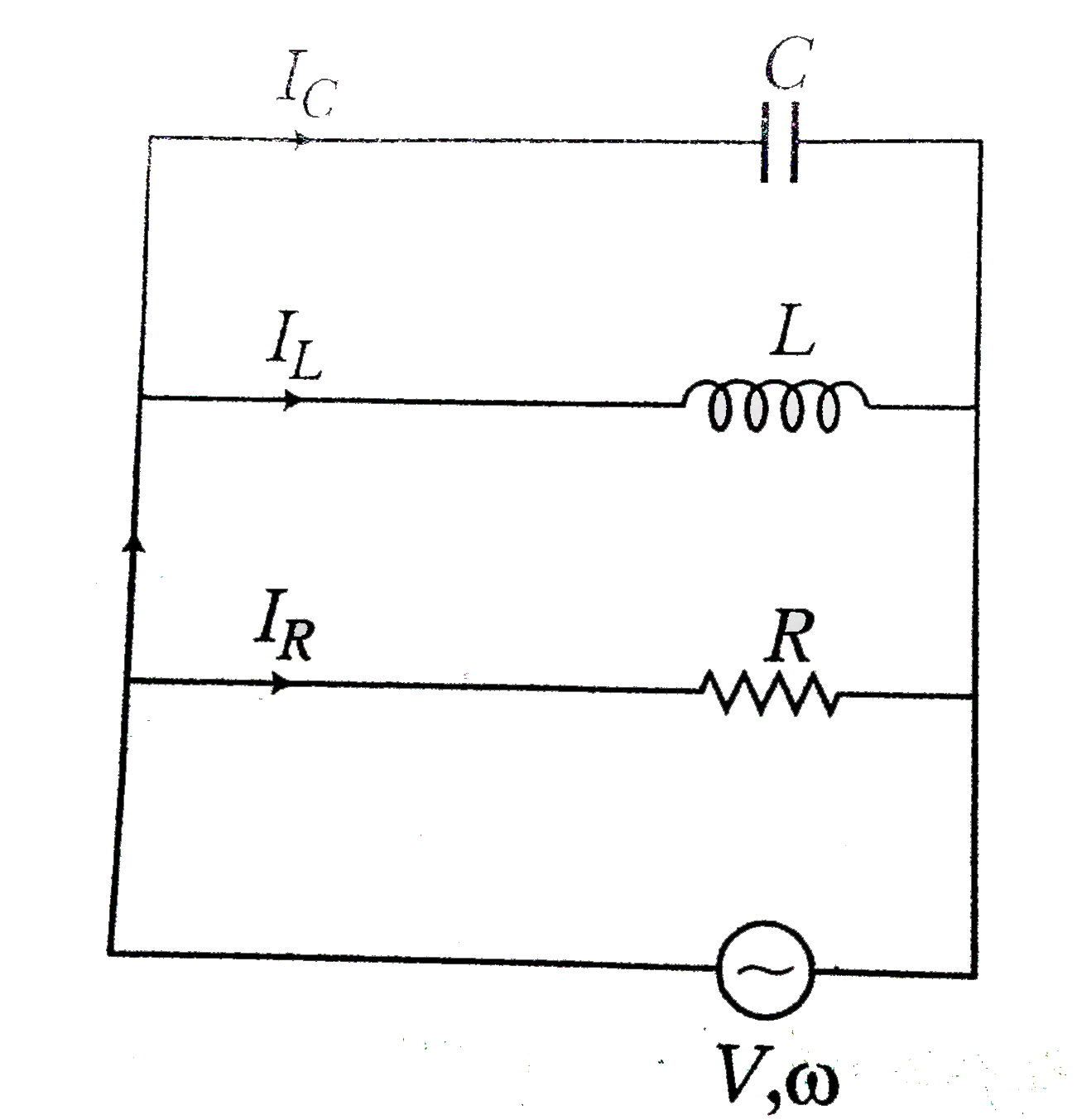
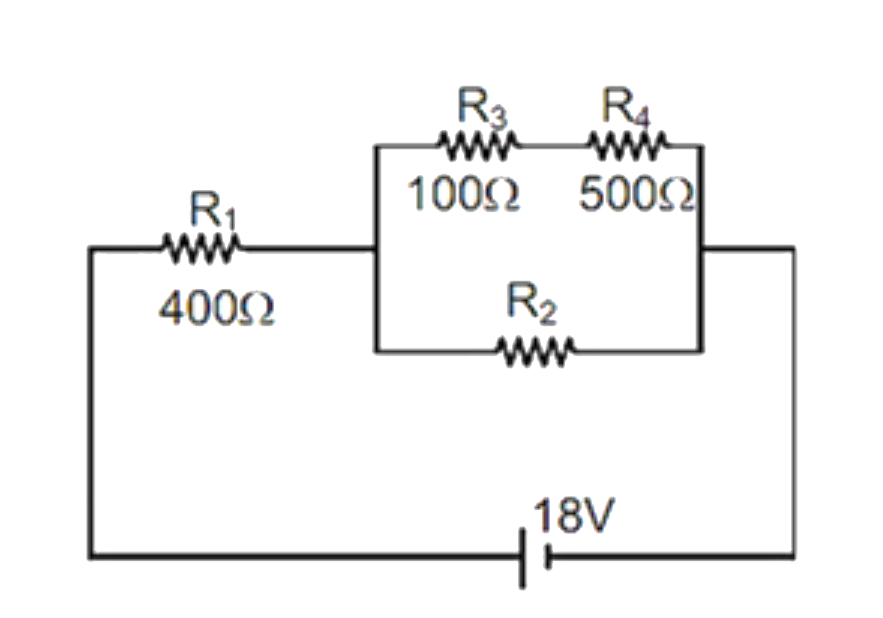
View SolutionIf the voltage across 500Ω is 5 V. then R2 is
View SolutionIn an LCR series ac circuit , the voltage across each of the components , L,C and R is 50 V . The voltage across the LC combination will be :
View SolutionIn a series resonant LCR circuit the voltage across R is 100 volts and R = 1k(Ω)withC=2(μ)F. The resonant frequency (ω) is 200rad/s. At resonance the voltage across L is
View SolutionIn an LCR series ac circuit the voltage across L,C and R are V1,V2 and V3 respectively The voltage of the source is .
View Solution
