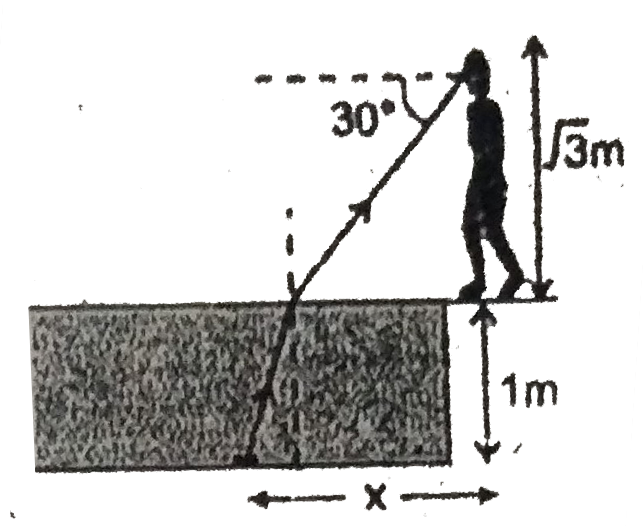
A man is standing at the edge of a 1m deep swimming pool, completely filled with a liquid of refractive index √32. The eyes of the man are √3m above the ground. A coin located at the bottom of the pool appears to be an angle of depression of 30∘ with reference to the eyes of man. Then horizontal distance (represented by x in the figure) of the coin from the eye of the man is ...........mm.
2000
3000
4000
8000
The correct Answer is:C
sin60∘=√32sinr
⇒r=45∘
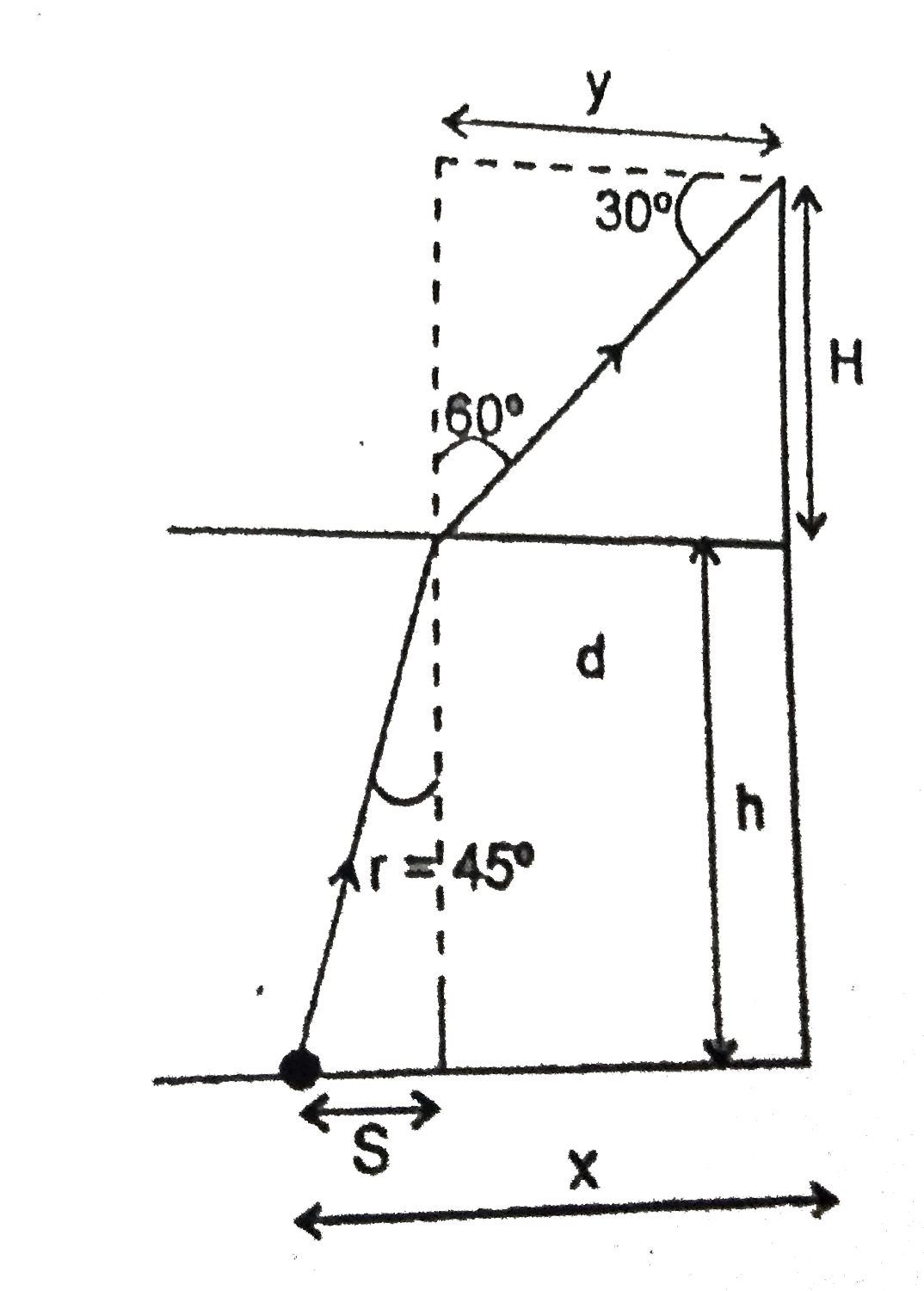
∴S=h=1m
y=Htan60∘=3m
∴x=S+y=4m=4000mm
Topper's Solved these Questions
Similar Questions
If there had been one eye of the man, then
View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View SolutionA coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View SolutionA certain prism of refracting angle 60∘ and of refractive index 2 is immersed in a liquid of refractive index √2 then the angle of minimum deviation will be
View SolutionA vessel of depth 2h is half filled with a liquid of refractive index 2√2 and the upper half with another liquid of refractive index √2. The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be:
View SolutionA man on the deck of a ship is 10m above the water level. He observes that the angle of elevation of the top of a cliff is 45o and the angle of depression of the base is 30o . Calculate the distance of the cliff from the ship and the height of the cliff.
View SolutionA man standing on the deck of a ship, which is 8m above water level. He observes the angle of elevation of the top of a hill as 60o and the angle of depression of the base of the hill as 30o . Calculate the distance of the hill from the ship and the height of the hill.
View SolutionA swimming pool is 18m long and 8m wide. Its deep and shallow ends are 2m and 1.2m respectively. Find the capacity of the pool, assuming that the bottom of the pool slopes uniformly.
View SolutionA man is moving away from a tower 41.6 m high at the rate of 2 m/sec. Find the rate at which the angle of elevation of the top of tower is changing, when he is at a distance of 30m from the foot of the tower. Assume that the eye level of the man is 1.6m from the ground.
View SolutionA man is moving away from a tower 41.6 m high at the rate of 2 m/sec. Find the rate at which the angle of elevation of the top of tower is changing, when he is at a distance of 30m from the foot of the tower. Assume that the eye level of the man is 1.6m from the ground.
View Solution

