The minimum sum of the distances of a real object and a real image from a concave mirror of radius of curvature 20cm is:
a.10 cm
b.40 cm
c.20 cm
d.none of these
The correct Answer is:B
To solve the problem of finding the minimum sum of the distances of a real object and a real image from a concave mirror with a radius of curvature of 20 cm, we can follow these steps:
1. Understand the relationship between radius of curvature and focal length:
The focal length (f) of a concave mirror is given by the formula:
f=R2
where R is the radius of curvature. Here, R=20cm, so:
f=202=10cm
2. Define object distance (u) and image distance (v):
For a concave mirror, the object distance (u) is taken as negative when the object is in front of the mirror. The image distance (v) is also negative for real images. We need to find the minimum value of |u|+|v|.
3. Use the mirror formula:
The mirror formula relates the object distance (u), image distance (v), and focal length (f):
1f=1v+1u
4. Express u in terms of v:
Rearranging the mirror formula gives:
1u=1f−1v
Therefore,
u=fvv−f
5. Find the sum of distances:
The sum of the distances can be expressed as:
S=|u|+|v|=−u−v
Substituting u from the previous step:
S=−(fvv−f)−v
6. Minimize the sum S:
To find the minimum sum, we can differentiate S with respect to v and set the derivative to zero. However, a simpler approach is to recognize that the minimum occurs when the object and image distances are equal in magnitude, i.e., |u|=|v|.
7. Set u = -v:
If we set |u|=|v|, then:
u=−v
Substituting into the mirror formula gives:
1f=1−v+1v
This leads to:
1f=0(which is not possible)
Instead, we can find the minimum sum by recognizing that the minimum occurs when both distances are equal to twice the focal length.
8. Calculate the minimum sum:
Since f=10cm, the minimum sum |u|+|v| occurs at:
|u|+|v|=2f+2f=4f=4×10=40cm
Final Answer:
The minimum sum of the distances of the real object and the real image from the concave mirror is:
40cm
The focal length (f) of a concave mirror is given by the formula:
f=R2
where R is the radius of curvature. Here, R=20cm, so:
f=202=10cm
For a concave mirror, the object distance (u) is taken as negative when the object is in front of the mirror. The image distance (v) is also negative for real images. We need to find the minimum value of |u|+|v|.
The mirror formula relates the object distance (u), image distance (v), and focal length (f):
1f=1v+1u
Rearranging the mirror formula gives:
1u=1f−1v
Therefore,
u=fvv−f
The sum of the distances can be expressed as:
S=|u|+|v|=−u−v
Substituting u from the previous step:
S=−(fvv−f)−v
To find the minimum sum, we can differentiate S with respect to v and set the derivative to zero. However, a simpler approach is to recognize that the minimum occurs when the object and image distances are equal in magnitude, i.e., |u|=|v|.
If we set |u|=|v|, then:
u=−v
Substituting into the mirror formula gives:
1f=1−v+1v
This leads to:
1f=0(which is not possible)
Instead, we can find the minimum sum by recognizing that the minimum occurs when both distances are equal to twice the focal length.
Since f=10cm, the minimum sum |u|+|v| occurs at:
|u|+|v|=2f+2f=4f=4×10=40cm
The minimum sum of the distances of the real object and the real image from the concave mirror is:
40cm
Topper's Solved these Questions
Similar Questions
What can be the largest distance of an image of real object from a convex mirror of radius of curvature is 20cm ?
View SolutionThe minimum distance between the object and its real image for concave mirror is
View SolutionFind the position, magnification and nature of the image of an object placed at a distance of 8 cm from a convex mirror of radius of curvature 24 cm.
View Solution
The distance between a convex lens and a plane mirror is 10 cm. The parallel rays incident on the convex lens after reflection from the mirror forms image at the optical centre of the lens. Focal length of lens will be
View SolutionThe minimum distance between an object and its real image formed by a convex lens is
View Solution(i) Calculate the distance of an object of height h from a concave mirror of radius of curvature 20 cm , so as to obtain a real image of magnification 2. find the location of image also .
(iii) Using mirror formula explain Why does a convex always produce a virtual image .
View SolutionThe co-ordinates of the image of point object P formed by a concave mirror of radius of curvature 20 cm (consider paraxial rays only ) as shown in the figure is
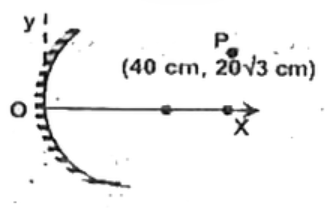
View SolutionA point object on the principal axis at a distance 1.5 cm in front of concave mirror of radius of curvature 20 cm has velocity 2mm/s is perpendicular to the principal axis. The velocity of image at that instant will be
View SolutionThe minimum distance between a real object and its real image formed by a thin converging lens of focal length f is
View SolutionThe image of a real object in a convex mirror is 4cm from the mirror. If the mirror has a radius of curvature of 24cm, Find the position of object and magnification
View Solution
