A radioactive with half life T=693.1 days. Emits β-particles of average kinetic energy E=8.4×10−14 joule. This radionuclide is used as source in a machine which generates electrical energy with efficiency η=12.6%. Number of moles of the nuclide required to generate electrical energy at an initial rate is P=441KW, is n×10n then find out value of nm(loge2=0.6931)NA=6.023×1023
The correct Answer is:2
To solve the problem step by step, we will follow the outlined reasoning from the video transcript and derive the necessary equations to find the required values.
Step 1: Calculate the Decay Constant (λ)
The decay constant (λ) can be calculated using the half-life (T) of the radioactive substance:
λ=ln(2)T
Given that T=693.1 days, we need to convert this into seconds:
T=693.1×24×3600 seconds
Calculating this gives:
T=693.1×86400=59719680 seconds
Now substituting into the decay constant formula:
λ=0.693159719680≈1.16×10−9 s−1
Step 2: Determine the Activity (A)
The activity (A) of the radioactive substance is given by:
A=λN
Where N is the number of atoms. The number of moles (n) is related to N by:
N=n×NA
Where NA=6.023×1023 is Avogadro's number. Thus, we can write:
A=λ(n×NA)
Step 3: Calculate the Power Input (P_input)
The power input to the machine can be expressed as:
Pinput=A×E
Where E=8.4×10−14 joules is the average energy emitted per decay. Substituting for A:
Pinput=λ(n×NA)×E
Step 4: Relate Output Power and Efficiency
The efficiency (η) is given as:
η=PoutputPinput
Given Poutput=441 kW=441×103 W, we can rearrange this to find Pinput:
Pinput=Poutputη=441×1030.126
Calculating this gives:
Pinput≈3500000 W (or 3.5×106 W)
Step 5: Substitute and Solve for n
Now we can set the two expressions for Pinput equal to each other:
λ(n×NA)×E=3.5×106
Substituting the values we have:
(1.16×10−9)(n×6.023×1023)(8.4×10−14)=3.5×106
Calculating the left side:
(1.16×10−9)(6.023×1023)(8.4×10−14)≈5.87×101n
Setting this equal to 3.5×106:
5.87×101n=3.5×106
Solving for n:
n≈3.5×1065.87×101≈5960≈6×103
Step 6: Find n and m
From the problem, we have n=6 and m=3 (since n×10m implies m is the exponent).
Step 7: Calculate the Ratio nm
Finally, we need to find the ratio:
nm=63=2
Final Answer
Thus, the value of nm is:
2
The decay constant (λ) can be calculated using the half-life (T) of the radioactive substance:
λ=ln(2)T
Given that T=693.1 days, we need to convert this into seconds:
T=693.1×24×3600 seconds
Calculating this gives:
T=693.1×86400=59719680 seconds
Now substituting into the decay constant formula:
λ=0.693159719680≈1.16×10−9 s−1
The activity (A) of the radioactive substance is given by:
A=λN
Where N is the number of atoms. The number of moles (n) is related to N by:
N=n×NA
Where NA=6.023×1023 is Avogadro's number. Thus, we can write:
A=λ(n×NA)
The power input to the machine can be expressed as:
Pinput=A×E
Where E=8.4×10−14 joules is the average energy emitted per decay. Substituting for A:
Pinput=λ(n×NA)×E
The efficiency (η) is given as:
η=PoutputPinput
Given Poutput=441 kW=441×103 W, we can rearrange this to find Pinput:
Pinput=Poutputη=441×1030.126
Pinput≈3500000 W (or 3.5×106 W)
Now we can set the two expressions for Pinput equal to each other:
λ(n×NA)×E=3.5×106
Substituting the values we have:
(1.16×10−9)(n×6.023×1023)(8.4×10−14)=3.5×106
Calculating the left side:
(1.16×10−9)(6.023×1023)(8.4×10−14)≈5.87×101n
Setting this equal to 3.5×106:
5.87×101n=3.5×106
Solving for n:
n≈3.5×1065.87×101≈5960≈6×103
From the problem, we have n=6 and m=3 (since n×10m implies m is the exponent).
Finally, we need to find the ratio:
nm=63=2
Thus, the value of nm is:
2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise-2 Part-3 One more than one options correct type7videos
NUCLEAR PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise-2 Part-4 Comprehension6videos
NUCLEAR PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise 2 Part-1 Only one option correct type20videos
NUCLEAR PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS16videos
GRAVITATION
- BOOK - RESONANCE ENGLISHCHAPTER - REVISION DPPEXERCISE - All Questions463videos
REVISION DPP
Similar Questions
A radio nuclide with half life T=69.31 second emits β-particles of average kinetic energy E=11.25eV. At an instant concentration of β-particles at distance, r=2m from nuclide is n=3×1013 per m3.
(i) Calculate number of nuclei in the nuclide at that instant.
(ii) If a small circular plate is placed at distance r from nuclide such that β-particles strike the plate normally and come to rest, calculate pressure experienced by the plate due to collision of β-particle. (Mass of β-particle =9×10−31kg) (loge2=0.693)View SolutionThe average kinetic energy of one molecule of an ideal gas at 27∘C and 1 atm pressure is [Avogadro number NA=6.023×1023 ]
View SolutionCalculate the average kinetic energy of oxygen molecule at 0∘C. (R=8.314Jmol−1 K−1,NA=6.02×1023)
View SolutionThe width of depletion region in p-n junction diode is 500nm and an intrinsic electric field of 6×105Vm−1 is also found to exist in it. What is the kinetic energy which a conduction electron must have in order to diffuse from the n-side to p-side?
View SolutionFor a first order reaction, rate constant is given is logk=14−1.2×104T, then what will be value of temperature if
its half life period is 6.93×10−3min ?View SolutionAn electromagnetic wave of frequency 1×1014 Hertz is propagating along z-axis. The amplitude of electric field is 4V/m. If ε0=8.8×10−12C2/N−m2, then average energy density of electric field will be:
View SolutionAn electromagnetic wave of frequency 1×1014 Hertz is propagating along z-axis. The amplitude of electric field is 4V/m. If ε0=8.8×10−12C2/N−m2, then average energy density of electric field will be:
View SolutionThere is uniformly charged disc of surface charge density σ and of radius 1m. H=10m height below the disc is a gun which is continuously emitting a charged particle and its isotopic in the vertically upward direction. The particles are charged through same potential before being emitted. The charge of the particle is q=8×10−19C. The difference of potential energies of particle and the isotopic at B is 10−23Joule. Also the velocity of the particle at B is zero. The ratio of masses of particle and isotopic is 32. If the total energy of isotope at B is 1.1k×10−23J Then find k..(Given σ/ε0=10−4N/C).
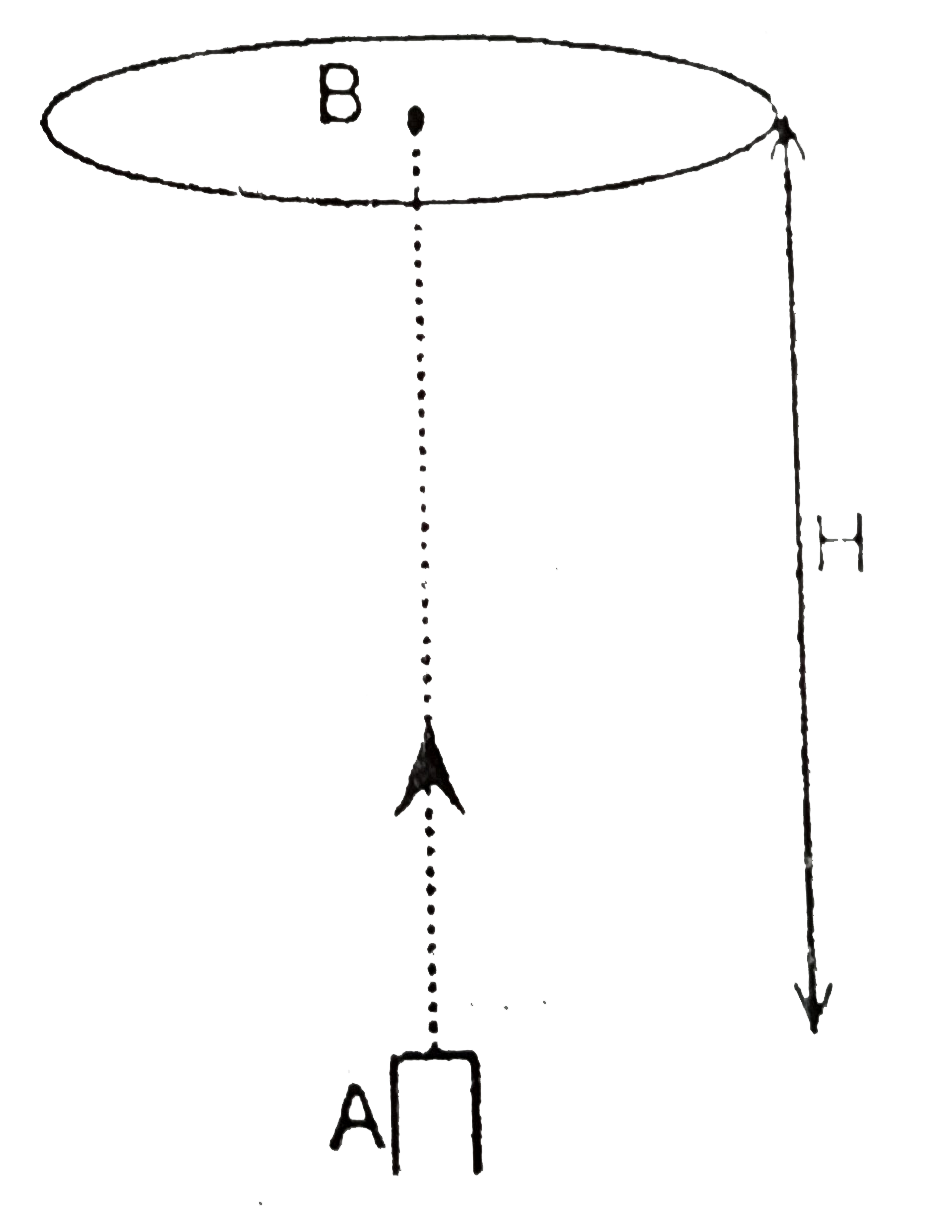 View Solution
View SolutionAn α−particle is describing a circle of radius 0.45 m in a field of magnetic induction of 1.2 T. Find its speed, frequency of rotation and kinetic energy. What potential difference will be required to accelerate the particle so as to give this much of the energy to it? The mass of α−particle is 6.8×10−27kg and its charge is twice the charge of proton, i.e.,3.2×10−19C.
View SolutionA metal wire having Poisson's ratio 14 and Young's modulus 8×1010N/m2 is stretched by a force, which produces a lateral strain of 0.02% in it. The elastic potential energy stored per unit volume in wire is [in Jm3']
View Solution

