An ideal gas expands from V to 2V in 4 separate processes. Where process 1 is isothermal process 2 is adiabatic, process 3 is free expansion and process 4 is isobaric. If E1,E2,E3 and E4 are the changes in average kinetic energy of the molecules in the isothermal, adiabatic free expansion and isobaric process respectively then choose the correct options.
E2=E3
E1=E3
E1>E4
E4>E3
The correct Answer is:B, D
To solve the problem, we need to analyze the four processes of the ideal gas expansion and determine the changes in average kinetic energy (E1, E2, E3, and E4) for each process.
1. Isothermal Process (Process 1):
- In an isothermal process, the temperature (T) of the gas remains constant.
- The change in average kinetic energy (E1) is given by the formula:
E1=32kBΔT
- Since there is no change in temperature (ΔT = 0), we have:
E1=0
2. Adiabatic Process (Process 2):
- In an adiabatic process, there is no heat exchange with the surroundings (Q = 0).
- The work done on/by the gas results in a change in internal energy, which is related to temperature change.
- Since the gas expands, it does work on the surroundings, which decreases its internal energy and thus decreases the temperature.
- Therefore, the change in average kinetic energy (E2) will be negative:
E2<0
3. Free Expansion (Process 3):
- In free expansion, the gas expands into a vacuum without doing work and without heat exchange.
- There is no change in temperature (ΔT = 0), so:
E3=32kBΔT=0
4. Isobaric Process (Process 4):
- In an isobaric process, the pressure remains constant.
- As the volume increases, the temperature must also increase (from the ideal gas law: PV = nRT).
- Thus, the change in average kinetic energy (E4) will be positive:
E4=32kBΔT(ΔT>0)
Summary of Results:
- E1=0 (Isothermal)
- E2<0 (Adiabatic)
- E3=0 (Free Expansion)
- E4>0 (Isobaric)
Conclusion:
- From the analysis, we can conclude:
- E1=E3=0
- E2<0
- E4>0
Correct Options:
1. E1=E3 (True)
2. E2<E3 (True, since E2<0 and E3=0)
3. E1>E4 (False, since E1=0 and E4>0)
4. E4>E3 (True, since E4>0 and E3=0)
Final Choices:
- The correct options are: E1=E3, E2<E3, and E4>E3.
- In an isothermal process, the temperature (T) of the gas remains constant.
- The change in average kinetic energy (E1) is given by the formula:
E1=32kBΔT
- Since there is no change in temperature (ΔT = 0), we have:
E1=0
- In an adiabatic process, there is no heat exchange with the surroundings (Q = 0).
- The work done on/by the gas results in a change in internal energy, which is related to temperature change.
- Since the gas expands, it does work on the surroundings, which decreases its internal energy and thus decreases the temperature.
- Therefore, the change in average kinetic energy (E2) will be negative:
E2<0
- In free expansion, the gas expands into a vacuum without doing work and without heat exchange.
- There is no change in temperature (ΔT = 0), so:
E3=32kBΔT=0
- In an isobaric process, the pressure remains constant.
- As the volume increases, the temperature must also increase (from the ideal gas law: PV = nRT).
- Thus, the change in average kinetic energy (E4) will be positive:
E4=32kBΔT(ΔT>0)
- E1=0 (Isothermal)
- E2<0 (Adiabatic)
- E3=0 (Free Expansion)
- E4>0 (Isobaric)
- From the analysis, we can conclude:
- E1=E3=0
- E2<0
- E4>0
1. E1=E3 (True)
2. E2<E3 (True, since E2<0 and E3=0)
3. E1>E4 (False, since E1=0 and E4>0)
4. E4>E3 (True, since E4>0 and E3=0)
- The correct options are: E1=E3, E2<E3, and E4>E3.
Similar Questions
A gas is expanded from volume V0=2V0 under three different processes. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gas in these three processes. then
 View Solution
View SolutionAn ideal gas may expands from V0 to 2V0 according to following three processes. Molar specific heat for processes b will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gas in these three processes then
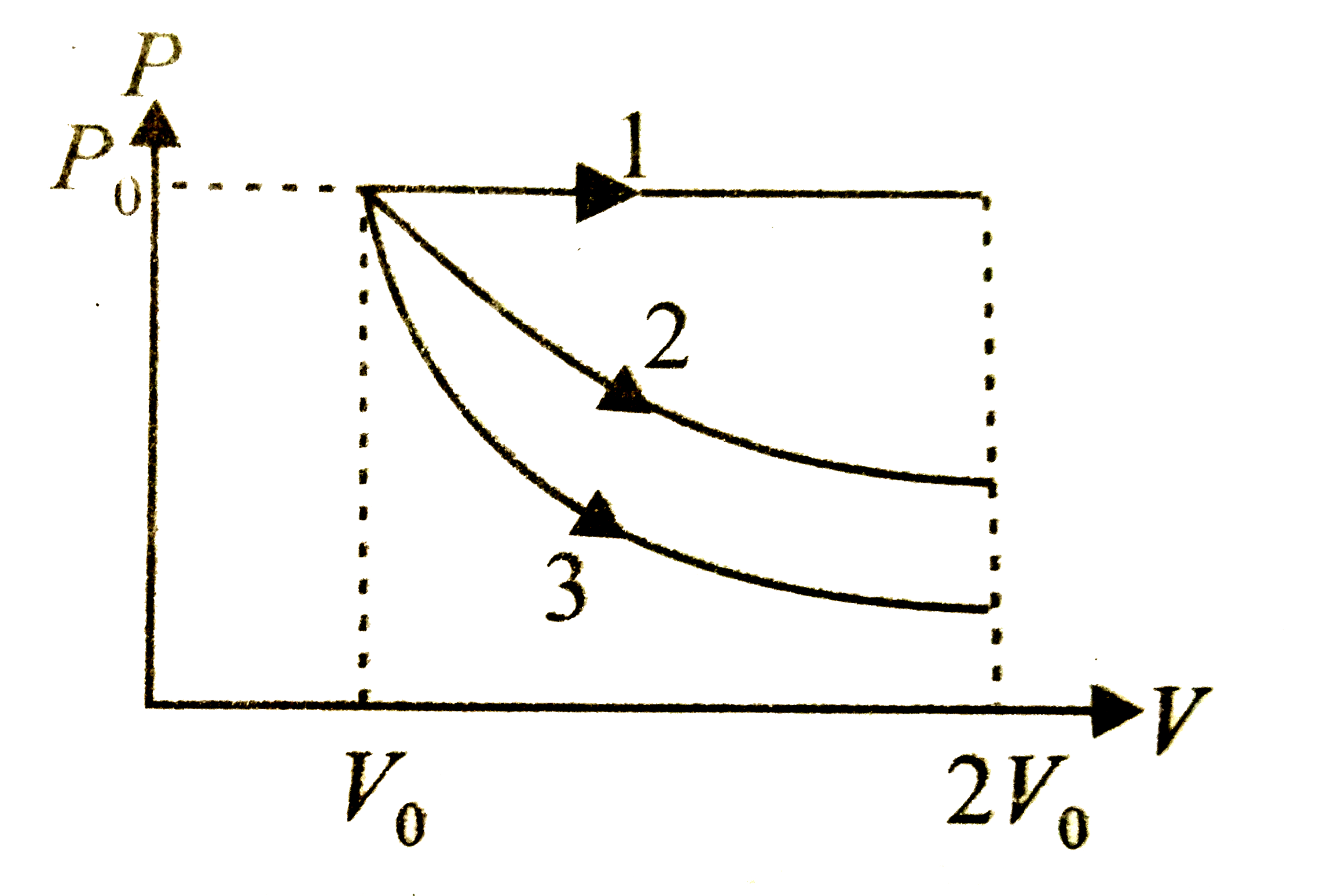 AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
If w1,w2,w3 and w4 for an ideal gas are magnitude of work done in isothermal, adiabatic, isobaric and isochoric reversible expansion processes, the correct order will be :
View SolutionIf w1.w2,w3 and w4 are work done in isothermal, adiabatic, isobaric, and isochoric reversible expansion for an ideal gas, respectively, then
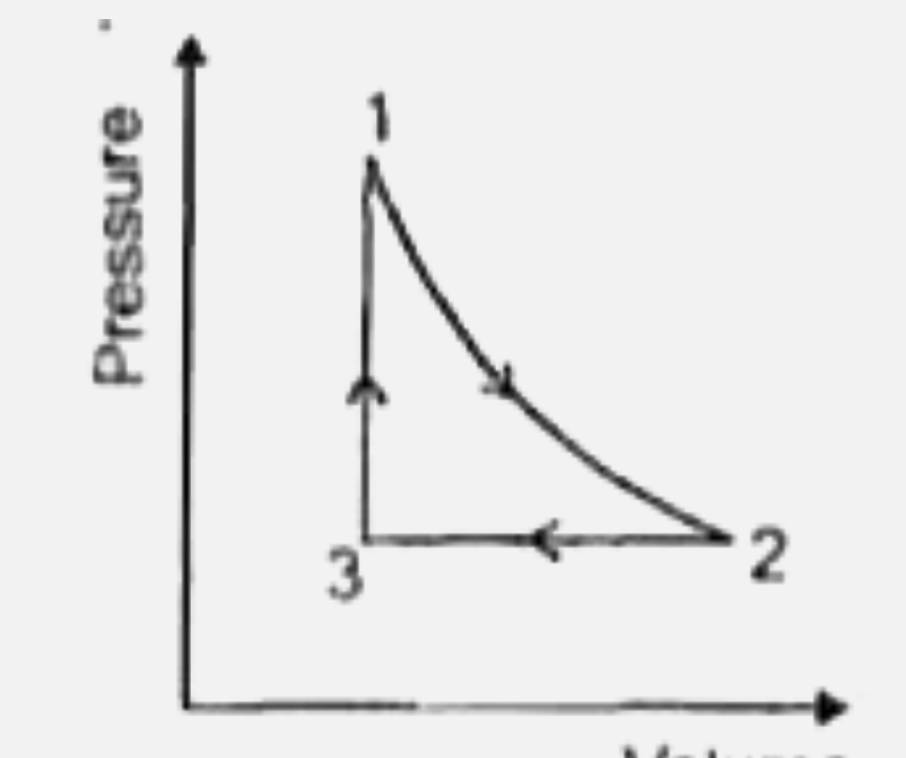
View SolutionGiven here is a cyclic process on P -V diagram. Process 1-2 is isothermal, 2-3 is isobaric and 3-1 is an isochoric process. Plot this T - P diagram.
 View Solution
View Solution
An ideal gas undergoes a cyclic process, in which one process is isochoric, one process is isothermal and one process is adiabatic. During the isothermal process, 40 J heat is released by the gas, and during the isochoric process, 80 J heat is absorbed by the gas. if work done by the gas during adiabatic process is W1 and during isothermal process is W2 then the magnitude of W1W2 will be equal to:View SolutionTemperature of a monoatomic gas is increased from T0 to 2T0 in three different processes:
isochoric, isobaric and adiabatic. Heat given to the gas in these three processes are Q1,Q2andQ3 respectively. Then, choose the correct option.View Solution
n moles of a monoatomic gas undergoes a cyclic process ABCDA as shown. Process AB is isobaric, process BC is adiabatic process CD is isochoric and process DA is isothermal the maximum temperature and minimum temperature in cycle are 4T0 and T0 respectively. Then:View Solution
n moles of a monoatomic gas undergoes a cyclic process ABCDA as shown. Process AB is isobaric, process BC is adiabatic process CD is isochoric and process DA is isothermal the maximum temperature and minimum temperature in cycle are 4T0 and T0 respectively. Then:View Solution

